Bias in Rendering
Àâòîð: Keenan Crane
Èñòî÷íèê: http://multires.caltech.edu/~keenan/bias.pdf
Àâòîð: Keenan Crane
Èñòî÷íèê: http://multires.caltech.edu/~keenan/bias.pdf
Unbiased and consistent are two terms people use to describe error in a rendering algorithm. Although the exact behavior of error might not appear interesting, it has a large impact on how easy the method is to use and how robust it is (in other words, how well it works with a large variety of scenes).
Some people prefer unbiased methods because they make it easy to put a bound on the error. Having a good estimate of the error makes it easier to know when more computation is needed. It can also mean that fewer parameters need to be adjusted in order to produce a good-looking image.
On the other hand, biased methods tend to be much more efficient for common scenes than unbiased methods. These methods make reasonable simplifying assumptions which improve efficiency. For example, an algorithm might assume that all indirect illumination has low spatial frequency and therefore estimate indirect bounces by interpolating among a small set of samples. However, since error bounds for unbiased methods are generally unknown it is often difficult to pick parameters which correspond to the desired level of quality.
Overall there is a tradeoff between fast, biased methods and robust, unbiased methods. However, there is no hard evidence that unbiased algorithms must be slow or that biased algorithms cannot be robust. The vast majority of commercial applications use fast approximations (rasterization and REYES) which are neither unbiased nor consistent, nor robust!

Figure 1: Both biased (dark gray) and unbiased (light gray) methods can be consistent, but the error in an unbiased method is always predictable. Many popular methods (black) converge to the wrong answer very quickly!
People often confuse the term unbiased with the term consistent; for example, you may hear someone say (incorrectly), “photon mapping is unbiased since it converges to the correct solution.” These two terms have two precise and different meanings, and it is important to understand the difference.
Consistency is easy to understand: if an approximation approaches the correct solution as computation time increases, then the method is consistent. However, merely knowing that a method is consistent tells you very little. For instance, it does not tell you how quickly the method converges to the correct solution, nor does it give any bound on the error. In general, an estimator FN for a quantity I is consistent for E if
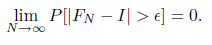
In other words, as we take more samples, the probability of the error being greater than some fixed value E approaches zero. Most often, “consistent” just means E = 0, i.e., the estimator approaches the exact answer.
Bias is slightly subtler: a method is unbiased if it produces the correct answer on average. An easy way to think about bias in rendering is to ask, “if I rendered the same image millions of times using different random numbers, would averaging the results give me the right answer?” If the answer is “no,” you probably have a biased algorithm.
Formally, an estimator is unbiased if

that is, the expected error or bias is equal to zero – regardless of the value of N. An image path traced with only one sample per pixel is still an unbiased estimate of the correct image, because if you averaged millions of 1-sample path-traced images you’d get the right answer. For an unbiased method, the error is proportional to the variance of the estimator, which is equal to 1/N Var[f], where f is the integrand.
There are many potential sources for bias. A rendering algorithm is usually biased because it ignores some type of lighting effect, it misrepresents the contributions of various lighting effects to the image, or it simply computes some quantity of light inaccurately. Most methods are biased because they ignore certain classes of light paths (e.g., light which bounces off mirrors or is focused through glass). In this case, the result is darker than the correct image, and may lack important visual cues. Real time methods often skip visibility calculations required for correct shadowing, yielding a result which is too bright. Other methods introduce bias by interpolating among a sparse set of sample values, ignoring high-frequency features and giving the image a blurry appearance. Geometric aliasing (e.g., approximating a smooth surface with triangles) may also appear to be a source of bias. However, when analyzing rendering algorithms we assume that the scene as described is the one we want to render, and focus on error due to the way light transport is handled, i.e., how light is scattered and propagated through the scene.

Figure 2: Left: light paths which bounce multiple times before reaching the eye were omitted. Right: Such paths can be very illuminating...
There are very few rendering algorithms which are completely unbiased: even path tracing, which is generally a robust algorithm, ignores several types of light paths. Below are some of the most popular rendering algorithms and their respective sources of error. Various types of light paths are specified using Heckbert’s regular expression notation where L is a point on a light source, E is the eye, D is a diffuse bounce, S is a specular bounce, and “*” means “zero or more.”
| method | unbiased | consistent | notes |
| radiosity | Standard radiosity takes into account only paths of the form LD * E – light bounced diffusely from one surface to another until it hits the eye. Additionally, irradiance is computed over a coarse grid which does not properly capture occlusion (shadows). Although the latter source of error disappears as grid resolution increases, radiosity will always neglect certain types of light paths. Therefore, it is not consistent. | ||
| path tracing | + | + | Path tracing is usually an accurate way to compute a reference image, but there are a few pathological cases where it will fail. (See [Veach], pp 237-240 for further discussion.) |
| bidirectional path tracing | + | + | By connecting subpaths starting from both the eye and the light, bidirectional path tracing avoids the cases which prevent standard path tracing from being unbiased. |
| Metropolis light transport | + | + | Since MLT uses an ergodic set of mutation rules (and because care is taken to avoid startup bias), it is unbiased. In other words, as long as we’re able to explore all paths which could potentially carry light, detailed balance guarantees that we will converge to the correct answer. |
| photon mapping | + | There are several sources of bias in photon mapping, but to see that it is biased simply consider what happens when a large number of images generated by a photon mapper are averaged. For example, if we have too few photons in the caustic map, caustics appear blurry due to interpolation. Averaging a large number of blurry caustics will not result in a sharp caustic – in other words, we don’t expect to get the correct answer on average. On the other hand, as we increase the number of photons in the photon map, the region used for each density estimate shrinks to a point. In the limit, a photon used to estimate illumination at a point will correspond to the end of a light subpath at that point. Therefore, as long as the photon map contains a proper distribution of paths, photon mapping is consistent. | |
| rasterization | Most real-time rendering is done using an API such as OpenGL or DirectX which performs all shading based on the information passed to each triangle by a rasterizer. Traditionally, this framework was limited to integration of paths of the form LDE – paths which bounce off a single diffuse surface before hitting the eye. More recent programmable graphics cards can render a larger variety of phenomena, but these are still typically gross approximations of true light transport calculations. Therefore, most images produced via rasterization will not produce the correct solution, regardless of the level of quality. Modern real-time APIs are a mutant example of the tradeoff between speed and robustness: nearly any effect can be achieved in real-time, at the cost of highly special-purpose algorithms. |
Consider a scene where we have an immensely powerful light source in one room and a camera in an adjacent room, where the two rooms are connected only by a microscopic hole (as pictured below). Even with the most efficient rendering algorithm, it may take hundreds of thousands of samples to find a path which connects the light to the camera. If our stopping criterion is a function of our sample variance, we will stop long before we find such a path, since we cannot accurately estimate the constant in our error term. However, we can always make the light bright enough that it will have a substantial effect on the visible illumination. In general, guaranteeing that an image is correct is more difficult than simply finding an unbiased algorithm.
