Кремер Е. - Рекурсивный расчет нетто-премии для крупнейших исков перестраховочной защиты

Аннотация

Кремер Е. Рекурсивный расчет нетто-премии для крупнейших исков перестраховочной защиты В данной работе автор исследует проблему расчета нетто-премии для некоторых вариантов крупнейших исков перестрахования. Очень удобным методом является рекурсивный метод оценки, полученный путем применения некоторых рекуррентных формул для ожидания порядковых статистик.

1. Введение

Расчет премии для договора при страховании является очень старой и основной проблемой в непропорциональном виде перестрахования. Математические оценочные методы для классических stop-loss и excess-of-loss договоров уже представлены Helbig (1953) и Ammeter (1955). Альтернативой договора excess-of-loss, так называемый ECOMOR-договор был исследован французским актуарием Thepaut (1950), в то время как более знакомое понятие крупнейших исков перестраховочных договоров пришло в употребление не ранее, чем в 1964 году (Ammeter 1964).

Несколько лет назад автор настоящей работы рассматривал проблему расчета премии за последние два договора, вдохновленный статьей Benktander (1978). Результаты, представленные в семи работах (Кремер 1982, 1983, 1984а, b, 1985a, b), были переработаны и обобщены для договоров с применением результатов теории порядковых статистик. Формулы общей премии были доказаны (см. 1982 Кремер, 1983, 1984b). В настоящей работе расчет нетто-премии повторно исследуется для обобщения крупнейших исков, и доказательства теоремы, позволяющей путем применения простых рекурсивных расчетов для определения нетто-премии. Настоящая статья является в некотором смысле аналогом предыдущей Panjer (1981), с указанием того, что метод рекурсивного расчета нетто-премии применяется для договора stop-loss.

2. Перестраховочная защита

Рассмотрим К коллективных рисков и пусть N является случайной величиной обозначающей количество исков. Соответствующий иск описывается переменными Х₁, Х₂, …, Х_n. Учтем, что:

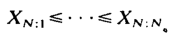
иски упорядочены по возрастанию. Пусть с₁, с₂, …, с_р константы, которые определены для заданного натурального числа р

описывает сумму, уплаченную перестраховщиком. Следовательно, вектор (с₁, с₂, …, с_р) определяет договор перестрахования и называется обобщенным покрытием крупнейших исков (сокращенно: LCR (с₁, с₂, …, с_р)).

В особых случаях:

(а) с₁=с₂=…=с_р=1 классический договор крупнейших исков, покрывающий р крупнейших исков.

(b) с₁=с₂=…=с_р-1=1, с_р=(1-р) классический ECOMOR-договор, покрывающий все иски сверх р крупнейшего иска.

Пусть:

нетто-премия LCR (с₁, с₂, …, с_р) договора. Если предположить, что параметры иска Х₁, Х₂, … должны быть независимы и одинаково распределены, с непрерывной функцией распределения и независимой из N, то имеет место (см. Кремер 1985a)

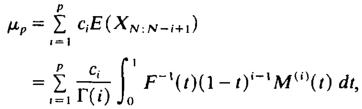Нетто-премия (2.1)

где:

это псевдо обратная функция распределения размера иска и M⁽ⁱ⁾ – i-ая производная момента генерирующей функции

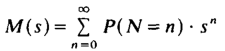
N-ых исков. Таким образом, с теоритической точки зрения нет никаких проблем при расчете нетто-премии μ_p. Но с эмпирической точки зрения, приведенный выше результат не удовлетворяет, так как необходимо оценить F, а также M⁽ⁱ⁾(s), i=1,…,р из известных прошлых размеров исков и номеров. Это привело к разработке различных более удобных подходов к оценке μ_p. Кроме прямой оценки μ_p статистическими методами, особенно так называемыми процедурами сжигания стоимости, актуарии думали о получении простого верхнего предела μ_p (см. Benktander 1978, Кремер 1983), который становится асимптотически точным (см. Кремер 1982). В следующем разделе предложен другой подход, который позволяет определить нетто-премию методом простых рекурсивных расчетов.

3. Рекурсивная оценочная процедура

Мы рассмотрим распределение семейства исков, удовлетворяющих рекурсии

где

Особые случаи распределения Пуассона, биномиального распределения, отрицательного биномиального распределения и геометрического распределения (см. Panjer 1981). Характеристику распределения следуя приведенной выше рекурсии приведено в Sundt и Jewell (1981).

Первый шаг для получения рекурсивного метода расчета премии может рассматриваться простым уравнением:

Теорема. Предположим, что размеры иска одинаково распределены и вероятности их числа μ_p, μ_p-1, μ_p-2 с учетом приведенной выше рекурсии. Затем для чистых премий страховых договоров LCR(с₁, с₁, …, с_р), LCR(с₁, с₁, …, с_р-1), LCR(с₁, с₁, …, с_р-2) рекурсия

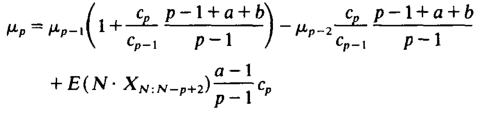
начиная с

μ_i^*– среднее значение i-го иска:

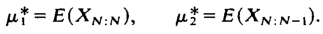
4. Пример

Пусть a, b произвольные, но c_p=c_p-1,

Для договора в общем

Нетто-премия для договора в общем 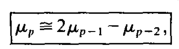(4.1)

который является очень привлекательным с практической точки зрения.

Сравним это с рекурсией премии рассчитываемой по формуле (2.1) в случае λ=100 и

(а) Для размера иска функции распределения Парето:

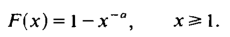
Функция распределения Парето для размера иска

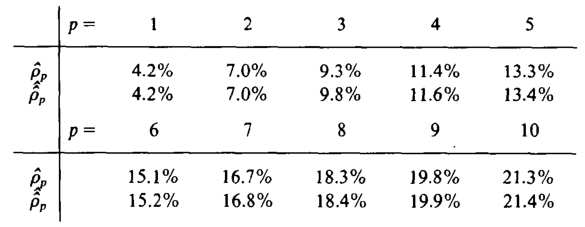
Обозначим через μ_p нетто-премию, которая рассчитывается по формуле

которая, как известно, обладает очень хорошим приближением к μ_p (см. Ammeter 1964). Наконец, определим 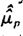Нетто-премия 2 , нетто-премия рассчитывается по высшей рекурсии. При средней сумме исков

каждый получает ставки страховых взносов

Таблицы ставок при разных значениях альфа

(b) Для экспоненциальной функции распределения

Обозначим через 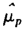Нетто-премия 1 нетто-премию, которая рассчитывается по формуле:

Ставки премий и чаевых определены выше.

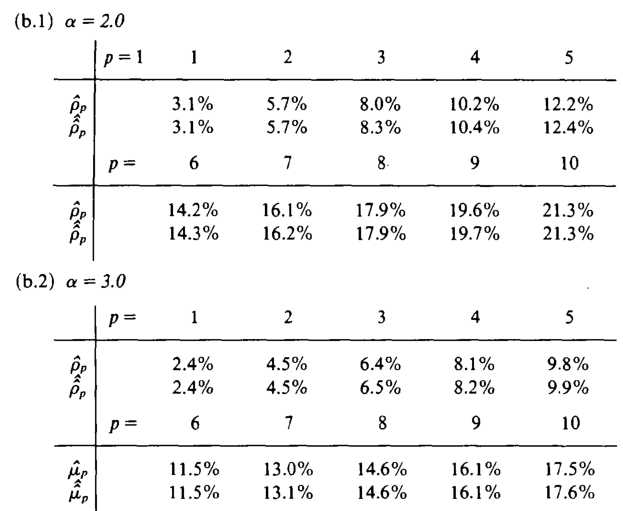
В соответствии с этими результатами рекурсий (4.1) может в полной мере быть рекомендован для практического применения оценки нетто-премии. Обратите внимание, что это дает очень простой и быстрый метод оценки премии классической крупнейших исков при р> 2, зная только оценки для ожидания первого и второго по величине исков страхового портфеля. В обоих примерах исходные значения могут быть рассчитаны по результатам AMMETER (1964).

Литература

1. AMMETER, H. (1955) The Calculation of Premium Rates for Excess of Loss and Stop Loss Reinsurance Treaties. Nonproportional Reinsurance. Bruxelles, pp. 79-109.
2. AMMETER, H. (1964) The Rating of "Largest Claim" Reinsurance Covers. Quarterly letter from the Allgemeene Reinsurance Companies, Jubilee number 2, pp. 5-17.
3. BENKTANOER, G. (1978) Largest Claims Reinsurance (LCR): A Quick Method to Calculate LCR-Risk Rates from Excess of Loss Risk Rates. ASTIN Bulletin, 54-58.
4. DaviD, H.A. (1980) Order stalistics. John Wiley, New York. H ELBIG, M. (1953) Mathematische Grundlagen der Schadenexzedenten-riickversicherung. Festschrift flir Emil Bebler, 189-197.
5. JOHNSON, N.I. and KOTZ, S. (1969) Discrete distributions. John Wiley, New York. KREMER, E. (1982) Rating of Largest Claims and ECOMOR Reinsurance Treatise for Large Portfolios. ASTIN Bulletin, 47-56.
6. KREMER, E. (1983) Distribution-Free Upper Bounds on the Premiums of the LCR and ECOMOR Treaties. Insurance: Mathematics and Economics, 209-213.
7. KREMER, E. (1984a) Rating of Nonproportional Reinsurance Treatise Based on Ordered Claims. Premium Calculation in Insurance. Proceedings of the NATO Advanced Study Institute, Leuven, pp. 285-314.
8. KREMER, E. (1984b) An Asymptotic Formula for the Net-Premium of some Reinsurance Treaties. Scandinavian Actuarial Journal, 11-22.
9. KREMER, E. (1985a) Finite Formulae for the Premium of the General Reinsurance Treaty Based on Ordered Claims. Insurance: Mathematics & Economics, 233-238.
10. KREMER, E. (1985b) Reinsurance Premiums Under Special Claims Number Distribution. Submitted for publication.
11. KREMER, E. (1986) Simple Formulas for the Net Premiums of the LCR and ECOMOR Treaties Under Exponential Claims Sizes. BIfitter der Deutschen Gesellschaft fiir Versicherungs mathematik.
12. SUNDT, B. and JEWELL, W.S. (1981) Further Results on Recursive Evaluation of Compound Distributions. ASTIN Bulletin, 27-30.
13. PANJER, H.H. (1981) Recursive Evaluation of a Family of Compound Distributions. ASTINBuUetin, 22-26.
14. THЕPAUT, A. (1950) Le Trait d'Exc6dent du Cofit relativ., Bulletin Trimestriel de L'Institut des Actuaries Francais, No. 2.