Понижение энергопотребления сенсорных сетей за счет предварительной обработки данных
Авторы: Е.Г. Краморенко, М.В. Привалов
Описание: Выполнен анализ методов предварительной обработки и компрессии числовых данных. Произведен анализ результатов их применения в сенсорных сетях для понижения энергопотребления. Выбраны наиболее перспективные алгоритмы.
Источник: Информационные управляющие системы и компьютерный мониторинг 2013/ Сборник материалов к IV Всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых. — Донецк, ДонНТУ — 2013, с. 364 — 369.
Аннотация
Краморенко Е.Г., Привалов М.В. Понижение энергопотребления сенсорных сетей за счет предварительной обработки данных. Выполнен анализ методов предварительной обработки и компрессии числовых данных. Выполнен анализ методов предварительной обработки и компрессии числовых данных. Произведен анализ результатов их применения в сенсорных сетях для понижения энергопотребления. Выбраны наиболее перспективные алгоритмы.
Ключевые слова: алгоритмы компрессии числовых данных,энергопотребление, сенсорные сети.
Постановка проблемы.
Сенсорная сеть, представляет собой совокупность взаимодействующих узлов, связанных с внешней средой датчиками (сенсорами). В каждом узле имеется вычислительное устройство (процессор) и приемопередатчик. После первичной обработки информация передается узлом по (беспроводной) коммуникационной сети в центральный пункт, где поступающая от всех узлов информация анализируется и обрабатывается в совокупности [1]. Одним из главных требований к таким сетям является автономность, выполнить которое можно уменьшив энергопотребление каждого узла. Для решения данной проблемы используют следующие методы:
- определение времени включения передачи;
- многозвенная передача, т.е. отправка сообщений через промежуточные узлы вместо прямой дальней передачи;
- предварительная обработка и сокращение объема данных, необходимых для передачи [2]. Одним из способов такой обработки может стать компрессия.
Также стоит отметить, что большинство мобильных устройств, выполняющих функции узлов сенсорной сети, не имеет сопроцессора для выполнения операций с вещественными числами.
Анализ литературы. Проведен анализ методов сжатия числовых данных. Основными подходами в этом направлении являются:
- словарное сжатие;
- статистическое кодирование;
- различные методы предварительной обработки данных[3].>
Для решения нашей задачи не применимы словарные методы, т.к. они потребляют довольно много ресурсов. Среди оставшихся необходимо выбрать алгоритмы, которые гарантируют быструю обработку в любых случаях и дают хоть какой то коэффициент сжатия. К таковым относятся методы упаковки бит, аппроксимации, а также методы предварительной обработки данных с помощью различных фильтров.
Цель работы —определить алгоритмы предварительной компрессии сенсорных данных, обеспечивающих максимальную экономию энергопотребления.
Постановка задачи исследования.Пусть дана исходная последовательность вида
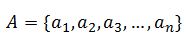 , , |
(1) |
где  —
некоторое число. Необходимо определить функционал F, преобразующий
исходную последовательность в последовательность байтов
—
некоторое число. Необходимо определить функционал F, преобразующий
исходную последовательность в последовательность байтов
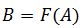 , а также функционал
, а также функционал
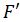 , выполняющий обратное преобразование
, выполняющий обратное преобразование
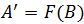 , где
, где
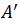 — также числовая последовательность вида
— также числовая последовательность вида
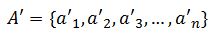 , , |
(2) |
причем максимальная погрешность такого преобразования не должна превышать некоторый заданный порог E:
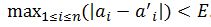 , , |
(3) |
На первом этапе необходимо определить такие методы, которые бы выполняли описанные выше условия, и в тоже время позволяли бы сократить энергопотребление узлов за счет уменьшения затрат на передачу данных. На втором этапе необходимо разработать автоматизированную систему, которая на основании предварительной информации о данных будет определять наилучшие параметры алгоритмов для их сжатия. В данной работе будет рассматриваться только первый этап.
Варианты решения. Для решения поставленной задачи были исследованы следующие методы:
-
упаковка бит. Основная идея заключается в том, что для кодирования
значений последовательности (1) можно использовать меньшее количество бит.
Новая битовая длина для каждого значения вычисляется по следующей формуле:
где max — максимальное значение в последовательности, min — минимальное значение в последовательности, dx — шаг изменения элементов;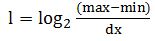 ,
,(4) -
целочисленное вейвлетное преобразование 5/3.
Был выбран конкретно этот вид вейвлетных преобразований,
так как он позволяет оперировать только целыми числами, а также хорошо
работает в большинстве случаев[4]. Исходная последовательность (1)
разделяется на две:
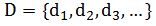 —
содержащую нечетные элементы;
—
содержащую нечетные элементы;  — содержащую четные. После этого формируются две новых последовательности
— содержащую четные. После этого формируются две новых последовательности
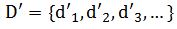 и
и 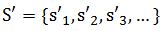 по следующим формулам:
по следующим формулам:
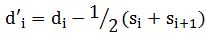 ,
,(5) 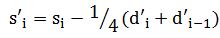 ,
,(6) На следующем шаге в качестве исходной последовательности принимается
 и алгоритм повторяется рекурсивно[4];
и алгоритм повторяется рекурсивно[4]; - алгоритм Рамера-Дугласа-Пеккера. Суть алгоритма заключается в том, чтобы уменьшить число точек кривой, аппроксимированной большой серией точек. Сжатие данных достигается за счет отбрасывания точек, которые могут быть восстановлены с заданной точностью E[5].
Структура входных данных.Одной из компаний, внедряющих сенсорные сети, является Modular Mining Systems. На рисунке 1 приведена структура данных и протоколов, которые применяются этой компании. Как можно заметить, данные представлены в двух измерениях: временной отсчет и идентификатор датчика, которому принадлежит данное значение. Поэтому входные последовательности(1) для алгоритмов компрессии можно генерировать двумя способами: отдельно по каждому датчику и по каждому временному отсчету.
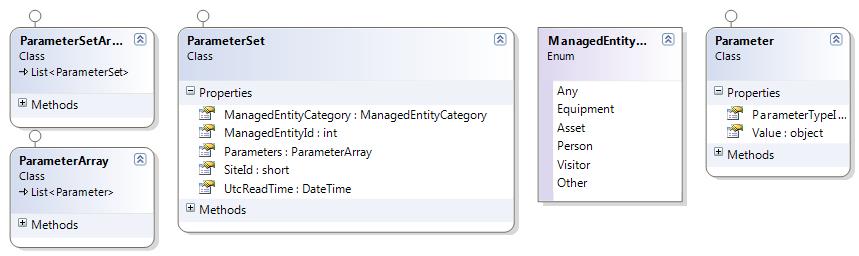 , , |
| Рисунок 1 — структура данных сенсорных сетей в Modular Mining Systems |
Экспериментальное исследование. Для проведения экспериментального сравнения работы алгоритмов был разработан генератор исходных данных, который создает структуру данных Modular Mining Systems, содержащую информацию от указанного количество датчиков. Данные измерений генерируются по нормальному закону распределения с указанными параметрами. Также реализована возможность внесения постоянного и импульсного шумов. Для выполнения непосредственно исследования было разработано приложение, позволяющее измерить время компрессии и декомпрессии, среднюю и максимальную ошибку алгоритма, коэффициент сжатия, а также визуально отобразить исходную и восстановленную последовательности. Интерфейс приложения можно увидеть на рисунке 2. Непосредственно для проведения тестов были сгенерированы данные со следующими параметрами: математическое ожидание — 50; стандартное отклонение — 10. Зашумление исходных данных почти не влияло на результаты работы и поэтому в данной статье не представлено. Параметры методов с потерями подбирались таким образом, чтобы максимальная ошибка не превышала 10%. Алгоритмы тестировались в ситуациях с различным количество измерений и различным количеством датчиков. Также была протестирована работа алгоритмов в случаях построения последовательностей по временным отсчетам и по отдельным датчикам. Непосредственно результаты работы алгоритмов представлены в таблицах 1-4.
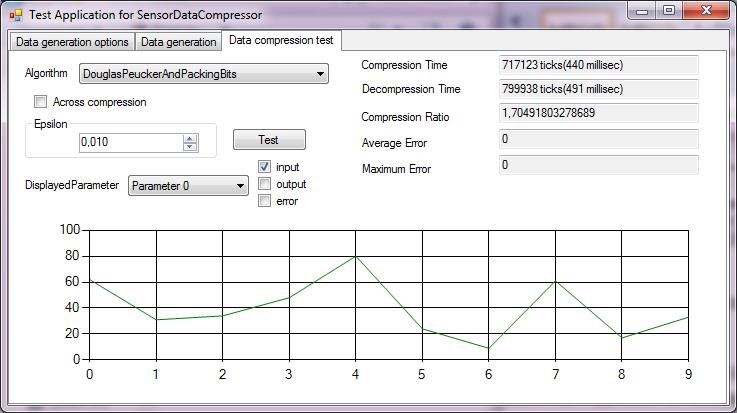 , , |
| Рисунок 2 — экранная форма приложения для тестирования алгоритмов |
| Таблица 1 — Результаты исследования для случая мало параметров(10), много измерений(10), построение последовательностей отдельно по каждому датчику |
 , , |
| Таблица 2 – Результаты исследования для случая мало параметров(10), много измерений(10), построение последовательностей по временным отсчетам |
 , , |
| Таблица 2 – Результаты исследования для случая мало параметров(10), много измерений(10), построение последовательностей по временным отсчетам |
 , , |
Как видно из таблиц 1 и 2 при достаточном количестве измерений алгоритмы работают лучше, если строить последовательности отдельно по каждому датчику. При дальнейшем увеличении количества измерений эта тенденция проявляется все ярче.
| Таблица 3 — Результаты исследования для случая много параметров(50), мало измерений(3), построение последовательностей отдельно по каждому датчику |
 , , |
| Таблица 4 — Результаты исследования для случая много параметров(50), мало измерений(3), построение последовательностей по временным отсчетам |
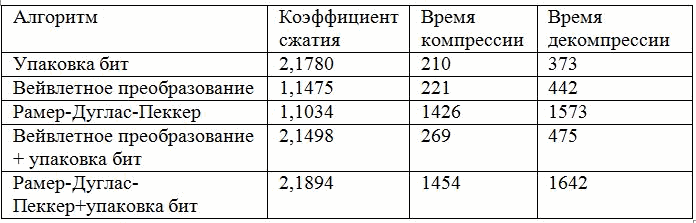 , , |
При уменьшении количества измерений становится более эффективно формировать последовательности для временных отсчетов. В целом можно отметить, что коэффициент сжатия алгоритмов находится в прямой зависимости от длины входящей последовательности. Но даже на таких небольших тестах мы видим, что алгоритмы эффективны и их применение не бесполезно. С точки зрения коэффициента сжатия конечно же выделяется последовательное применение алгоритма Рамера-Дугласа-Пеккера и упаковки бит. В тоже время вариант вейвлетного преобразования и упаковки бит хоть и проигрывает в отношении коэффициента сжатия, но зато выигрывает в скорости работы. Конечный выбор алгоритма должен главным образом зависеть от конкретных характеристик узлов сенсорной сети, а именно энергозатрат на работу процессора и передачу данных[6], так как в некоторых случаях дополнительное сжатие не покроет затраты на работу процессора мобильного устройства.
Выводы.Проведен анализ методов компрессии сенсорных данных для понижения энергопотребления сенсорных сетей. Экспериментальный анализ показал эффективность данного подхода. Выбраны два наиболее перспективных алгоритма. В дальнейшем можно провести оптимизацию выбранных алгоритмов. Получены исходные данные для разработки системы, которая по предварительному анализу данных будет выбирать алгоритм, который с высокой вероятностью покажет лучший результат в данном конкретном случае.
Список литературы:
-
А.С. Дмитриев, Л.В. Кузьмин, А.И. Панас
Применение теории динамического хаоса в современных проблемах сверхширокополосной радиосвязи
, 2011 г. -
П.В. Галкин, Д.В. Карловский
Особенности реализации беспроводных сенсорных сетей на основе технологии zigbee
, 2010 г. -
М.А. Смирнов,
Обзор применения методов безущербного сжатия данных в СУБД
, 2003 г. -
Michael D. Adams, Faouzi Kossentini
Reversible Integer-to- Integer Wavelet Transforms for Image Compression: Performance Evaluation and Analysis
, 1999 г. -
Википедия / Интернет-ресурс. — Режим доступа: http://ru.wikipedia.org/wiki/Алгоритм_Рамера_–_Дугласа_–_Пекера — Загл. с экрана.
-
Ranganathan Vidhyapriya, Ponnusamy Vanathi
Energy Efficient Data Compression in Wireless Sensor Networks
, 2008 г.