УДК 621.391.1
Сжатие числовых данных в системах обработки информации на ЭВМ
Авторы: Б.Я.Кавалерчик
Описание: Для кодирования числовых данных в системах обработки информации на ЭВМ (СОИ) предлагается использовать один из вариантов комбинаторно-нумерационного метода. Рассматриваются задачи кодирования для наиболее распространенных в СОИ форматов данных. Указывается на широкое практическое использование метода в автоматизированных системах управления.
Источник: http://www.mathnet.ru/
Введение
Большинство систем обработки информации на ЭВМ (СОИ), особенно при решении экономических задач, характеризуется низкой загрузкой (в лучшем случае 25—40%) центрального процессора (ЦП) при весьма высокой нагрузке на каналы ввода-вывода [1, 2 и др.]. Основной причиной непропорциональной загрузки ЦП и каналов обмена является, на наш взгляд, исторически сложившаяся со времен первых ЭВМ форма представления данных на магнитных носителях, ориентированная на быстрейшее выполнение команд в оперативной памяти. Естественно, что такое представление данных обладает значительной избыточностью. Имеющийся резерв времени ЦП можно использовать для программного ускорения обмена между оперативной памятью ЭВМ и внешними запоминающими устройствами, применяя сжатые формы представления данных на магнитных носителях.
Применение сжатых форм представления данных в СОИ дает ряд преимуществ. Во-первых, за счет перераспределения нагрузки между ЦП и каналами ввода-вывода значительно повышается производительность СОИ в целом. Во-вторых, уменьшаются объемы архивов магнитных носителей и повышается надежность хранения информации. И, в-третьих, уменьшаются объемы информации, передаваемой по линиям связи в режиме межмашинного обмена. Целесообразность использования сжатых форм представления данных в СОИ особенно ясна, если учесть основные тенденции развития вычислительной техники и средств связи: быстродействие ЦП возрастает, а стоимость выполнения одной команды падает на несколько порядков быстрее, чем растет скорость обмена; объемы файлов на магнитных дисках ежегодно почти удваиваются; тарифы на услуги связи снижаются в 10 раз медленнее, чем стоимость обработки информации на ЭВМ [3, 4].
В связи с этим вопросы разработки методов сжатия данных, ориентированных на использование в СОИ, являются весьма актуальными. Естественно, методы сжатия должны учитывать как специфику данных в СОИ, так и возможность экспериментальной оценки необходимых характеристик сжимаемой информации.
В настоящее время в СОИ используются различные методы сжатия информации.
В ряде систем управления базами данных [5] используются методы типа кодирования длин серий.
Достаточно часто используются методы, в которых последовательность независимых событий описывается последовательностью m-значных двоичных или десятичных чисел, а затем методы кодирования дискретного стационарного источника без памяти применяются для кодирования полученного цифрового потока, хотя его символы уже не являются независимыми. Несмотря на то, что при кодировании учитывается только различная вероятность появления различных цифр и игнорируется их статистическая зависимость, во многих конкретных случаях достигается заметное сжатие информации.
Обзор различных методов сжатия и некоторые примеры их использования в СОИ приведены в работах [6—11].
В настоящей работе на основании специфики данных в СОИ, экспериментальных результатов и требований к реализации процедур кодирования- декодирования производится выбор метода сжатия и структуры кода для наиболее распространенных форматов числовых данных.
Специфика данных в СОИ
В СОИ, особенно при решении экономических задач, числовые данные чаще всего представляются в двоичном или десятичном формате с фиксированной точкой. Обозначение формата F(n, m) соответствует n-значным числам, содержащим m знаков после точки. В оперативной памяти ЭВМ и на магнитных носителях данные с фиксированной точкой представляются в виде целых n-значных чисел, точка в числе явно не присутствует и при обработке информации задается программно.
Анализ данных в СОИ показывает, что количество значащих цифр во многих случаях значительно меньше предусмотренного форматом. Покажем это на конкретных примерах.
1. Данное «количество работающих на предприятии, в организации» может принимать значения до 100 000, т. е. должно иметь формат F(6, 0) в десятичном представлении. Однако предприятий-гигантов мало, в большинстве случаев численность работающих составляет десятки или сотни человек.
2. Данные количество товара на складе, в магазине
и цена товара
в рублях
могут принимать любые значения в формате F(9, 3). Однако
наиболее часто количество бывает целым от 1 до 100. Очень большие
и нецелые значения количества встречаются относительно редко. Цена
также редко бывает очень большой.
3. Данные часто имеют небольшое количество значащих цифр из-за округления при заданной относительной точности.
Таким образом, характерной особенностью числовых данных в СОИ во многих случаях является большое число ведущих и концевых нулей.
Высокая частота цифры 0 в данных СОИ отмечалась рядом авторов. Так, в [8] приводится пример типичного файла, в котором вероятность 0 в среднем в 16,3 раза выше вероятности появления любой другой цифры от 1 до 9. В работе [11] при исследовании эффективности метода универсального кодирования для условий бортовых информационных систем рассматривается двоичный поток с вероятностью 0 от 0,9 до 0,999.
Однако для выбора эффективного метода кодирования очень важно, что 0 не просто чаще других цифр встречается в представлении чисел,, а соответствует ведущим и концевым нулям.
Как уже отмечалось, при больших различиях в вероятностях появления 0 и других цифр методы кодирования дискретного стационарного источника без памяти обеспечивают некоторое сжатие информации. Учет специфики данных в СОИ (т. е. в конечном итоге статистической зависимости цифр в представлении чисел) позволяет, используя простые методы, достичь гораздо большей степени сжатия информации.
Метод кодирования. Выбор структуры составного комбинаторного кода
Если некоторое числовое данное может принимать N различных значений, то задача оптимального кодирования теоретически решается путем построения кодов переменной длины (например, кодов Хафмана [12]) для алфавита из N букв. Однако для больших N такое решение практически не реализуемо как из-за сложности кодирования, так и незнания статистики.
При выборе метода кодирования необходимо учитывать, что статистические характеристики данных должны определяться экспериментально путем просмотра файлов на магнитных носителях. С учетом специфики данных в СОИ наиболее естественно все множество значений разбивать на некоторые подмножества и определять вероятности попадания чисел в каждое из них. Для кодирования затем можно использовать следующий метод, являющийся одним из вариантов комбинаторно-нумерационного метода [13, 14].
Пусть множество М значений некоторого числового данного разбито на подмножества Mh М2,..., Мк, характеризующиеся числом возможных значений Nj и вероятностью попадания числа в данное подмножество qj, j=1,.., К. Пусть i=l,.., Nj — номер числа в подмножестве Мj. Тогда паре (j, i) ставится в соответствие два кодовых слова длины lj и log2 Nj, средняя длина результирующего кода равна
 , , |
Необходимым условием эффективности метода является существенное различие значений Nj/qj для разных подмножеств. Далее первое кодовое слово будем называть индексом.
В качестве примера рассмотрим применение данного метода для кодирования целых положительных десятичных чисел формата F(n, m) с относительной частотой целых значений р. Поскольку множество значений чисел разбито только на 2 подмножества (целые и дробные), индекс является однобитовым. Вместо номера числа в подмножестве дробных чисел для простоты целесообразно использовать значение числа, увеличенное в 10m раз. Средняя длина кода равна p(1+log210n-m) + (1-p) * (1+log210n). При p>1/log210m данное представление более эффективно, чем равномерный код. Отметим, что приведенный пример соответствует довольно распространенному в экономических системах случаю, когда целые значения встречаются значительно чаще дробных.
В СОИ при выборе рационального способа кодирования перед записью на магнитный носитель или передачей по линиям связи необходимо учитывать ряд факторов: избыточность кодирования; число операций, необходимых для кодирования-декодирования; объем требуемой оперативной памяти ЭВМ. Чтобы сжатое представление данных на магнитных носителях было выгодным, необходима достаточно высокая скорость процедур кодирования-декодирования, так как желательно выполнять всю процессорную обработку во время ожидания завершения операций ввода-вывода.
Скорость кодирования-декодирования определяется выбором первого когда и алгоритмом перехода от значения числа к его номеру в соответствующем подмножестве и обратно.
Рассмотрим две важнейшие задачи.
Задача 1. Кодирование целых неотрицательных двоичных чисел (формат F(n, 0)).
При использовании двоичных кодов постоянной длины (а это одно нехарактерных представлений в ЭВМ) требуется n бит информации на одно число.
В случае, если никакой дополнительной информации (кроме большого числа ведущих нулей) не имеется, наиболее естественным является разбиение на (n+1) подмножество по числу ведущих нулей.
Для простоты программной реализации можно рекомендовать следующий код:
индекс кодируется равномерным двоичным кодом;
вместо номера числа в подмножестве используется собственно число без ведущих нулей (в соответствии с значением индекса);
допускается объединение нескольких соседних подмножеств в одно.
При этом числа представляются в следующей форме: к бит занимает индекс j=0,.., 2k-1, а следующие n бит — собственно число. Считаем, что
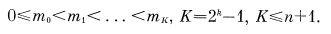
Рассмотрим задачу о выборке оптимального представления чисел. Допустим, что известны (определены экспериментально) частоты Р{ попадания значений числа в интервалы (0, 2i-1), i=0,..,n. Отметим, что в данном представлении получение дополнительной статистики не может уменьшить избыточность. Для удобства программной реализации и повышения быстродействия программ кодирования-декодирования во многих случаях можно рассматривать только интервалы (0,16i-1), т. е. брать возможные значения длины числа выравненными на границу полубайта.
Задачу выбора значений k, m0, m1..., mк для минимизации средней длины кода несложно решить методом динамического программирования [15].
Задача 2. Кодирование целых неотрицательных дробных десятичных чисел (формат F(n, m)).
В отличие от задачи 1 дробные числа в файлах СОИ часто характеризуются большим числом нулей как в начале, так и в конце данного. Наиболее просто и естественно разбиение на подмножества произвести по числу ведущих и концевых нулей.
Для задачи 2 также целесообразно использовать индекс постоянной длины, а вместо номера числа в подмножестве — собственно число с отбрасыванием соответствующего индексу количества ведущих и концевых нулей.
Аналогично задаче 1 также можно сформулировать и решить задачу минимизации средней длины кода.
Оценка эффективности метода
Для оценки эффективности методов сжатия данных рассмотрим несколько примеров на информации конкретных СОИ.
Пример 1. Некоторый файл, содержащий свыше 1 млн. записей,
включает данное наличие запасных частей на складе
, принимающее
 , , |
 , , |
 , , |
значения от 1 до 220-1. Числа Ni значений с фактической значностью i (т. е. с числом ведущих нулей 20-i) определены просмотром всех записей файла на ЭВМ и приведены в табл. 1.
Представление числа в обыкновенном двоичном фиксированном формате имеет длину 20 байт. Для распределения частот, приведенного в табл. 1, энтропия равна 5,98. Если бы измерения частот проводились только для i=i, 8, 12, 16, 20 (выравнивание на границу полубайта), энтропия равнялась бы 6,40.
Поскольку энтропия при выравнивании на границу полубайта увеличивается незначительно (на 7%), для кодирования можно ограничиться этими значениями.
В случае индексов постоянной длины оптимальным является представление с двумя битами на индекс (k=2) и длинами чисел m0=4, m1=8, m2=12, m3=20. Средняя длина кода при этом равна 7,41 бит.
Сравним предложенный метод кодирования с методом посимвольного кодирования цифрового потока. Для двоичных чисел в исходной форме частота появления цифры 0 составляет р=0,88. Для данного значения р энтропия равна 0,529, а средняя длина кода при использовании любых методов, использующих только разные вероятности появления 0 и 1 в представлении числа, не может быть сделана меньше 10,58. Таким образом, предлагаемый метод даже в простейшем варианте (с индексом постоянной длины) обеспечивает уменьшение средней длины кода в 10,58/7,41 = 1,43 раза по сравнению с нижней оценкой для метода посимвольного кодирования.
Пример 2. Некоторый файл содержит около 1,26 млн. записей, каждая
из которых включает данные количество
и цена
, имеющие формат
F(9,3) и занимающие 5 байт (40 бит). Просмотром файла на ЭВМ получено распределение фактической значности реквизитов, приведенное
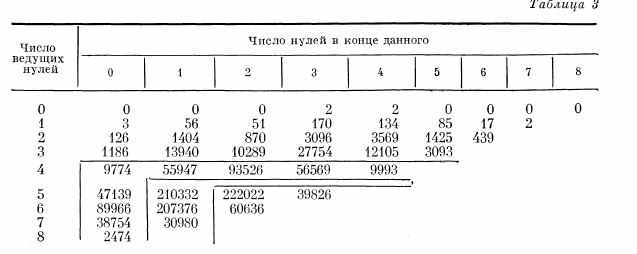
соответственно в табл. 2 и 3.
Для распределения, приведенного в табл. 2, энтропия равна 6,7. Применяя простейшее представление с индексом постоянной длины (2 бита) и разбиением на 4 подмножества (целые однозначные (формат F(1,0)), целые двузначные (F(2,0)), целые трехзначные (F(3,0)) и все остальные (F(9,3)), получаем среднюю длину кода 8,9 (разбиение показано на табл. 2). Аналогично для табл. 3 энтропия равна 11,6, а представление с форматами F(2,l), JF(3,2), F(5,3), F(9,3) дает среднюю длину кода 14,8.
Таким образом, даже применение простейшего сжатого представления обеспечивает уменьшение объемов информации в 2,7-4,5 раза.
Отметим, что в СОИ распределения, задаваемые таблицами типа 1—3, как правило, весьма незначительно изменяются со временем. Так, например, оценка информации ежедневно обновляемых файлов для табл. 1— 3, проведенная дважды с интервалом около года, дала практически одинаковые результаты.
Заключение
Предложенные методы положены в основу разработки математического обеспечения автоматизированной системы управления снабжением сельского хозяйства [16, 17], а также используются в ряде других АСУ. Опыт практического использования данных методов даже в простейших вариантах подтверждает, что при небольшом увеличении загрузки процессора достигается сжатие информации в 3-9 раз и время выполнения программ сокращается в 1,5-3 раза. Процедуры сжатия особенно эффективны при межмашинном обмене информацией.
В связи с высокой эффективностью использования методов сжатия информации в СОИ можно высказать следующие предложения: ввести в состав систем управления базами данных и операционных систем ЭВМ модули для работы со сжатыми формами представления данных; предусмотреть, особенно во вновь проектируемых ЭВМ, аппаратные средства для работы со сжатыми данными.
С учетом большого и постоянно возрастающего числа эксплуатируемых СОИ реализация данных предложений может дать весьма существенный экономический эффект.
В заключение автор выражает свою искреннюю благодарность и признательность Ю. М. Штарькову за весьма полезное обсуждение и ряд ценных советов.
Литература
-
Андон Ф. И., Дерецкий В. А., Поляченко Б. Е. Интегрированное мультипрограммирование в ОС ЕС//Управляющие системы и машины. 1982. № 5. С. 58—62.
-
Назаров С. В., Барсуков А. Г. Генерация операционной системы ОС ЕС. М.: Финансы и статистика, 1985.
-
Пржиялковский В. В., Ломов Ю. С. Технические и программные средства Единой системы ЭВМ (ЕС ЭВМ-2). М.: Статистика, 1980.
-
Громов Г. Р. Современная индустрия обработки данных //Изв. АН СССР. Техн. кибернетика. 1982. № 5. С. 173—198.
-
Системы управления базами данных для ЕС ЭВМ. Справочник. М.: Финансы и статистика, 1984.
-
Бабкин В. Ф., Крюков А. Б., Штарьков Ю. М. Сжатие данных//Аппаратура для космических исследований. М.: Наука, 1972. С. 172—209.
-
Акушский И. Я., Фусман В. М., Хабаров В. С. Сжатие информационных массивов (на примере текстовой информации) //Пробл. МСНТИ. 1980. № 3. С. 54—63.
-
Мартин Дж. Организация баз данных в вычислительных системах. М.: Мир, 1980.
-
Цымбал В. П., Куценко С. П. Информационные системы и структуры данных. Киев: Вища школа, 1980.
-
Гайский В. А., Гусев В. П. Кодовая дельта-модуляция//Автометрия. 1974. № 5. С. 49—58.
-
Кларин А. П., Шурыгин В. А. Исследование эффективности универсального кодирования в зависимости от длины блока // Пробл. передачи информ. 1984. Т. 20. № 2. С. 105—110
-
Хаффман Д. А. Метод построения кодов с минимальной избыточностью//Кибернетический сб. М.: Изд-во иностр. лит., 1961. Вып. 3. С. 79—87.
-
Shtarkov Yu. M., Babkin V. F. Combinatorial encoding for discrete stationary sources // Proc. 2nd Internat, Symp. Inform. Theory, Tsahkadsor, Armenia, USSR, 1971. Budapest: Acad. Kiado, 1973. P. 249—256.
-
Штарьков Ю. М. Обобщенные коды Шеннона // Пробл. передачи информ. 1984. Т. 20. № 3. С. 3—16.
-
Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. М.: Наука, 1965.
-
Игольников Л. Ш., Кавалерчик Б. Я., Паук В. Г. Автоматизированная система управления материально-техническим снабжением сельского хозяйства Белорусской ССР//Управляющие системы и машины. 1980. № 2. С. 120—123.
-
Кавалерчик Б. Я., Гришкан В. И. Автоматизированная система планирования потребности в запасных частях // Управляющие системы и машины. 1983. № 4. С. 114—117.