Реферат за темою випускної роботи
Зміст
- Введення
- 1. Актуальність теми
- 2. Мета і завдання дослідження, плановані результати
- 3. Наукова новизна в області застосування
- 4. Загальна постановка проблеми
- 4.1 Основні фактори, що впливають на вибір страхового пакету
- 4.2 Пошук рішень в ієрархії просторів
- 4.3 Пошук рішень в альтернативних просторах
- 4.4 Пошук рішень з використанням декількох моделей
- 4.5 Нейлоровскіе діагностуючі системи
- 4.6 Вибір методу розв'язання задач
- Висновки
- Список джерел
Введення
Сучасні страхові компанії надають широкий спектр послуг зі страхування транспортних засобів, і клієнтам не завжди буває легко розібратися у всіх існуючих пропозиціях і підібрати найбільш відповідний їм вид страхування.
Дана робота являє собою опис з розробки прототипу експертної системи, метою якої є допомога у визначенні оптимального варіанту страхування. Дана система покликана замінити експерта-консультанта в обраній предметній області.
1. Актуальність теми
У зв'язку із зростанням технічних можливостей сучасних обчислювальних систем з'являється все більше і більше можливостей по обробці даних. Технічний прогрес не обійшов стороною страхові компанії. У багатьох зарубіжних компаніях використовується велика кількість складних скорингових систем. Актуальність обумовлена ??зростанням потреби Українських страхових компаній в ефективному андеррайтингу у зв'язку з розвитком страхового ринку і фактично повною відсутністю впроваджених скорингових систем.
2. Мета і завдання дослідження, плановані результати
Мета: Розробка комп'ютеризованої скорингової системи підтримки прийняття рішень страхування автомобілів.
Основні завдання дослідження:
- Дослідження процесів андеррайтингу
- Вивчення факторів, що впливають на вибір страхового портфеля
- Знаходження оптимального страхового портфеля
- Дослідження методів прогнозування страхових випадків
- Вибір оптимального методу для створення ЕС
3. Наукова новизна в області застосування
Скорингової система підтримки прийняття рішень страхування автомобілів створює широкий спектр можливостей по зручному підбору страхового пакету без безпосереднього контакту з представником страхової компанії. На сьогоднішній день існує велика різноманітність алгоритмів підбору страхового пакету, дають оптимальні результати. Однак, в Україні, не існує одного впровадженого універсального алгоритму, відповідного для будь-якого класу даних, а також виявляє ймовірність шахрайства при страхуванні. Крім того, різні алгоритми ведуть себе по-різному при обробці досить великих обсягів даних. У зв'язку з цим доцільно розробити алгоритм, який міг би одночасно підбирати страхові пакети для клієнтів, а також виявляти ймовірність шахрайства з боку клієнта.
4. Загальна постановка проблеми
4.1 Основні фактори, що впливають на вибір страхового пакету
4.2 Пошук рішень в ієрархії просторів
Методи пошуку рішень в одному просторі зазвичай діляться на:
Розглянемо пошук методом редукції
При пошуку методом редукції вирішення завдання зводиться до вирішення сукупності утворюють її підзадач. Цей процес повторюється для кожної підзадачі до тих пір, поки кожна з отриманого набору підзадач, що утворюють рішення вихідної задачі, не матиме очевидне рішення. Процес рішення задачі розбиттям її на підзадачі можна представити у вигляді спеціального спрямованого графа G, званого І / АБО-графом; Кожній вершині цього графа ставиться у відповідність опис деякої задачі (підзадачі). У графі виділяють два типи вершин: кон'юнктивні вершини і диз'юнктивні вершини.
Рішення завдання при пошуку методом редукції (при пошуку в І / АБО-графі) зводиться до знаходження в І / АБО-графі вирішального графа.
Мета процесу пошуку в І / АБО-графі - показати, що початкова вершина розв'язна, тобто для цієї вершини існує вирішальний граф [ 2 ].
4.3 Пошук рішень в альтернативних просторах
Розглянуті вище методи пошуку виходять з мовчазною передумови, що знання про предметну область і дані про розв'язуваної задачі є точними і повними і для них справедливо наступне:
Однак при вирішенні будь-яких практичних завдань і особливо при розв'язанні неформалізованих завдань поширена зворотна ситуація. Експертові доводиться працювати в умовах неповноти і неточності знань (даних) і, як правило, в умовах дефіциту часу. Коли експерт вирішує задачу, він використовує методи, які відрізняються від формальних математичних міркувань. У цьому випадку експерт робить правдоподібні припущення, які він не може довести; тим самим питання про їх істинності залишається відкритим. Усі твердження, отримані на основі цих правдоподібних припущень, також не можуть бути доведені [ 2 ].
4.4 Пошук рішень з використанням декількох моделей
Всі методи пошуку, розглянуті досі, використовували при поданні проблемної області якусь одну модель, тобто розглядали область з якоїсь однієї точки зору. При вирішенні складних завдань в умовах обмежених ресурсів використання декількох моделей може значно підвищити потужність системи. Об'єднання в одній системі декількох моделей дає можливість подолати такі труднощі:
Слід зазначити, що використання декількох моделей вимагає додаткових знань про те, як створювати і об'єднувати різні точки зору.
4.5 Нейлоровскіе діагностуючі системи
Розроблена К. Нейлор концепція побудови ЕС заснована на загальній байесовской схемою. Основні принципи, реалізовані в даній ЕС, включають:
Перше ускладнення, яке вводиться в загальну схему байєсівського підходу, пов'язане з використанням верхніх і нижніх порогів для ймовірностей окремих гіпотез. Якщо ймовірність Р (Н) після врахування всіх свідоцтв перевершує верхній поріг М1 (Н):
Р (Н)> М1 (Н),
то гіпотеза Н приймається як основа для можливого ув'язнення. Якщо ж
Р (Н) <М2 (Н),
де М2 (Н) - нижній поріг, то гіпотеза Н відкидається як неправдоподібна.
Є підстави встановлювати верхні і нижні пороги M1, М2 індивідуально для кожної гіпотези відповідно до наявної в СППР базою знань і максимальних можливих рівнів ймовірностей гіпотез з урахуванням всіх принципово можливих свідчень. Наприклад, можна вважати
М1 (Н) = 0,9 Рмах (Н), М2 (Н) = 0,5 М1 (Н),
де Рмах (Н) - максимальна можлива ймовірність, досяжна для даної гіпотези, за умови, що всі свідчення, наявні в базі знань і пов'язані з цією гіпотезою, будуть підтверджені користувачем на користь гіпотези Н.
Величини Рмах (Н) для всіх Н, так само як і М1 (Н), М2 (Н), очевидно, можуть бути обчислені заздалегідь і також включені в базу знань СППР.
Облік невизначеності, укладеної у відповідях користувача на питання СППР, є важливим моментом в організації діалогу. В ідеалі ми могли б припустити, що на питання СППР користувач відповідає або "так", або "ні" (є висока температура у пацієнта, немає високої температури і т. д.), тобто виконується дане свідоцтво Е або не виконується .
Більш реалістичною є ситуація, коли користувач з якоїсь причини або хоче ухилитися від відповіді (якщо, наприклад, питання занадто складний і не відповідає кваліфікації користувача в даній предметній області), або прагне дати не надто певний відповідь. Наприклад, якщо задається питання про наявність підвищеної температури у пацієнта, то необхідно дати користувачеві можливість проранжувати ступінь підвищення температури, наприклад, відповідно до 11-бальної шкалою:
Присутні й всі проміжні цілі значення шкали від -5 до +5.
У результаті кожне свідчення Е буде оцінюватися за цією шкалою на підставі відповіді користувача
Відповідно до байєсівського підходом після обробки чергового свідоцтва Е ми обчислювали ймовірність Р (Н / Е) і замінювали нею попередню ймовірність Р (Н). Тепер ми повинні запропонувати спосіб обчислення не Р (Н / Е), а Р (Н / R). Це може бути виконано наступним чином. По-перше, випадок R = 5 повинен відповідати ймовірності Р (Н / Е), обчисленої за формулою Байєса. По-друге, варіант R = -5 повинен відповідати величині Р (Н / Е). Остання ймовірність може бути знайдена з співвідношень:
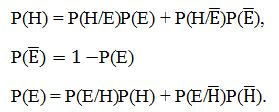
По-третє, випадок R = О (НЕ ЗНАЮ), очевидно, не повинен змінювати апріорну ймовірність Р (Н) і тому тут маємо:
Ми отримали три характерні точки на графіку Р (Н / R) як функції R, Проміжні значення Р (Н / R) пропонується відновлювати за допомогою лінійної інтерполяції. Таким чином, для будь-якого НЕ R приналежному R ми отримуємо відповідне значення Р (Н / R), що і було потрібно. При цьому максимальне значення Р (Н / R) дорівнюватиме Р (Н / Е) і відповідати випадку R = 5, як і вказувалося раніше [ 3 ].
4.6 Вибір методу розв'язання задач
Оскільки основним завданням розробки даної СППР є підбір оптимального пакету страхування, то вважаю логічним використовувати нейлоровскіе діагностуючі системи, тому що завдяки такій структурі ми можемо з певними ймовірностями визначити придатність страхового пакету для кожного автовласника.
Використовуємо метод Нейлора до нашої області і складемо зразок БЗ для СППР страхування автомобілів.
Гіпотези Hi:
Страховий пакет 1; 0,1; 5; (1, 0, 0.99), (2; 0,7; 0,05); (4; 0,2; 0,5); (5, 0, 0,99 ); (6; 1; 0,01);
Страховий пакет 2; 0,05; 2, (2; 1; 0,01); (6; 0,9; 0,02);
Страховий пакет 3; 0,01; 3; (3; 0,9; 0,1); (4; 0,25; 0,5); (6; 0,9; 0,02);
Страховий пакет 4; 0,01; 2; (4; 0,01; 0,5); (6; 0,9; 0,02).
Дамо розшифровку наведених записів. Апріорна ймовірність того, що власникові авто підійде страховий пакет 1, дорівнює 0,1. У даній базі знань зі страховим пакетом 2 пов'язані два (2) критерію.
Перший критерій - висока страхова сума. Ймовірність високої страхової суми тут покладена рівною 1. Ймовірність того, що при високій страховій сумі цей пакет не підійде дорівнює 0,01.
Другий критерій - марка моделі. Ймовірність дорогої марки авто при виборі страхового пакету 1 дорівнює 0,9. Ймовірність того, що при дорогий марці авто цей пакет не підійде дорівнює 0,02.
Свідоцтва Ei:
- Кількість страхових випадків; Багато страхових випадків?
- Розмір страхової суми; Велика страхова сума?
- Марка автомобіля - частота викрадень; Частота викрадень?
- Рік випуску авто; Новий автомобіль?
- Країна виробник авто; Країна виробника авто?
- Марка автомобіля - частота ДТП; Дорогая марка автомобіля?
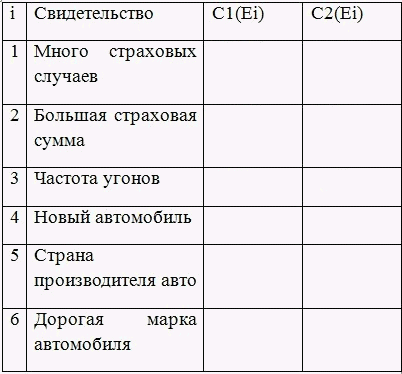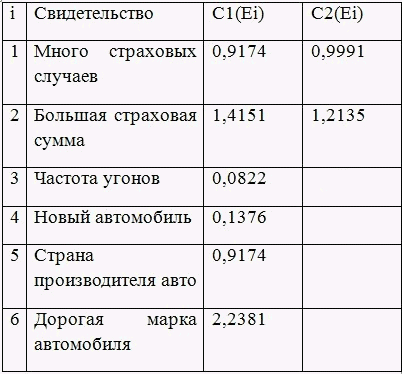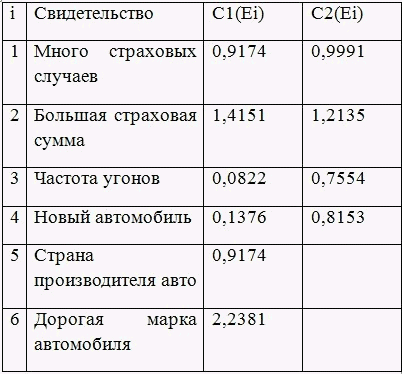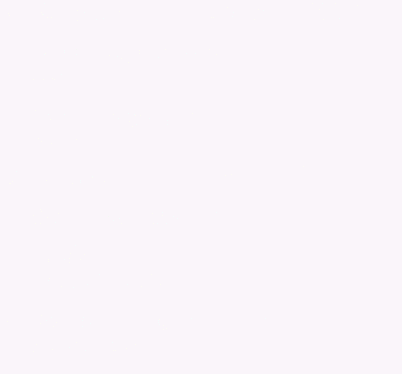
Згідно обчисленим вихідним цінами свідоцтв C1 (Ei) першим буде завжди задаватися питання, пов'язане зі свідоцтвом Е6 (у нього максимальна ціна 2,2381):
Дорога марка автомобіля?
При відповіді користувача ТАК (R = 5) ми можемо перерахувати масив P (Hi) і обчислити нові ціни свідоцтв C2 (Ei). З урахуванням нових цін свідоцтв буде заданий наступний питання, пов'язане зі свідоцтвом Е2 (у нього максимальна ціна 1,2135).
При цьому повідомлення про те, що марка автомобіля дорога, призвело до істотного збільшення цін і інших свідчень, що виглядає вельми природно.
Висновки
Проаналізовано методи створення СППР страхування автомобілів. Вибраний оптимальний метод. На підставі вибору привели приклад пошуку рішення. Надалі планується дослідження, яке дозволить визначити реальну «вагу» всіх факторів, а також вибрати середовище розробки даної СППР.
Важливе зауваження
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список джерел
- Попов Е.В. Експертні системи / Е.В.Попов. М.: Наука, 1987, с. 180 - 184.
- Нейлор К. Як побудувати свою експертну систему / К.Нейлор; пров. з англ. під ред. М.М. Слеповой. М.: Вища школа, 1991, с. 15 - 22.
- Черноруцкий І. Г. Методи прийняття рішень / Черноруцкий І. Г.: БХВ-Петербург, 2005, с. 65 - 70.
- Інформаційний сайт, присвячений темі страхування [Електронний ресурс]. - Режим доступу: http://www.insur-info.ru/
- Інформаційний сайт, рейтингового агентства [Електронний ресурс]. - Режим доступу: http://www.raexpert.ru/
- Офіційний сайт конгресу з андеррайтингу [Електронний ресурс]. - Режим доступу: http://underwriting-congress.ru/
- Архипов А.П. Андеррайтинг в страхуванні. Теоретичний курс і практикум: навчальний посібник для студентів вузів, що навчаються за спеціальністю 08.01.05. - М.: ЮНИТИ-ДАНА, 2007р., Стор 292
- Інформаційний сайт, присвячений темі страхування [Електронний ресурс]. - Режим доступу: http://insbizz.blogspot.com/
- Архипов А.П. Андеррайтинг в страхуванні. Теоретичний курс і практикум: навчальний посібник для студентів вузів, що навчаються за спеціальністю 08.01.05. - М.: ЮНИТИ-ДАНА, 2007р., Стор 107
- Інформаційний сайт, рейтингового агентства [Електронний ресурс]. - Режим доступу: http://www.raexpert.ru/
