РЕЗЮМЕ
Эта статья описывает алгоритм для автоматического обнаружения круглых форм в усложненных и шумных изображениях без использования условных преобразований Хафа. Предложенный алгоритм основан на недавно разработанной технике роевого интеллекта, известной как оптимизация передвижением бактерий (BFO). Новая целевая функция была получена, чтобы сравнить подобие круга кандидата с фактическим кругом на граничной карте входного изображения, основанного на различии их местоположений центра и длин радиусов. Руководствуясь значениями этой целевой функции (чем меньше, тем лучше) ряд закодированных кругов кандидатов развивается, используя алгоритм BFO, таким образом, чтобы они могли соответствовать фактическим кругам на граничной карте изображения. Предложенный метод в состоянии обнаружить один или мномножество окружностей на цифровом изображении за один шаг оптимизации. Результаты моделирования на нескольких синтетических и естественных изображениях, с переменным диапазоном сложности, подтверждают эффективность предложенной техники с точки зрения ее точности, скорости и надежности.
КЛЮЧЕВЫЕ СЛОВА
Распознавание объектов, роевой интеллект, бактериальное перемещение, машинное зрение
I. ВВЕДЕНИЕ
Прошлые несколько десятилетий наблюдался массивный рост в области основаных на биологических процессах алгоритмах для поиска и оптимизации. Вычислительная стоимость резко уменьшилась, исследователи со всех углов мира проявляют все больший интерес, следуя основным принципам природы, чтобы решить сложные проблемы оптимизации. Следуя этой традиции, практикующие специалисты в сфере машинного зрения также применяют такие алгоритмы к тяжелым задачам, которые появляются в этой сфере. Например, Wachowiak и др.(2004) применял метод роя частиц PSO, который основан на интеллектуальном поведении группы социальных существ в проблеме биомедицинской регистрации изображения. Дэ-Сиань и Цзянь-Чан (2008) применял ACO для того, чтобы улучшить границы цифровых изображений.
Автоматическое выявление и извлечение геометрических фигур из изображений очень полезно в ряде задач, потому что такие фигуры часто присутствуют в сделанном человеком окружении. Они также широко используются в качестве частей символов, используемых человеком. В частности проблемы обнаружения круга и эллипса были широко изучены в сообществе распознавания форм при помощи детерминированных методов, как преобразования Хафа (HT), которые часто требуют больших вычислений. Чтобы преодолеть эти ограничения, исследователи предложили новые подходы к HT, например, вероятностный HT, рандомизированный HT и нечеткий HT. Лэм и Юэн (1996) придумали гибридный подход, основанный на фильтровании гипотезы и HT, чтобы обнаружить круги. Новые целочисленные преобразования были также предложены в этом контексте (Беккер и др. (2002)). Как альтернатива основанным на HT методам, задача распознавания формы в компьютерном виденье решалась методами стохастического поиска, которые включают метод оценки параметров модели на основе случайных выборок (Fischer и Bolles 1981), алгоритм имитации отжига (SA) (Bongiovanni и Crescenzi 1995), и генетический алгоритм (GA) (Goldberg 1989). Стохастические алгоритмы подобно GA могут найти близкие к оптимальным решения очень быстро из-за обладания большим количеством неявного параллелизма. Однако, они не могут гарантировать достигнуть оптимального решения. Недавно был растущий интерес исследователей в использовании GA для важных задач обнаружения формы, например, Рот и Левин (1994) предложили использование GA для примитивного извлечения изображений. Латтон и др. выполнил дальнейшее совершенствование вышеупомянутого метода недавно в 2000 (Латтон и Мартинес 1994). Яо и др. (2004) придумал мультипопуляцию GA, чтобы обнаружить эллипсы. Айала Рамирес и др. (2006) представил основанный на GA датчик круга. Их подход способен к обнаружению множества кругов на реальных изображениях, но часто не обнаруживает маленькие и несовершенные круги.
Пэссино, (2002) предложил мощный алгоритм для реальной оптимизации параметра, теперь известной как оптимизация движением бактерий (BFOA) (Лю и Пэссино 2002). BFOA имитирует отдельное и сгруппированное поведение Escherichia coli, бактерии, живущей в нашем кишечнике. Алгоритм нашел успешное применение в нескольких проблемах реального мира как оптимальная конструкция контроллера (Лю и Пэссино 2002), гармоническая оценка (Mishra 2005), сокращение потерь при передаче (Tripathy и др. 2006), и мощность фильтра задержки. Эта работа описывает обнаружение кругов на цифровых изображениях, используя адаптивный вариант классического BFOA. Работа – не расширение методов HT, описанных раньше, и подает в целом новый подход для рассмотрения этой классической задачи компьютерного виденья. Мы используем детектор границ Кэнни (Кэнни 1986), для создания границ карты черно-белого изображения. Затем применяется адаптивный BFOA, чтобы искать по всей граничной карте круглую форму. Каждая бактерия здесь моделирует испытательный круг, и целевая функция будет получена из области таких испытательных кругов, чтобы измерить, до какой степени испытательный круг соответствует фактическому кругу на граничной карте изображения. Чем лучше тестовый круг приближается к фактическому граничному кругу, тем меньшим становится значение этой функции. Минимизация целевой функции с BFOA в конечном счете ведет к быстрому и устойчивому нахождению круглых форм на данном изображении. Сравнивая с одним современным основанным на GA методом и рандомизированным преобразованием Хафа (RHT) алгоритм на повторных изображениях указывает превосходство предложенного метода. Остальная часть статьи организована следующим образом.
II. КЛАССИЧЕСКИЙ BFOA: ОБЗОР
Предположим, что мы хотим найти минимум  , где
, где  (т.е.
(т.е. p-мерный вектор вещественных чисел) и у нас нет размеров или аналитического описания градиента
p-мерный вектор вещественных чисел) и у нас нет размеров или аналитического описания градиента 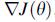 . BFOA подражает четырем основным механизмам, наблюдаемым в реальной бактериальной системе: хемотаксис, роение, репродукция и ликвидация рассеивания, чтобы решить проблему оптимизации неградиента. Ниже мы представляем формальные нотации, используемые в литературе BFOA, и затем обеспечиваем полный псевдокод алгоритма BFO.
. BFOA подражает четырем основным механизмам, наблюдаемым в реальной бактериальной системе: хемотаксис, роение, репродукция и ликвидация рассеивания, чтобы решить проблему оптимизации неградиента. Ниже мы представляем формальные нотации, используемые в литературе BFOA, и затем обеспечиваем полный псевдокод алгоритма BFO.
Давайте определим шаг хемотаксиса, который будет падением, сопровождаемым падением или падением, сопровождаемым выполнением. Пусть j это индекс для шага хемотаксиса. Пусть k это индекс для шага воспроизведения. Пусть l это индекс события ликвидации рассеивания. Кроме того, пусть
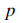 – измерение пространства поиска,
– измерение пространства поиска,
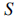 – общее количество бактерий в популяции,
– общее количество бактерий в популяции,
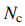 – количество шагов хемотаксиса,
– количество шагов хемотаксиса,
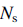 – длина бассейна,
– длина бассейна,
 – количество шагов репродукции,
– количество шагов репродукции,
 – число событий ликвидации рассеивания,
– число событий ликвидации рассеивания,
 – вероятность ликвидации рассеивания,
– вероятность ликвидации рассеивания,
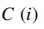 – размер шага в случайном направлении, указывающий на падение.
– размер шага в случайном направлении, указывающий на падение.
Пусть  представляет позицию каждого элемента в популяции бактерий на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. Пусть
представляет позицию каждого элемента в популяции бактерий на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. Пусть 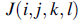 обозначают стоимость расположения i-й бактерии
обозначают стоимость расположения i-й бактерии  (иногда, мы отбрасываем индексы и обращаемся к i-й позиции бактерии как
(иногда, мы отбрасываем индексы и обращаемся к i-й позиции бактерии как  ). Обратите внимание на то, что мы будем взаимозаменяемо именовать J, как 'стоимость' (используя терминологию из теории оптимизации) и как питательную поверхностью (в отношении биологических соединений). Для фактической бактериальной популяции S может быть очень большим (напр. S=109), но p=3. В нашем компьютерном моделировании мы будем использовать намного меньшие численности популяции и сохраним численность популяции фиксированной. BFOA, однако, позволяет брать p>3 так, чтобы мы могли применить метод к задачам оптимизации больших размеров. Ниже, мы кратко описываем четыре главных шага в BFOA.
). Обратите внимание на то, что мы будем взаимозаменяемо именовать J, как 'стоимость' (используя терминологию из теории оптимизации) и как питательную поверхностью (в отношении биологических соединений). Для фактической бактериальной популяции S может быть очень большим (напр. S=109), но p=3. В нашем компьютерном моделировании мы будем использовать намного меньшие численности популяции и сохраним численность популяции фиксированной. BFOA, однако, позволяет брать p>3 так, чтобы мы могли применить метод к задачам оптимизации больших размеров. Ниже, мы кратко описываем четыре главных шага в BFOA.
- Хемотаксис. Этот процесс моделирует перемещения E. coli, плавание и падение через жгутики. Предположим
 представляет i-ю бактерию на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. C(i) – скаляр, размер шага в случайном направлении, указывающего на падение (выполнение модуля длины). Тогда в вычислительном хемотаксисе движение бактерий могут быть представлены, как
представляет i-ю бактерию на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. C(i) – скаляр, размер шага в случайном направлении, указывающего на падение (выполнение модуля длины). Тогда в вычислительном хемотаксисе движение бактерий могут быть представлены, как

Рисунок 2.1 – Формула движения бактерий в вычислительном хемотаксисе
где  указывает на вектор единичной длины в случайном направлении.
указывает на вектор единичной длины в случайном направлении.
- Роение. Интересное поведение группы наблюдалось для нескольких подвижных видов бактерий включая E. coli и S. typhimurium, где устойчивые пространственно-временные образцы сформированы в полутвердой питательной среде. Группа ячеек E. coli располагает себя в кольце перемещения, продвигаясь вверх по питательному градиенту, чтоб оказаться среди полутвердой матрицы с единственным питательным химио-эффекторным веществом. Когда ячейки стимулированы высоким уровнем сукцината, они выпускают аспартат аттрактанта, который помогает им агрегироваться в группы и таким образом перемещаться как концентрические образцы роев с высокой бактериальной плотностью. Межклеточная сигнализация в рое E. coli может быть представлена следующей функцией:
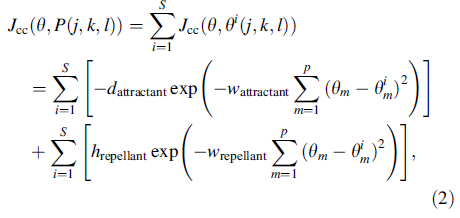
Рисунок 2.2 – Функция межклеточной сигнализации
где 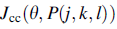 это значение целевой функции, которое будет добавлено к фактической целевой функции (для минимизации), чтобы представить время изменения целевой функции. Коэффициенты
это значение целевой функции, которое будет добавлено к фактической целевой функции (для минимизации), чтобы представить время изменения целевой функции. Коэффициенты 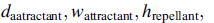 и
и  контролируют силу межклеточной сигнализации. Более конкретно
контролируют силу межклеточной сигнализации. Более конкретно  это глубина аттрактанта, выпущенного ячейкой,
это глубина аттрактанта, выпущенного ячейкой, 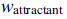 это мера ширины сигнала аттрактанта (квантификация уровня диффузии химиката),
это мера ширины сигнала аттрактанта (квантификация уровня диффузии химиката), 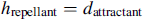 это высота эффекта репеллента (ячейка бактерии также отражает соседнюю ячейку в том смысле, что физически невозможно иметь две ячейки в одном и том же расположении), и
это высота эффекта репеллента (ячейка бактерии также отражает соседнюю ячейку в том смысле, что физически невозможно иметь две ячейки в одном и том же расположении), и  это мера ширины репеллента.
это мера ширины репеллента.
- Репродукция. Наименее здоровые бактерии в конечном счете умирают, в то время как каждая из более здоровых бактерий (те, которые приводят к меньшему значению целевой функции) разделяется на две бактерии, которые затем помещаются в том же месте. Это сохраняет размер роя постоянным.
- Ликвидация и рассеивание. Чтобы моделировать это явление в BFOA, некоторые бактерии ликвидируются наугад с очень маленькой вероятностью, в то время как новые в произвольном порядке инициализируются по пространству поиска.
Список использованной литературы
Abraham A, Guo H, Liu H (2006) Swarm intelligence: foundations, perspectives and applications, swarm intelligent systems. In: Nedjah N, Mourelle L (eds) Studies in computational intelligence. Springer, Germany, pp 3–25
Anwal RP (1998) Generalized functions: theory and technique, 2nd
edn. Birkhauser, Boston
Becker J, Grousson S, Coltuc D (2002) From Hough transforms to integral transforms. In: Proceedings of international geosciences and remote sensing symposium, IGARSS_02 3:1444–1446
Bongiovanni G, Crescenzi P (1995) Parallel simulated annealing for shape detection. Comput Vision Image Understanding 61(1):60–69 Canny J (1986) A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell 8:679–714
Das S, Biswas A, Dasgupta S, Abraham A (2009a) Bacterial foraging optimization algorithm: theoretical foundations, analysis, and applications, foundations of computational intelligence. Global optimization, studies in computational intelligence, vol 3. Springer, Germany, pp 23–55. ISBN: 978-3-642-01084-2
Dasgupta S, Das S, Abraham A, Biswas A (2009) Adaptive computational chemotaxis in bacterial foraging optimization: an analysis. IEEE Trans Evol Comput 13(4):919–941
Garcia S, Molina D, Lozano M, Herrera F (2008) A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: a case study on the CEC’2005 Special session on real parameter optimization. J Heurist. doi:10.1007/s10732-008-9080-4
Le Hegarat-Mascle S, Hegarat-Mascle L, Kallel A, Descombes X (2007) Ant colony optimization for image regularization based on a nonstationary markov modeling. IEEE Trans Image Process 16(3):865–878
Liu Y, Passino KM (2002) Biomimicry of social foraging bacteria for distributed optimization: models, principles, and emergent behaviors. J Optim Theory Appl 115(3):603–628
Lutton E, Martinez P (1994) A genetic algorithm for the detection 2-D geometric primitives on images. In: Proceedings of the 12th international conference on pattern recognition (ICPR_94), vol 1, Jerusalem, Israel, pp 526–528
Passino KM (2002) Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Systems Magazine, pp 52–67
Santamaria J, Cordon O, Damas S, Garcia-Torres JM, Quirin A (2009) Performance evaluation of memetic approaches in 3D reconstruction of forensic objects. Soft Comput 13(8–9):883–904
Wachowiak MP, Smolikova R, Yufeng Z, Zurada JM, Elmaghraby AS (2004) An approach to multimodal biomedical image registration utilizing particle swarm optimization. IEEE Trans Evol Comput 8(3):289–301
Yao J, Kharma N, Grogono P (2004) Fast robust GA-based ellipse detection. In: Proceedings of 17th international conference on pattern recognition ICPR-04, vol 2, Cambridge, UK, pp 859–862
 , где
, где  (т.е.
(т.е. p-мерный вектор вещественных чисел) и у нас нет размеров или аналитического описания градиента
p-мерный вектор вещественных чисел) и у нас нет размеров или аналитического описания градиента 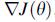 . BFOA подражает четырем основным механизмам, наблюдаемым в реальной бактериальной системе: хемотаксис, роение, репродукция и ликвидация рассеивания, чтобы решить проблему оптимизации неградиента. Ниже мы представляем формальные нотации, используемые в литературе BFOA, и затем обеспечиваем полный псевдокод алгоритма BFO.
. BFOA подражает четырем основным механизмам, наблюдаемым в реальной бактериальной системе: хемотаксис, роение, репродукция и ликвидация рассеивания, чтобы решить проблему оптимизации неградиента. Ниже мы представляем формальные нотации, используемые в литературе BFOA, и затем обеспечиваем полный псевдокод алгоритма BFO.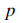 – измерение пространства поиска,
– измерение пространства поиска,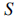 – общее количество бактерий в популяции,
– общее количество бактерий в популяции,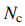 – количество шагов хемотаксиса,
– количество шагов хемотаксиса,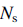 – длина бассейна,
– длина бассейна, – количество шагов репродукции,
– количество шагов репродукции, – число событий ликвидации рассеивания,
– число событий ликвидации рассеивания, – вероятность ликвидации рассеивания,
– вероятность ликвидации рассеивания,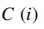 – размер шага в случайном направлении, указывающий на падение.
– размер шага в случайном направлении, указывающий на падение. представляет позицию каждого элемента в популяции бактерий на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. Пусть
представляет позицию каждого элемента в популяции бактерий на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. Пусть 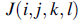 обозначают стоимость расположения i-й бактерии
обозначают стоимость расположения i-й бактерии  (иногда, мы отбрасываем индексы и обращаемся к i-й позиции бактерии как
(иногда, мы отбрасываем индексы и обращаемся к i-й позиции бактерии как  ). Обратите внимание на то, что мы будем взаимозаменяемо именовать J, как 'стоимость' (используя терминологию из теории оптимизации) и как питательную поверхностью (в отношении биологических соединений). Для фактической бактериальной популяции S может быть очень большим (напр. S=109), но p=3. В нашем компьютерном моделировании мы будем использовать намного меньшие численности популяции и сохраним численность популяции фиксированной. BFOA, однако, позволяет брать p>3 так, чтобы мы могли применить метод к задачам оптимизации больших размеров. Ниже, мы кратко описываем четыре главных шага в BFOA.
). Обратите внимание на то, что мы будем взаимозаменяемо именовать J, как 'стоимость' (используя терминологию из теории оптимизации) и как питательную поверхностью (в отношении биологических соединений). Для фактической бактериальной популяции S может быть очень большим (напр. S=109), но p=3. В нашем компьютерном моделировании мы будем использовать намного меньшие численности популяции и сохраним численность популяции фиксированной. BFOA, однако, позволяет брать p>3 так, чтобы мы могли применить метод к задачам оптимизации больших размеров. Ниже, мы кратко описываем четыре главных шага в BFOA. представляет i-ю бактерию на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. C(i) – скаляр, размер шага в случайном направлении, указывающего на падение (выполнение модуля длины). Тогда в вычислительном хемотаксисе движение бактерий могут быть представлены, как
представляет i-ю бактерию на j-м шаге хемотаксиса, k-м шаге репродукции и l-м шаге ликвидации рассеивания событий. C(i) – скаляр, размер шага в случайном направлении, указывающего на падение (выполнение модуля длины). Тогда в вычислительном хемотаксисе движение бактерий могут быть представлены, как

 указывает на вектор единичной длины в случайном направлении.
указывает на вектор единичной длины в случайном направлении.
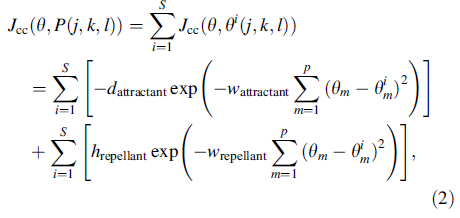
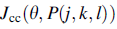 это значение целевой функции, которое будет добавлено к фактической целевой функции (для минимизации), чтобы представить время изменения целевой функции. Коэффициенты
это значение целевой функции, которое будет добавлено к фактической целевой функции (для минимизации), чтобы представить время изменения целевой функции. Коэффициенты 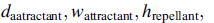 и
и  контролируют силу межклеточной сигнализации. Более конкретно
контролируют силу межклеточной сигнализации. Более конкретно  это глубина аттрактанта, выпущенного ячейкой,
это глубина аттрактанта, выпущенного ячейкой, 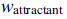 это мера ширины сигнала аттрактанта (квантификация уровня диффузии химиката),
это мера ширины сигнала аттрактанта (квантификация уровня диффузии химиката), 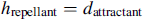 это высота эффекта репеллента (ячейка бактерии также отражает соседнюю ячейку в том смысле, что физически невозможно иметь две ячейки в одном и том же расположении), и
это высота эффекта репеллента (ячейка бактерии также отражает соседнюю ячейку в том смысле, что физически невозможно иметь две ячейки в одном и том же расположении), и