Исследование влияния мультиплексированных каналов и параметров измерений на показатель Херста для трафика пакетов в компьютерных сетях

Введение

Экспериментальные исследования показывают, что потоки в современных сетях не являются простейшими, обладают существенным последействием и самоподобием, носят взрывной характер. По этой причине алгоритмы обработки трафика, предназначенные для работы с простейшим потоком, неэффективны для самоподобных потоков.

Необходимость обеспечения высокого качества обслуживания различных категорий сетевых приложений, учет периодически возникающих задержек в передаче данных и потери пакетов при недостаточной производительности и ограниченных ресурсах памяти делают исследование свойств самоподобного трафика актуальной задачей.

Свойство масштабной инвариантности сетевого трафика позволяет разработать алгоритмы прогнозирования, которые смогут посредством анализа трафика на относительно небольшом отрезке времени предсказать его поведение на более длительных интервалах [1].

Однако на практике проверка потоков на самоподобность и оценка показателя Херста является сложной задачей, поскольку в реальных условиях всегда оперируют конечными наборами данных [2]. Это делает невозможным выявление в коротких трассах трафика фрактальных свойств.

Для оценки степени самоподобия разработано несколько методик. За последние годы резко возросло число исследований потоков сетевого трафика с помощью метода нормированного размаха.

Описание моделируемой сети

Сеть, на которой проводился анализ пакетного трафика, состоит из узлов-генераторов самоподобного трафика (n(100) – n(199)), шлюза (1), маршрутизатора (2), а также узла-приемника (3).

Сетевой трафик создается сотней независимых отдельных источников, которые передают данные с одинаковой интенсивностью, но с длительностями ON/OFF интервалов, распределенными в соответствии с тяжелохвостым распределением.

Каждый источник генерирует пакеты данных с постоянной битовой скоростью  20000 бит/с, размер пакета составляет 128 байт. Длительности ON и OFF периодов являются случайными величинами, которые распределены по закону Парето и задаются средними значениями 0,5 с и 1,5 с соответственно. Параметр формы распределения равен 1,2 (типичное значение).

Топология данной сети показана на рисунке 1.

Рисунок 1 – Топология моделируемой сети

Мы исследуем свойства трафика на входе маршрутизатора. Пример профиля этого сетевого трафика, полученного в результате мультиплексирования 100 ON/OFF источников, показан на рисунке 2.

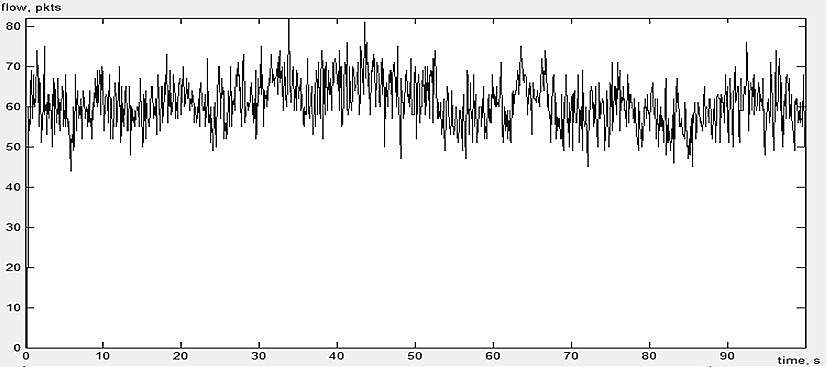
Рисунок 2 – Сетевой трафик при мультиплексировании 100 ON/OFF источников

В этом эксперименте измерение числа принятых маршрутизатором пакетов производилось на временном интервале длиной 100 с от начала моделирования с временным разрешением, равным 0,1 с.

Влияние параметров измерений на показатель Херста

Для оценки степени самоподобия исследуемого сетевого трафика применялась методика нормированного размаха, рассмотренная в [3].

Согласно данной методике, исходной величиной в исследовании свойств пакетного трафика моделируемой сети является временной ряд 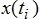– набор измерений числа пакетов, поступивших на вход маршрутизатора в интервале времени между измерениями. Данные измерения производились в дискретные моменты времени

Важнейшим параметром,  характеризующим  степень  самоподобия  ряда,  является  показатель Херста H, который описывается следующим эмпирическим соотношением

где a – константа, R – размах отклонения значений ряда x от его среднего значения, S – стандартное отклонение x.

Пусть  – среднее значение случайной величины, тогда стандартное отклонение x определяется из формулы

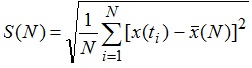
Обозначим через

накопившееся отклонение значений случайной величины 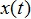 от ее среднего значения за время t.

Разность между максимальным и минимальным значениям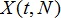и при называется размахом .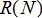

Изменение величины показателя Херста в зависимости от длины временного интервала отображено на рисунке 3.

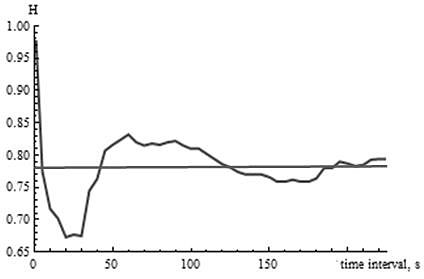
Рисунок 3 – Зависимость показателя Херста от длины временного интервала

Из графика видно, что показатель Херста в значительной мере зависит от длины временного интервала. Вначале при небольшом значении длины наблюдается резкое убывание, а затем некоторое возрастание степени самоподобия. С увеличением длины интервала амплитуда колебаний показателя Херста относительно математического ожидания затухает. Это подтверждают и исследования, проведенные в [4].

Отсюда следует, что для определения степени самоподобия сетевого трафика с высокой достоверностью, необходимо увеличить длительность сбора сведений о трафике в исследуемой сети.

В нашем случае установившееся среднее значение показателя Херста равно 0,78.

Зависимость показателя Херста от величины временного разрешения показана на рисунке 4а и 4б.

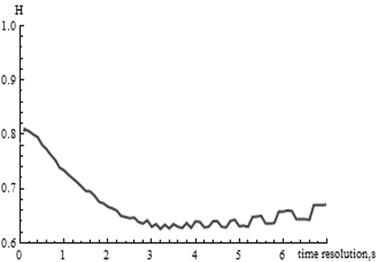
Рисунок 4 – Зависимость показателя Херста от величины временного разрешения:
а) График с приращением временного разрешения 0,1 с;
б) График с приращением временного разрешения 1 с

Из графиков видно, что при значениях временного разрешения, не превышающих 5 с, происходит убывание показателя Херста. С увеличением длины интервалов между измерениями наблюдается периодическое возрастание показателя Херста, которое сопровождается ростом амплитуды и уменьшением частоты колебаний.

Следовательно, для измерения степени самоподобия трафика с высокой точностью следует использовать малые значения временного разрешения, которые согласуются с интенсивностью поступления пакетов. Например, модель трафика, профиль которого показан на рисунке 2, была получена при временном разрешении 0,1 с, что обеспечило высокий уровень усреднения и позволило получить достоверные статистические данные.

Таким образом, при различных значениях длительности измерений трафика и величины интервалов между измерениями оценка степени самоподобия сетевого трафика может колебаться. Следовательно, для адекватного сравнения нескольких потоков по критерию самоподобия необходимо иметь фиксированные значения параметров измерений.

Вместе с тем, проведенные исследования показали, что изменение параметров измерений не влечет за собой качественного изменения показателя Херста. Это означает, что для выявления наличия самоподобия сетевого трафика не требуется длительного сбора сведений о трафике и высокой частоты измерений.

Влияние мультиплексированных каналов на показатель Херста

Эксперименты с изменением количества мультиплексированных каналов показали, что зависимость показателя Херста от числа потоков самоподобного трафика является нелинейной, имеет сложную колебательную природу (рисунок 5). Оценка полученного ряда при помощи методики нормированного размаха показала наличие ярко выраженной степени самоподобия.

Рисунок 5 – Зависимость показателя Херста от числа мультиплексированных потоков

Выводы

Исследована зависимость показателя Херста от длины временного интервала и временного разрешения. Изучено влияние параметров измерений на качество оценки степени самоподобия трафика. Показана зависимость степени самоподобия трафика от числа мультиплексированных потоков.

Показано, что изменение параметров измерений не влечет за собой качественного изменения показателя Херста. Это означает, что для выявления наличия самоподобия сетевого трафика не требуется длительного сбора сведений о трафике и высокой частоты измерений.

Выявленные свойства показателя Херста следует учитывать при проведении анализа сетевого трафика с применением методики нормированного размаха.

Литература

1. Бельков Д.В. Актуальность исследования фрактального трафика / Д.В. Бельков // Материалы IV международной научно-практической конференции «Постигането на висшето образование – 2008» – Т. 12. – С. 44-46.
2. Шелухин О.И. Мультифракталы. Инфокоммуникационные приложения / О.И. Шелухин – М.: Горячая линия – Телеком, 2011. – 576 с.
3. Моргайлов Д.Д., Ладыженский Ю.В., Юнис М. Моделирование самоподобного входного трафика сетевых процессоров в системе NS-2 / Д.Д. Моргайлов, Ю.В. Ладыженский, М. Юнис // Материалы III международной научно-технической конференции «Информационные управляющие системы и компьютерный мониторинг – 2012». – Донецк, 2012. – С. 826-832.
4. Калуш Ю.А., Логинов В.М. Показатель Херста и его скрытые свойства / Ю.А. Калуш, В.М. Логинов // Сибирский журнал индустриальной математики. – 2002. – Т. 5, № 4 (12). – С. 29-34.