Моделирование самоподобного входного трафика сетевых процессоров в системе NS-2
Автор: Ю.В. Ладыженский, Д.Д. Моргайлов, М. Юнис
Источник: Ладыженский Ю.В., Моргайлов Д.Д., Юнис М. Моделирование самоподобного входного трафика сетевых процессоров в системе NS-2 / Ю.В. Ладыженский, Д.Д. Моргайлов, М. Юнис // Наукові праці ДонНТУ. – Донецк, 2012. – (Серия «Інформатика, кібернетика та обчислювальна техніка»). – № 16 (204). – С. 68-74.
Аннотация
Ю.В. Ладыженский, Д.Д. Моргайлов, М. Юнис. Моделирование самоподобного входного трафика сетевых процессоров в системе NS-2. Проведены анализ и оценка функциональных возможностей и качества моделирования трафика сетевых процессоров в системе NS-2. Рассмотрены основные свойства самоподобного трафика и методика оценки степени самоподобия. Выполнено экспериментальное моделирование самоподобного трафика в системе NS-2 и исследованы его свойства.
Ключевые слова: сетевой процессор, самоподобный сетевой трафик, симулятор NS-2, моделирование.
Y.V. Ladyzhesky, D.D. Morgajlov, M. Younis. Simulation of self-similar input traffic for network processors using NS-2 system. The analysis and evaluation of functionality and simulation quality of input traffic for network processors using NS-2 system are made. The main properties of self-similar traffic and estimation method of assessing the self-similarity degree is shown. Self-similar traffic experimental simulation is done using NS-2 system and it’s properties are researched.
Keywords: network processor, self-similar network traffic, NS-2 simulator, simulation.
Введение
Сетевые процессоры в настоящее время активно используются на различных уровнях стека протоколов. Сетевые процессоры должны обеспечивать маршрутизацию огромных высокоскоростных потоков пакетов в ядре Интернета. Программируемость архитектуры, возможности параллельной и конвейерной обработки позволяют расширить области применения многоядерных сетевых процессоров. Для эффективного выбора параметров архитектуры, разработки быстрых адаптируемых алгоритмов анализа пакетов, оптимального использования ресурсов сетевого процессора важным является исследование свойств входных потоков, поступающих в процессор на обработку. Экспериментальные исследования показывают, что потоки в современных сетях не являются простейшими, обладают существенным последействием и самоподобием.
Необходимость обеспечения сетевыми процессорами высокого качества обслуживания различных категорий сетевых приложений, учет периодически возникающих задержек в передаче данных и потери пакетов при недостаточной производительности и ограниченных ресурсах памяти делают исследование свойств самоподобного трафика актуальной задачей.
Свойство масштабной инвариантности сетевого трафика позволяет разработать алгоритмы прогнозирования, которые смогут посредством анализа трафика на относительно небольшом отрезке времени предсказать его поведение на более длительных интервалах [1].
Целью данного исследования является разработка модели входного трафика сетевых процессоров для имитационно-аналитической системы оценки эффективности архитектур сетевых процессоров.
Задачами исследования являются анализ и экспериментальная оценка функциональных возможностей и качества моделирования сетевого трафика в системе NS-2.
Самоподобие трафика
Многочисленные современные исследования Интернет трафика свидетельствуют о том, что он обладает свойством самоподобия [2].
Под самоподобием подразумевается повторяемость распределения нагрузки во времени при различных масштабах [3]. Если набор значений самоподобной функции (проявляющей признаки самокорреляции) разделить на равные группы, а затем просуммировать значения внутри групп, то набор сумм будет подчиняться той же самой корреляционной функции, что и исходные данные [3].
В отличие от пуассоновских самоподобные процессы характеризуются наличием последействия: вероятность наступления очередного события зависит не только от времени, но и от предыдущих событий (предыстории) [2]. Это означает, что число текущих событий может зависеть от числа предыдущих событий в отдаленные промежутки времени [2]. Поэтому одним из основных свойств самоподобного процесса является медленно убывающая зависимость между объемами трафика в разные моменты времени.
Самоподобный процесс часто носит взрывной (burst) характер, что проявляется в наличии выбросов при относительно низкой скорости потока событий [2]. Эти локализованные во времени скопления (congestions) вызывают значительные потери пакетов, даже когда суммарная потребность в обслуживании всех потоков далека от максимально допустимых значений [3], поскольку расчеты требуемых характеристик современных сетей используют лишь усредненные свойства трафика. В частности, для самоподобного потока пакетов при увеличении размера буфера на входе сетевого процессора вероятность потерь падает значительно медленнее, чем для экспоненциального закона, используемого в классических моделях телетрафика [4]. Алгоритмы обработки трафика сетевым процессором, предназначенные для работы с простейшим потоком, неэффективны для самоподобных потоков.
Возможные причины самоподобия сетевого трафика – в особенностях распределения файлов по серверам, их размерах, а также в типичном поведении пользователей [3]. Изначально не проявляющие свойств самоподобия потоки данных, пройдя обработку на узловых серверах и активных сетевых элементах, начинают проявлять ярко выраженные признаки самокорреляции [3].
Важнейшим параметром,
характеризующим степень самоподобия, является параметр Херста H, определяемый для временного ряда 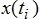 , ti – дискретные
моменты времени,
, ti – дискретные
моменты времени, 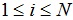 . Параметр Херста описывается эмпирическим соотношением
. Параметр Херста описывается эмпирическим соотношением

где a – константа, R – размах отклонения значений ряда x, S – стандартное отклонение x.
Пусть  – среднее значение случайной величины
– среднее значение случайной величины
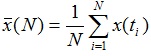
Стандартное отклонение x определяется из формулы
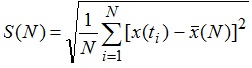
Обозначим через

накопившееся отклонение значений случайной величины x(t) от ее среднего значения  за время t.
за время t.
Разность между максимальным и минимальным значениями 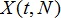 называется размахом
называется размахом
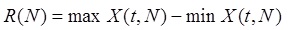
где 
Генерация самоподобного трафика в системе NS-2
NS (Network Simulator – сетевой симулятор) – инструмент для моделирования процессов в компьютерных сетях [5]. Он позволяет описать для моделируемой сети топологию, конфигурацию источников и приемников трафика, параметры соединений (полосу пропускания, задержку, вероятность потери пакетов) и другие параметры. При моделировании имеется возможность управлять параметрами буферов, проводить мониторинг принятых, отправленных и потерянных пакетов, осуществлять сбор статистики и др. С помощью генерации выходных trace-файлов может быть получена информация о динамике трафика, состоянии соединений и объектов сети, а также работе протоколов [5].
Для генерации трафика в системе NS-2 предназначены объекты типа Traffic. Они создаются методами Traffic/type, где type – Expoo, Pareto или Trace [5].
Объект Traffic/Pareto – ON/OFF генератор трафика согласно распределению Парето.
Простая ON/OFF модель предполагает, что источники переключаются между двумя состояниями: ON-состояние, в котором источники генерируют трафик с постоянной скоростью, OFF-состояние, в котором они молчат [6].
На рисунке 1 показан пример создания генератора трафика Парето.

Рисунок 1 – Пример создания генератора трафика Парето
Созданный объект генерирует пакеты размером 128 байт с постоянной битовой скоростью 20000 бит/с в течение ON-периода со средней продолжительностью в 500 мс. Средняя длительность OFF-периода составляет 1,5 с, параметр формы (характеризует, будет ли распределение иметь конечное или бесконечное среднее и дисперсию) равен 1,2 (типичное значение).
При постоянном размере пакетов ON и OFF периоды распределены по закону Парето.
Распределение Парето имеет функцию распределения
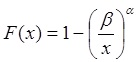
где 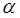 – параметр формы,
– параметр формы,  – минимальное
значение случайной величины x.
– минимальное
значение случайной величины x.
Плотность распределения Парето задается функцией
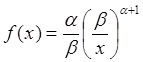
при x > и
и 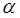 > 0,
> 0,
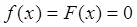
при x ≤ .
.
Среднее значение случайной величины определяется из формулы
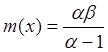
Параметр 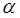 определяет среднее и дисперсию случайной величины:
определяет среднее и дисперсию случайной величины:
– если 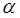 ≤ 1, распределение имеет бесконечное среднее;
≤ 1, распределение имеет бесконечное среднее;
– если 1 ≤ 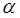 ≤ 2, распределение имеет конечное среднее и бесконечную дисперсию;
≤ 2, распределение имеет конечное среднее и бесконечную дисперсию;
– если 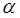 ≤ 2, распределение имеет бесконечную дисперсию.
≤ 2, распределение имеет бесконечную дисперсию.
Существует отношение между параметром 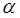 и параметром Херста H
и параметром Херста H

Создание и исследование моделей самоподобного трафика в системе NS-2
Моделируемая сеть состоит из узлов-генераторов самоподобного трафика (n(100) – n(199)), шлюза на сетевом процессоре (1), маршрутизатора на сетевом процессоре (2), а также узла-приемника (3). Топология сети показана на рисунке 2.

Рисунок 2 – Моделируемая топология
Сетевой трафик в моделируемой сети создается сотней независимых отдельных источников, которые передают данные с одинаковой интенсивностью, но с длительностями, распределенными в соответствии с тяжелохвостым распределением [6].
Каждый источник генерирует трафик с постоянной битовой скоростью 20000 бит/с, размер пакета составляет 128 байт. Длительности ON и OFF периодов являются случайными величинами с распределением Парето и задаются средними значениями 0,5 с и 1,5 с соответственно. Минимальные длительности составляют 0,0833 с для ON периода и 0,25 с для OFF периода. Параметр формы распределения равен 1,2.
На рисунках 3 и 4 приведены графики функций распределения и плотности распределения Парето для ON периода соответственно.
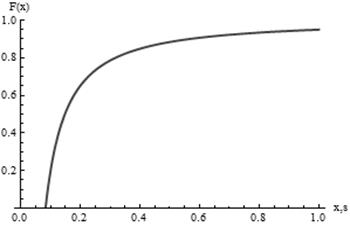
Рисунок 3 – График функции распределения Парето для ON периода
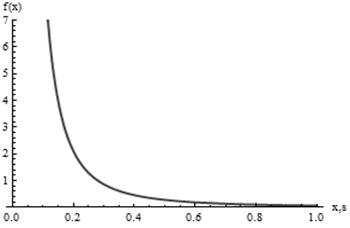
Рисунок 4 – График функции плотности распределения Парето для ON периода
На рисунках 5 и 6 приведены графики функций распределения и плотности распределения Парето для OFF периода соответственно.

Рисунок 5 – График функции распределения Парето для OFF периода
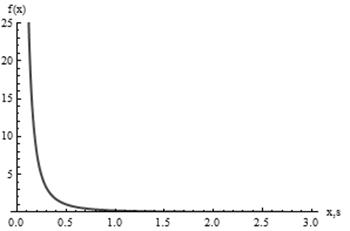
Рисунок 6 – График функции плотности распределения Парето для OFF периода
Смоделированный трафик был получен при временном разрешении 0,1 с, что обеспечивает высокий уровень усреднения. Это позволяет получать достоверные статистические данные.
Трафик, генерируемый одним источником в течение 10 с, 100 с и 5000 с, приведен на рисунках 7, 8 и 9 соответственно в виде зависимости числа принятых шлюзом пакетов в единицу времени.

Рисунок 7 – Трафик, генерируемый одним источником в течение 10 с

Рисунок 8 – Трафик, генерируемый одним источником в течение 100 с

Рисунок 9 – Трафик, генерируемый одним источником в течение 5000 с
Выполним оценку показателя Херста при помощи методики R/S статистики (нормированного размаха), рассмотренной ранее. С этой целью была разработана программа на языке C#, реализующая данный расчет на основании результатов моделирования и выполняющая построение гистограммы временного ряда в пакете Excel. Для приведенной модели трафика на временном интервале 100 с данный показатель равен 0,86. Поскольку H > 0,5, исследуемый поток пакетов имеет персистентную природу (самоподдерживающийся поток), обладает длительной памятью и является самоподобным.
Профиль сетевого трафика, полученного при мультиплексировании 100 ON/OFF источников на временном промежутке от 0 до 100 с, показан на рисунке 10.
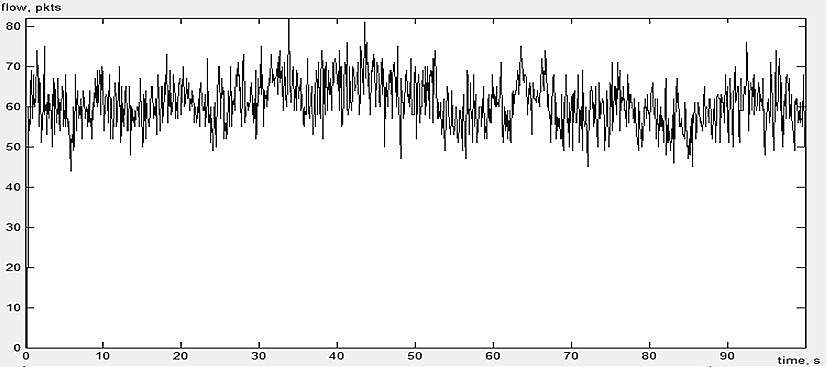
Рисунок 10 – Сетевой трафик для мультиплексирования 100 ON/OFF источников
Приведенная зависимость была получена путем измерения числа принятых пакетов на сетевом процессоре-маршрутизаторе в единицу времени (0,1 с).
Исследуемый самоподобный процесс не обладает значительной пачечностью, которая измеряется отношением пиковой интенсивности процесса поступления заявок к его среднему значению. Это отличает рассматриваемый поток от реальных аналогов.
Параметр Херста для полученной модели трафика равен 0,81.
Гистограмма для временного ряда, отражающая плотность распределения числа пакетов в единицу времени, приведена на рисунке 11.
Визуально гистограмма похожа на распределение Пуассона, однако полученное значение показателя Херста опровергает это предположение. Следовательно, распределение трафика близко к пуассоновскому, но им не является. Установленную близость можно объяснить наличием большого числа мультиплексированных потоков пакетов.
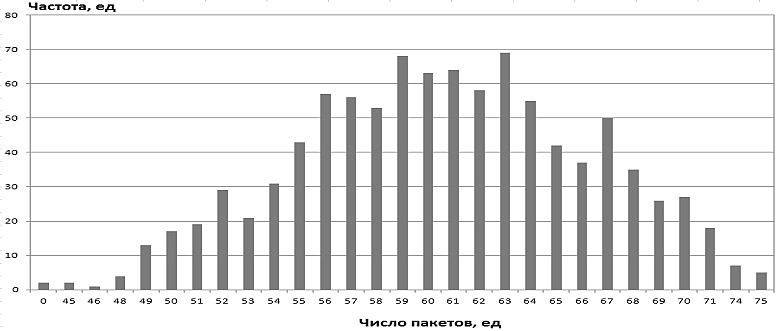
Рисунок 11 – Гистограмма временного ряда
Зависимость параметра Херста от числа мультиплексированных потоков самоподобного трафика показана на рисунке 12.
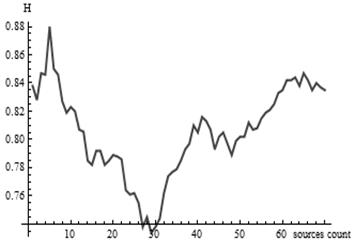
Рисунок 12 – Зависимость параметра Херста от числа мультиплексированных потоков
Оценка полученного ряда при помощи методики нормированного размаха показала, что данная зависимость обладает ярко выраженной степенью самоподобия (Н = 0,93).
Заключение
Разработаны имитационные модели самоподобного трафика пакетов, порождаемого одним источником и мультиплексированного трафика пакетов.
Разработан скрипт в системе NS-2 на языке Tcl, предназначенный для моделирования самоподобного сетевого трафика, генерируемого заданным числом независимых источников.
Разработана программа на языке C#, реализующая расчет показателя Херста на основании результатов моделирования, представленных в виде trace-файла, и выполняющая программное построение гистограммы временного ряда в пакете Excel.
Проведены эксперименты на созданных моделях и выполнена оценка показателя самоподобия. Построена гистограмма временного ряда для мультиплексированного трафика.
Научная значимость данной работы состоит в разработке имитационных моделей входного трафика пакетов сетевых процессоров.
Практическая ценность выполненных исследований состоит в создании скриптов, моделирующих потоки с заданными свойствами.
Наличие в системе NS-2 интерфейсов расширения позволяет создавать комбинированные имитационные и имитационно-аналитические модели сетевых процессоров с применением объектно-ориентированных языков высокого уровня. Это является одним из направлений дальнейших исследований.
Список литературы
- Бельков Д.В. Актуальность исследования фрактального трафика / Д.В. Бельков // Материалы IV Mеждународной научно-практической конференции «Постигането на висшето образование – 2008» – Т. 12. – С. 44-46.
- Статистические свойства интернет трафика [Электронный ресурс]. Режим доступа: http://www.nag.ru/goodies/articles/sst/sst.html
- «Фрактальная катастрофа» TCP/IP [Электронный ресурс]. Режим доступа: http://itc.ua/articles/_fraktalnaya_katastrofa_tcp_ip_5571/
- Зюльков И.А. Самоподобные свойства трафика систем с повторными вызовами / И.А. Зюльков // Вестник ВГУ. – 2002. – (Серия «Физика, математика»). – № 1. – С. 20-26.
- Network Simulator (Сетевой симулятор ns2) [Электронный ресурс]. Режим доступа: http://telematika.stu.neva.ru/FILES/KAFEDRA/STUDENTS/POSOBIE/ns-old-html/ns-old.htm
- Шелухин О.И. Мультифракталы. Инфокоммуникационные приложения / О.И Шелухин – М.: Горячая линия – Телеком, 2011. – 576 с.