Визуализация и анализ многомерных данных

с использованием пакета NovoSpark^® Visualizer

 

Дмитрий Эйдензон, к.т.н., Корпорация NovoSpark, Ватерлоо, Канада, dmitri.eidenzon@novospark.com

Дима Шамрони, Корпорация NovoSpark, Ватерлоо, Канада, dima.shamroni@novospark.com

Виталий Воловоденко, к.т.н., доцент, ОСУ АВТФ ТПУ, Томск, Россия, vitali.volovodenko@novospark.com

 

Аннотация

 

Традиционные методы визуализации многомерных данных (множественные диаграммы рассеивания, полярные координаты, лица Чернова и другие) обладают известным недостатком: невозможностью отобразить всю многомерную информацию, как статическую, так и динамическую, в едином образе. В статье рассматривается метод визуализации и качественного анализа многомерных данных, реализованный в программном обеспечении NovoSpark^® Visualizer и обсуждаются различные области применения метода.

 

Метод Визуализации

 

Основой визуализационного подхода является линейное преобразование значений многомерного наблюдения A в двумерную кривую  f_A(t), т.е. A ↔ f_A(t), при этом гарантируется, что близким по значениям наблюдениям A  и B будут соответствовать визуально близкие образы-кривые f_A(t) и f_B(t);  для сильно различающихся по значениям наблюдений их образы-кривые будут заметно отличаться.

 

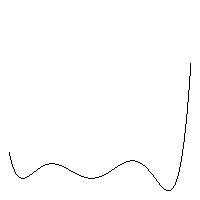
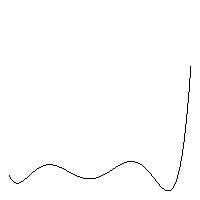
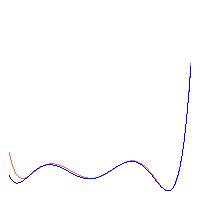
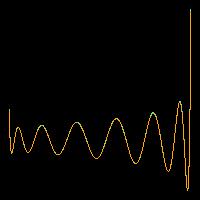
Образы  двух 7-ми мерных наблюдений A = {1, 2, 3, 4, 5, 6, 7} и B = {0, 3, 2, 5, 4, 7, 6} показаны на Рисунке 1 ниже:

 

Образ наблюдения A↔ fA(t)	Образ наблюдения B↔ fB(t)	Образы наблюдений A и B: fA(t) и fB(t)

Рисунок 1. Двумерные образы многомерных наблюдений

 

Введение понятия расстояния между наблюдениями позволяет отображать наблюдения в трехмерном пространстве, отображая значения величины расстояния на «z-оси». Метрика расстояния выбирается произвольно и соответствует, например, геометрическому (Евклидовое), статистическому (Махаланобис) или хронологическому (временной промежуток) расстояниям. Таким образом появляется возможность отображения как статических, так и динамических данных.

 

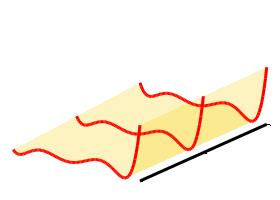
В силу линейности преобразования A ↔ f_A(t), образу отрезка прямой между многмерными наблюдениями A и B соответсвует поверхност, соединяющая образы наблюдений. Любая кривая, представляющая наблюдение с промежуточными значениями, будет лежать на этой поверхности, как это показано на Рисунке 2.

Наблюдения A и B в трехмерном изображении.	Отрезок между наблюдениями A и B с промежуточным наблюдением.

Рисунок 2. Изображение отрезка многомерной прямой.

 

Для болле детального сравнения наблюдений, особенно в случае неоднородных единиц измерения показателей, данные можно трансформировать одним из традиционных способов:

·        нормализация - для выражения результатов в единой системе измерений

·        стандартизация - для сравнения переменных и/или наборов данных с различными характеристиками распределения или единицами измерения

 

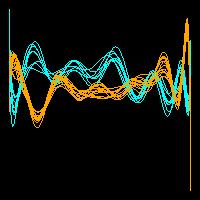
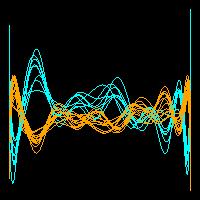
Операция трансформирования детализирует образы данных, что позволяет успешнее идентифицировать закономерности, если таковые имеются.  На Рисунке 3 показаны два 15-ти мерных набора данных и влияние трансформации наблюдений на их образы.

 

Нетрасформированные данные	Нормализованные данные	Стандартизованные данные

Рисунок 3. Влияние трансформации данных  на образы наблюдений.

 

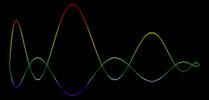
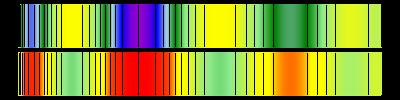
Чтобы подчеркнуть различия между образами наблюдений используется цветная палитра,  акцентирующая уровни изменения значений кривых. Производя  воображаемое растяжение кривых вдоль Z-оси и глядя сверху на результат этой операции, можно получить цветные полоски, представляющие собой спектр каждого наблюдения. На Рисунке 4 показаны образы стандартизованных наблюдений A и B  и соответствующие им спектральные полоски.

 

Рисунок 4.  «Спектры» многомерных наблюдений

Приложения

 

Рассматриваемый метод визуализации нашел широкое применение практически на всех  стадиях обработки и качественного анализа многомерных данных. Например, выявление аномалий и значимых переменных на этапе подготовки данных;  идентификация закономерностей посредством кластеризации наборов статических данных и определение периодических участков в динамических данных (процессах); выбор и сравнение эталонных экземпляров среди  одиночных наблюдений и групп наблюдений.

 

Рассматриваемый метод и программное обеспечение (NovoSpark® Visualizer) успешно применяется для принятия управленческих решений в системе энергоснабжения Томской области,  в клинических исследованиях НИИ Онкологии РАМН, и других отраслях.

 

Выявление Аномалий

 

Аномальные наблюдения определяются как по форме их образов (визуально значимые различия в образах указывают на различия в оригинальных данных), так  и через «облако» многомерного интервала. Если образ  наблюдения полностью вписывается в облако интервала, то соответствующие этому образу значения параметров наблюдения находятся между минимальной и максимальной границами заданного интервала по всем измерениям, как это показано на рисунке справа.

 

Сравнение Эталонов

 

В качестве эталонных наблюдений для статических данных рекомендуется выбирать многомерные средние значения кластеров или группы наиболее представительных наблюдений кластеров.  Так же, для определенного класса задач, многомерный интервал может рассматриваться в качестве границ эталонного экземпляра.

 

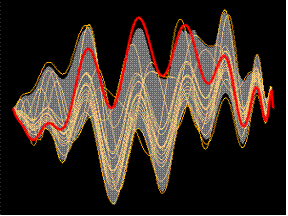
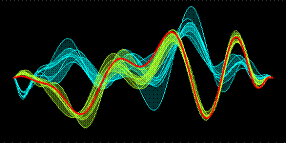
На рисунке слева визуализируется сравнение многомерного наблюдения с группами эталонов (показаны зеленым и синим цветами) по формам образов. Образ диагностируемого наблюдения показан красным цветом – очевидно, что наблюдение значительно ближе к «зеленой» эталонной группе.

 

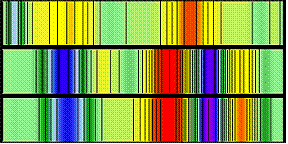
Сравнение эталонов по визуальной близости спектров наблюдений показано на рисунке справа - спектры наблюдений (сверху вниз) соответствуют синему, зеленому и красному наблюдениям из примера выше – два нижних спектра более похожи друг на друга и значительно отличаются от верхнего.

Динамические Данные

 

Выявление закономерностей в динамических данных (процессах) для построения моделей прогноза поведения многопараметрических систем является сложной и, зачастую, невыполнимой задачей. Визуализация значительно упрощает и ускоряет определение периодических участков процесса, однозначно указывая на временные интервалы с однородным поведением системы. 

 

Процессы изображаются в виде трехмерных поверхностей (двумерные образы состояний просесса, упорядоченные на временной оси). Так на Рисунке 5 показаны образы двух коррелирующих процессов: замеры потребления энергии за неделю (сверху) и внешние факторы, определяющие нагрузку энергосистемы (снизу). Отчетливо видны периодически повторяющиеся участки: пять дней рабочей недели и два выходных дня.

 

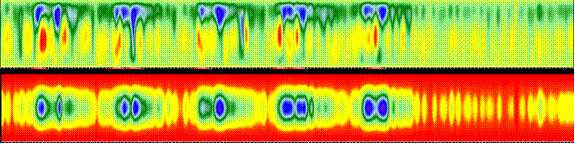
Рисунок 5.  Идентификация закономерностей в  динамических данных

 

Пример. Электрокардиограмма.

 

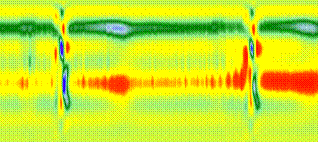
	В примере используются данные измерений 12-ти  канальной электрокардиограммы. Для иллюстрации возможностей метода на рисунке слева показаны изображения, полученные традиционным (сверху) и рассматриваевым в этой статье (снизу) способами.   Рисунок снизу иллюстрирует детальные различия между двумя последовательными сокращениями сердечной мышцы.

 

Список литературы

 

1.      http://www.novospark.com Интернет страница Корпорации NovoSpark^®.

 

Multidimensional Data Visualization and Analysis

With NovoSpark^® Visualizer

 

Dmitri Eidenzon, Ph.D., NovoSpark Corporation, Waterloo, Canada, dmitri.eidenzon@novospark.com

Dima Shamroni, Ms. Sc., NovoSpark Corporation, Waterloo, Canada, dima.shamroni@novospark.com

Vitali Volovodenko, Ph.D., professor, OSU AVTF TPU, Tomsk, Russia, vitali.volovodenko@novospark.com

 

Abstract

 

Traditional methods of multidimensional data visualization (such as scatter plot matrices, polar coordinates, Chernoff Faces etc.) lack the ability to simultaneously display all dimension values, static or dynamic, in a clear single image. In this paper the authors introduce a method for visualization and qualitative analysis of multivariate data implemented in the NovoSpark® Visualizer software. Various applications are discussed as well.