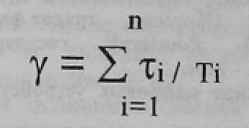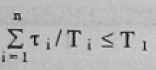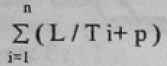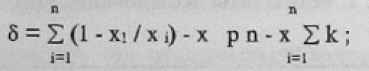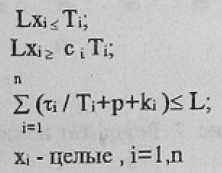Назад в библиотеку
Оптимизация планирования цикла реального времени вычислительной системы
Автор: Иванов А. Ю.
Источник: Наукові праці Донецького національного технічного університету, серія «Інформатика, кібернетика та обчислювальна техніка»,випуск 1, Донецк, ДонНТУ, 1997, стор. 198-201
Abstract
Ivanov A. Optimal planning of real-time circle of computer system. This article deals with design computer calculations in real-time for the special system. Algoritm planning of real-time circle has been developed and researched.
Введение
Проектирование систем реального времени в том числе и для полунатурного моделирования требует обоснованного выбора как технических средств достаточного быстродействия так и оснащения их соответствующими программами обработки и управления. Одним из критериев эффективности систем управления и моделирования динамическими объектами является загрузка цифровой части, обеспечивающей непрерывность управления. Повышение загрузки процессоров позволяет расширять круг решаемых задач и принимать проектные решения по совершенствованию вычислительных систем.
В системах с обратной связью решение задач осуществляется путем многократного повторения циклов управления, когда фазовые переменные объекта изменяются в заданном темпе вычислений. Критерий цикла реального времени записывается [1]:
где ti — установленное на основании системных измерений время выполнения на ЭВМ потока (программы) вычисления i-ой фазовой переменной; Ti — требуемый период вычисления i-ой фазовой переменной.
Использование распараллеливания и совмещения вычислительных процессов требует создания алгоритмов планирования вычислений, минимизирующих время выполнения цикла реального времени. Сложные объекты моделирования имеют до 40 [2] существенно отличающихся по частоте изменения фазовых переменных. Для заданной вычислительной системы по исходным Ti можно определить минимальное необходимое быстродействие в режиме реального времени:
Если
то критерий существования допустимого расписания потоков переписывается [3]:
В случае если Т1 = НОД {Тi}, i= 1,n. фазовые переменные вычисляются неравномерно на Т1. Если выбрать L = НОД { Т, } и р-накладные расходы на переключение с выполнения потока вычисления одной фазовой переменной на другую то (1) запишется:
где: L/Ti= 1/xi — часть времени ti выполнения потока вычисления i-ой фазовой переменной на L;
время занятости периода L всеми n потоками;
Т1 / L = хi — сколько раз L повторяется на Т1;
сколько времени на Т1 ЭВМ занята решением задачи моделирования.
Величина L может быть определена по алгоритму Эвклида. Выигрыш во времени по сравнению с планированием по минимальной частоте (Т1) составит:
где: ki — максимальное время выполнения блокируемого от прерываний программно - временного устройства (ПВУ) i-ой программы.
Данное представление организации вычислительного процесса моделирования предопределяет два основных алгоритма планирования потоков вычислений для циклической системы заданий с крайними сроками: равномерный и неравномерный. Разработанный алгоритм планирования работает как для заданной тактовой частоты программно-временного устройства (внешний или таймер ПЭВМ), так
и выдаст рекомендации по структуре и разрядности синхронизатора. Известное положение численного анализа алгоритмов определения L свидетельствует о том что в 61% экспериментов при случайно взятых Ti, значение L получается равным 1. Следовательно непроизводительные затраты на переключение с вычисления одной фазовой переменной на другую тем меньше, чем больше L, поскольку число прерываний программно-временного устройства постоянно и равно L. Величина L может быть увеличена уменьшением отдельных Тi, учитывая что Тi=Lxi. Математической основой разработанного на ПЭВМ для системы реального времени планировщика является предложенный алгоритм оптимизации периода синхронизации вычислений фазовых переменных. Задача оптимизации относится к классу задач нелинейного целочисленного программирования и записывается в виде:

при системе ограничений:
где : ki — время выполнения блокируемого от прерываний ПВУ участка i-ой программы; с — величина допуска изменения Ti.
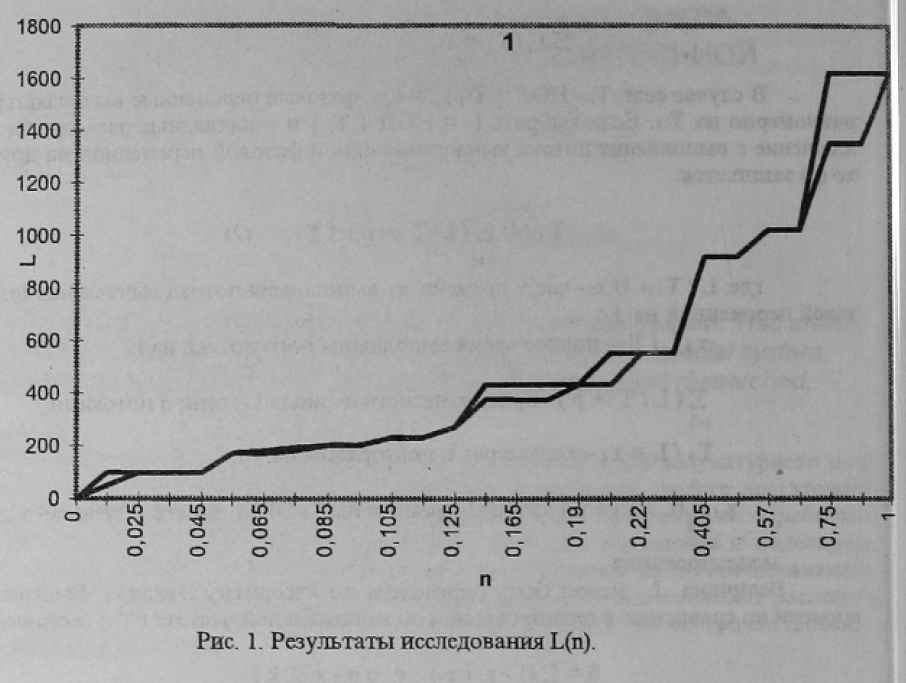
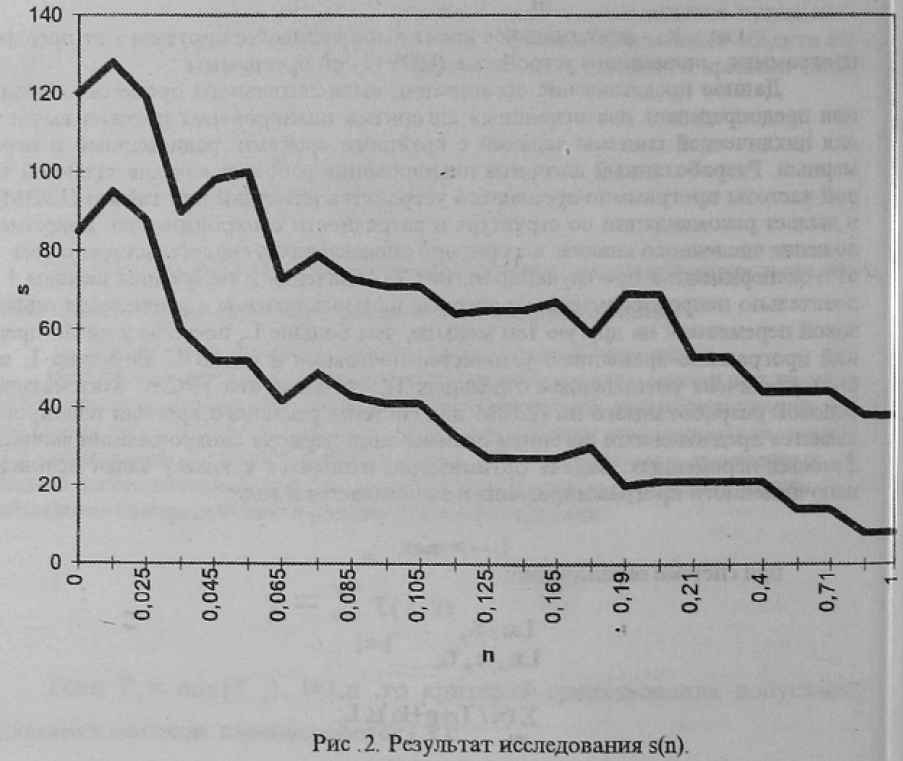
В систему ограничений может быть введено дополнительно условие выигрыша по сравнению с одночастотной организацией ВП. В результате ее решения методом ветвей и границ, учитывающем специфику постановки задачи оптимизации получаем исходную информацию для планирования. Эффективность разработанного алгоритма оптимизации реализованного на языке С была проверена экспериментально на программных моделях для ПЭВМ. На вход алгоритма подавались различной размерности последовательности простых чисел и чисел Фиббоначи. При этом исследовались зависимости величин L, числа итераций (s) алгоритма оптимизации от размерности (n) задачи и величины с. Графики зависимостей s = f (n) и L = f (n) для одной из последовательностей приведены на рис.1, 2. Анализ экспериментов позволяет сделать следующие выводы :
- наиболее существенно на величину L (мажорантой является гипербола) влияет Т2 - Т1;
- при с >= 0.03 величина s зависит только от n и прямо пропорциональна ей;
- изменение только с, практически не влияет на величину s;
- при одновременном изменении ci величина s прямо пропорциональна ci и n;
- величина L прямо пропорциональна Т, обратно пропорциональна сi и практически не зависит от n;
- при небольшом отличии Тi, и Тi+1 целесообразно их объединить (t + t(i+1)).
Заключение
В заключение следует отметить что предложенная методика планирования многочастотных вычислительных процессов увеличивает резервы цифровой части по расширению класса решаемых задач моделирования и управления сложными динамическими системами. Результаты планирования равномерного расписания достаточно просто учитываются диспетчером обработки прерываний от ПЭВМ, в отличие от списочного расписания при неравномерном алгоритме. При реализации алгоритма в виде внешнего ПВУ аппаратные затраты также более низкие чем при плановой инициализации за счет упрощенного арбитрирования запросов циклограмм в реальном времени.
Литература
1. Пьявченко О Н., Суржснко И.Ф., Шаповал В.Г. Технология подготовки задач полу-натурного моделирования при исследовании и проектировании сложных систем управления движением объектов. - Теория и применение моделирующих систем (труды). К. Наукова думка, 1986 г.
2. Виттах В.А., Цыбатов В. А. Оптимизация бортовых систем сбора и обработки данных. - М. : Наука, 1985 г.
3. Иванов А.Ю., Святный В.А. Алгоритм организации цифровых вычислении в цикле реального времени АЦВС. - Вопросы радиоэлектроники Сср.ЭВТ. Вып.2,1986г.