
Источник: Министерство образования Российской Федерации. Новосибирский государственный университет. Учебное пособие. Издательство Новосибирского госуниверситета. Новосибирск. 1998 г.
Министерство образования Российской Федерации
Нижегородский государственный университет
им. Н.И. Лобачевского
В. П. Гергель, Р. Г. Стронгин
Учебное пособие
Издание 2-е, дополненное
Издательство Нижегородского госуниверситета Нижний Новгород 2003
Аннотация
В учебном пособии излагается учебный материал, достаточный для успешного начала работ в области параллельного программирования. Для этого в пособии дается краткая характеристика принципов построения параллельных вычислительных систем, рассматриваются математические модели параллельных алгоритмов и программ для анализа эффективности параллельных вычислений, приводятся примеры конкретных параллельных методов для решения типовых задач вычислительной математики.
По сравнению с первым изданием в пособии значительно расширены материалы по кластерным вычислительным системам, анализу трудоемкости коммуникационных операций, параллельным методам решения типовых задач вычислительной математики. В пособие включены результаты вычислительных экспериментов на кластере Нижегородского университета.
Учебное пособие предназначено для широкого круга студентов, аспирантов и специалистов, желающих изучить и практически использовать параллельные компьютерные системы для решения вычислительно трудоемких задач.
Авторы
|
Роман Григорьевич Стронгин – ректор Нижегородского государственного Университета им. Н.И.Лобачевского (http://www.unn.ru). На данный момент он также возглавляет кафедру математического обеспечения ЭВМ факультета ВМК. Р.Г. Стронгин является заслуженным учёным Российской Федерации, членом редакционной коллегии журнала "Global Optimization" (1991-1998) и международного теоретического журнала "Математика" (1998-~). Р.Г. Стронгин – главный редактор серии публикаций Нижегородского Университета по математическому моделированию и оптимальному управлению, постоянный член Российской Академии Естественных Наук. Его исследовательские интересы в настоящий момент – теория и практика принятия решений. Р.Г. Стронгин – автор новых параллельных методов для решения задач глобальной оптимизации. Им опубликованы три монографии и более 270 статей в журналах "Global Optimization", "Parallel Computing", "Optimization", "Stochastics and Stochastics Reports", "Pattern Recognition and Image Analysis", "Engineering Cybernetics", "Lecture Notes in Economics and Mathematical Systems", "Журнал вычислительной математики и математической физики", "Кибернетика" и др. |
|
|
Виктор Павлович Гергель – профессор кафедры математического обеспечения ЭВМ факультета ВМК (http://www.software.unn.ac.ru/mo_evm) в Нижегородского государственного Университета им. Н.И.Лобачевского. Он возглавляет Центр компьютерного моделирования и Отделение дополнительного компьютерного обучения. Его исследовательские интересы в настоящий момент – теория и применение параллельный вычислений и разработка методов и программных систем принятия решений. В.П. Гергель – автор новых параллельных методов для решения задач глобальной оптимизации. Им опубликованы три книги и более 120 статей в журналах "Global Optimization", "Optimization", "European Journal of Operation Research", "Pattern Recognition and Image Analysis", "Engineering Cybernetics", "Журнал вычислительной математики и математической физики" и др. |
В общем плане под параллельными вычислениями понимаются процессы обработки данных, в которых одновременно могут выполняться нескольких машинных операций. Достижение параллелизма возможно только при выполнимости следующих требований к архитектурным принципам построения вычислительной системы:
Дополнительной формой обеспечения параллелизма может служить конвейерная реализация обрабатывающих устройств, при которой выполнение операций в устройствах представляется в виде исполнения последовательности составляющих операцию подкоманд; как результат, при вычислениях на таких устройствах могут находиться на разных стадиях обработки одновременно несколько различных элементов данных.
Возможные пути достижения параллелизма детально рассматриваются в [22, 29]; в этой же работе рассматривается история развития параллельных вычислений и приводятся примеры конкретных параллельных ЭВМ (см. также [9, 29, 31]).
При рассмотрении проблемы организации параллельных вычислений следует различать следующие возможные режимы выполнения независимых частей программы:
В рамках данного пособия основное внимание будет уделяться второму типу организации параллелизма, реализуемому на многопроцессорных вычислительных системах.
Одним из наиболее распространенных способов классификации ЭВМ является систематика Флинна (Flynn), в рамках которой основное внимание при анализе архитектуры вычислительных систем уделяется способам взаимодействия последовательностей (потоков) выполняемых команд и обрабатываемых данных. В результате такого подхода различают следующие основные типы систем [9, 22, 29, 31]:
Следует отметить, что хотя систематика Флинна широко используется при конкретизации типов компьютерных систем, такая классификация приводит к тому, что практически все виды параллельных систем (несмотря на их существенную разнородность) относятся к одной группе MIMD. Как результат, многими исследователями предпринимались неоднократные попытки детализации систематики Флинна. Так, например, для класса MIMD предложена практически общепризнанная структурная схема [29, 31], в которой дальнейшее разделение типов многопроцессорных систем основывается на используемых способах организации оперативной памяти в этих системах (см. рис. 1.1). Данный поход позволяет различать два важных типа многопроцессорных систем - multiprocessors (мультипроцессоры или системы с общей разделяемой памятью) и multicomputers (мультикомпьютеры или системы с распределенной памятью).

Рисунок 1.1. — Структура класса многопроцессорных вычислительных систем
Далее для мультипроцессоров учитывается способ построения общей памяти. Возможный подход — использование единой (централизованной) общей памяти. Такой подход обеспечивает однородный доступ к памяти (uniform memory access or UMA) и служит основой для построения векторных суперкомпьютеров (parallel vector processor, PVP) и симметричных мультипроцессоров (symmetric multiprocessor or SMP). Среди примеров первой группы суперкомпьютер Cray T90, ко второй группе относятся IBM eServer p690, Sun Fire E15K, HP Superdome, SGI Origin 300 и др.
Общий доступ к данным может быть обеспечен и при физически распределенной памяти (при этом, естественно, длительность доступа уже не будет одинаковой для всех элементов памяти). Такой подход именуется как неоднородный доступ к памяти (non-uniform memory access or NUMA). Среди систем с таким типом памяти выделяют:
Мультикомпьютеры (системы с распределенной памятью) уже не обеспечивают общий доступ ко всей имеющейся в системах памяти (no-remote memory access or NORMA). Данный подход используется при построении двух важных типов многопроцессорных вычислительных систем - массивно-параллельных систем (massively parallel processor or MPP) и кластеров (clusters). Среди представителей первого типа систем - IBM RS/6000 SP2, Intel PARAGON/ASCI Red, транспьютерные системы Parsytec и др.; примерами кластеров являются, например, системы AC3 Velocity и NCSA/NT Supercluster.
Следует отметить чрезвычайно быстрое развитие кластерного типа многопроцессорных вычислительных систем - современное состояние данного подхода отражено, например, в обзоре, подготовленном под редакцией Barker (2000). Под кластером обычно понимается (см., например, Xu and Hwang (1998), Pfister (1998)) множество отдельных компьютеров, объединенных в сеть, для которых при помощи специальных аппаратно-программных средств обеспечивается возможность унифицированного управления (single system image), надежного функционирования (availability) и эффективного использования (performance). Кластеры могут быть образованы на базе уже существующих у потребителей отдельных компьютеров либо же сконструированы из типовых компьютерных элементов, что обычно не требует значительных финансовых затрат. Применение кластеров может также в некоторой степени снизить проблемы, связанные с разработкой параллельных алгоритмов и программ, поскольку повышение вычислительной мощности отдельных процессоров позволяет строить кластеры из сравнительно небольшого количества (несколько десятков) отдельных компьютеров (lowly parallel processing). Это приводит к тому, что для параллельного выполнения в алгоритмах решения вычислительных задач достаточно выделять только крупные независимые части расчетов (coarse granularity), что, в свою очередь, снижает сложность построения параллельных методов вычислений и уменьшает потоки передаваемых данных между компьютерами кластера. Вместе с этим следует отметить, что организации взаимодействия вычислительных узлов кластера при помощи передачи сообщений обычно приводит к значительным временным задержкам, что накладывает дополнительные ограничения на тип разрабатываемых параллельных алгоритмов и программ.
В завершении обсуждаемой темы можно отметить, что существуют и другие способы классификации вычислительных систем (достаточно полный обзор подходов представлен в [22], см. также материалы сайта http://www.parallel.ru/computers/taxonomy/); при рассмотрении данной темы параллельных вычислений рекомендуется обратить внимание на способ структурной нотации для описания архитектуры ЭВМ, позволяющий с высокой степенью точности описать многие характерные особенности компьютерных систем.
При организации параллельных вычислений в МВС для организации взаимодействия, синхронизации и взаимоисключения параллельно выполняемых процессов используется передача данных между процессорами вычислительной среды. Временные задержки при передаче данных по линиям связи могут оказаться существенными (по сравнению с быстродействием процессоров) и, как результат, коммуникационная трудоемкость алгоритма оказывает существенное влияние на выбор параллельных способов решения задач.
Структура линий коммутации между процессорами вычислительной системы (топология сети передачи данных) определяется, как правило, с учетом возможностей эффективной технической реализации; немаловажную роль при выборе структуры сети играет и анализ интенсивности информационных потоков при параллельном решении наиболее распространенных вычислительных задач. К числу типовых топологий обычно относят следующие схемы коммуникации процессоров (см. рис. 1.1):
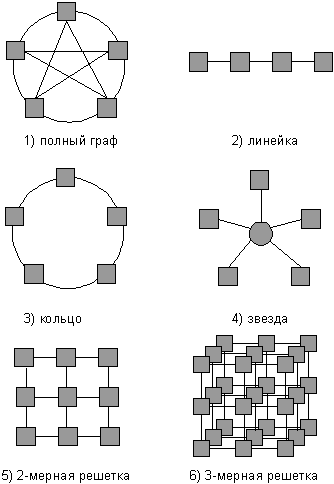
Рисунок 1.2. — Примеры топологий многопроцессорных вычислительных систем
Дополнительная информация по топологиям МВС может быть получена, например, в [9, 22 - 23, 29, 31]; при рассмотрении вопроса следует учесть, что схема линий передачи данных может реализовываться на аппаратном уровне, а может быть обеспечена на основе имеющейся физической топологии при помощи соответствующего программного обеспечения. Введение виртуальных (программно-реализуемых) топологий способствует мобильности разрабатываемых параллельных программ и снижает затраты на программирование.
Для проведения вычислительных экспериментов использовался вычислительный кластер Нижегородского университета, оборудование для которого было передано в рамках Академической программы Интел в 2001 г. В состав кластера входит (см. рис. 1.3):
Следует отметить, что в результате передачи подобного оборудования Нижегородский госуниверситет оказался первым вузом в Восточной Европе, оснащенным ПК на базе новейшего процессора INTEL® PENTIUM® 4. Подобное достижение является дополнительным подтверждением складывающегося плодотворного сотрудничества ННГУ и корпорации Интел.
Важной отличительной особенностью кластера является его неоднородность (гетерогенность). В состав кластера входят рабочие места, оснащенные новейшими процессорами Intel Pentium 4 и соединенные относительно медленной сетью (100 Мбит), а также вычислительные 2- и 4- процессорные сервера, обмен данными между которыми выполняется при помощи быстрых каналов передачи данных (1000 Мбит). В результате кластер может использоваться не только для решения сложных вычислительно-трудоемких задач, но также и для проведения различных экспериментов по исследованию многопроцессорных кластерных систем и параллельных методов решения научно-технических задач.
В качестве системной платформы для построения кластера выбраны современные операционные системы семейства Microsoft Windows (для проведения отдельных экспериментов имеется возможность использования ОС Unix). Выбор такого решения определяется рядом причин, в числе которых основными являются следующие моменты:

Рисунок 1.3. — Структура вычислительного кластера Нижегородского университета
(Нажмите на изображение для его увеличения)
В результате принятых решений программное обеспечение кластера является следующим:
Содержание
1. Принципы построения параллельных вычислительных систем
1.1. Пути достижения параллелизма
1.2. Классификация вычислительных систем
1.3. Характеристика типовых схем коммуникации в многопроцессорных вычислительных системах
1.4. Высокопроизводительный вычислительный кластер ННГУ
2. Моделирование и анализ параллельных вычислений
2.1. Модель вычислений в виде графа "операции-операнды"
2.2. Описание схемы параллельного исполнения алгоритма
2.3. Определение времени выполнения параллельного алгоритма
2.4. Показатели эффективности параллельного алгоритма
3. Оценка коммуникационной трудоемкости параллельных алгоритмов
3.1. Характеристики топологии сети передачи данных
3.2. Общая характеристика механизмов передачи данных
3.3. Анализ трудоемкости основных операций передачи данных
Передача данных между двумя процессорами сети
Передача данных от одного процессора всем остальным процессорам сети
Передача данных от всех процессоров всем процессорам
Обобщенная передача данных от одного процессора всем остальным процессорам сети
Обобщенная передача данных от всех процессоров всем процессорам сети
3.4. Методы логического представления топологии коммуникационной среды
Представление кольцевой топологии в виде гиперкуба
Отображение топологии решетки на гиперкуб
3.5. Оценка трудоемкости операций передачи данных для кластерных систем
4. Параллельные численные алгоритмы для решения типовых задач вычислительной математики
4.1. Вычисление частных сумм последовательности числовых значений
Последовательный алгоритм суммирования
Модифицированная каскадная схема
4. 2. Умножение матрицы на вектор
Достижение максимально возможного быстродействия
Использование параллелизма среднего уровня
Организация параллельных вычислений при p = n
Использование ограниченного набора процессоров
Макрооперационный анализ алгоритмов решения задач
Организация параллелизма на основе разделения данных
Параллельное обобщение базовой операции сортировки
Нахождение минимально охватывающего дерева
5. Модели функционирования параллельных программ
5.3. Организация программ как системы процессов
5.4. Взаимодействие и взаимоисключение процессов
5.5. Модель программы в виде дискретной системы
Определение состояния программы
Описание возможных изменений программы
Обнаружение и исключение тупиков
5.6. Модель программы в виде сети Петри
6. Учебно-практическая задача: Решение дифференциальных уравнений в частных производных
6.1. Последовательные методы решения задачи Дирихле
6.2. Организация параллельных вычислений для систем с общей памятью
Использование OpenMP для организации параллелизма
Проблема синхронизации параллельных вычислений
Возможность неоднозначности вычислений в параллельных программах
Исключение неоднозначности вычислений
Волновые схемы параллельных вычислений
Балансировка вычислительной нагрузки процессоров
6.3. Организация параллельных вычислений для систем с распределенной памятью
Обмен информацией между процессорами
Коллективные операции обмена информацией
Блочная схема разделения данных
© Гергель В.П., Стронгин Р.Г., 2003