Физическое проектирование оптимизации использующей эволюционные алгоритмы

I. Hameem Shanavas and R. K. Gnanamurthy, Member IACSIT

         Аннотация – Минимизация длины проводника играет важную роль в автоматизации физической разработки сверхбольших интегральных схем (СБИС = VLSI). Цель минимизации может быть достигнута путем нахождения оптимального решения для физической разработки компонентов СБИС, таких как секционирование и планирование площади. В секционировании СБИС проблема лежит в получении минимальной задержки. Также острой проблемой является минимизация кремниевой площади.

         Уменьшение минимальной задержки при секционировании и планировании площади помогает свести к минимуму длину проводника. Усовершенствование секционирования имеет влияние и на другие критерии СБИС, такие как: мощность, стоимость, тактовая частота и др. Меметичные Алгоритмы (МА) являются эволюционными алгоритмами, которые включают в себя одну или более локальных фаз поиска в пределах своего эволюционного цикла, для получения минимальной длины проводника, при сокращении задержки и секционировании площади. МА применяет своего рода локальный поиск для оптимизации секций и планирования площади СБИС.

         Алгоритм комбинирует иерархическую структуру Генетического Алгоритма (ГА) и конструктивную технику Алгоритма Имитации Отжига (АИО), для локального поиска решения секционирования и планирования площади СБИС. МА могут быстро создавать оптимальные решения для популярного бенчмарка.

 

         Основные понятия—ПРОБЛЕМА СЕКЦИОНИРОВАНИЯ, ПЛАНИРОВАНИЕ ПЛОЩАДИ, ПРОБЛЕМА.

 

I.                  ВСТУПЛЕНИЕ

         Секционирование и Планирование площади (PF) являются активными областями исследований уже, по крайней мере, четверть века. Основной причиной этого разбиения стала центральная и критическая задача. Сегодня из-за огромного увеличения системы, возникла сложность в прошлом, и ожидаемых дальнейших достижениях в микроэлектронных системах проектирования и изготовления. Широко применяются мощные инструментальные средства высокого уровня синтеза, позволяющие дизайнерам автоматически генерировать огромные системы, просто изменив несколько строк кода в функциональной спецификации. Синтез и инструменты моделирования, часто не могут справиться со сложностью всей системы в стадии разработки и также дизайнеры хотят  сконцентрироваться на важных частях системы для ускорения цикла проектирования.

         Таким образом, современное состояние технологии конструирования часто требует разбиения системы с быстрой и эффективной оптимизацией. Кроме того, технология изготовления СБИС позволяет делать все меньше и меньше размеры схемы для размещения нескольких миллионов транзисторов. Однако размер цепей ограничен в количестве внешних соединений. Такая технология изготовления требует разбиения системы на компоненты, организовав блоки не тратя бесценное пространство. Прямая реализация крупных цепей занимает большую площадь. Таким образом, большой контур должен быть разделен на небольшие подгруппы цепи. Это сведет к минимуму площадь и сложность схемы. Когда СБИС разделены, соединение между двумя модулями становится минимальным (из-за раздела сети). Такое разделение сокращает размер и, следовательно, это играет важную роль в секционировании. Это задание на проектирование с применением алгоритмических методов для решения трудных и сложных комбинаторных оптимизационных задач, как разбитие большей системы на составные части [1].

         Процесс определения формы блока и положения, с целью минимизации области называют – Планированием Площади (Floorplanning). Общая стратегия Floorplanning блоков заключается в определении, на первом этапе, а затем расположение блоков друг с другом, на основе стоимости соединительных критериев. На втором этапе, выполняется калибровка блока, с целью мнимизации общей площади чипа и завершения расположения каждого блока [2]. Когда секционирование и планирование площади объединяются (PF), такие критерии как мощность, стоимость и тактовая частота каждого блока, являются новой подцелью оптимизации. Основная же цель – оптимизация длины проводника, которая может быть достигнута путем введения Меметических Алгоритмов (Memetic Algorithm (MA)) в оба раздела PF, т.е. секционирование и планирование площади [3] и [4].

         На ранних стадиях применяется множество методов, в результате которых получено локально-оптимальное решение. Позже вводятся некоторые математические методы. Также используется некоторая эвристика, в результате чего получаемый результат – лучший, но всё же имеет свои преимущества и недостатки.

_________________________________________________________________

Manuscript received April 20, 2012; revised May 16, 2012.

I. H. Shanavas is with M.V.J College of Engineering, Bangalore - 560067,

India and Research Scholar, Anna University, Coimbatore, India (e-mail:hameemshan@gmail.com)

R. K. Gnanamurthy is Professor, Vivekanandha College of Engineering for Women, Trichengode-637205,

India and Research Supervisor, Anna University, Coimbatore, India. (e-mail:rkgnanam@yahoo.co.in)

 

Может быть много решений этой проблемы, поэтому стохастическая оптимизация еще используется, наряду с многими другими методами, как например, Алгоритм Имитации Отжига (Simulated Annealing Algorithm (SA)) который сочетает в себе Алгоритм Локального Поиска и Алгоритм Метрополиса–Гастингса.

         SA является простым алгоритмом и не требует много затрат памяти, но занимает много времени, чтобы достичь желаемого результата. Kernighan и Lin [5] предложили двусторонний график разбиения алгоритма, который стал основой для большинства последующих алгоритмов секционирования. Модифицированный Fiduccia и Mattheyses [6] алгоритм K-L стал более эффективным, предлагая перемещение одной ячейки за раз и разработку новой отдельной структуры данных. Как вид глобальной оптимизации техники, Генетический Алгоритм (GA) заменяет понятие популяции из биологии, для использования его в архитектуре таких проблем как секционирование и планирование площади схем и т.д. Этот метод применяется к ряду проблем, большинство из которых графически зависимые, потому что генетическая метафора с легкостью может быть применима к такого рода проблемам. GA более ресурсозатратный, но занимает меньше времени, нежели SA. Многие исследователи предлагали свои теории для разделения цели ГА. Работа [8] предлагаемого аппаратно генетического алгоритма по изменению ГА и локального процессора поиска, который использует расширенный объем памяти направлена на преодоление проблем местного максимума/минимума. Авторы работы [8] выразили вероятность выбора хромосомы, как функцию двух – худшей и лучшей хромосом, предложив [4] различные стоимости функции для достижения нескольких целей: минимизации задержки, сокращение площади и энергопотребления (мощности). В работе [9] авторы предложили два ГА основанных на 0-1 кодировке и другие методы на основе целочисленного кодирования. Работа, проделанная в [10] разработана на адаптивной стратегии для секционирования схем, в которых численность популяции, коэффициент кроссинговера и мутации изменяемы во время выполнения, в целях повышения производительности. Такие улучшения как оператор кроссинговера, оператор мутации или выбор различных фитнес-функций, предназначены для достижения оптимальных решений. Это означает, что теория ГА по-прежнему дает возможность новых изобретений, которые могут помочь в решении новых проблем архитектурного проектирования. Данный материал предлагает меметический алгоритм разбиения графа и проблемы планирования площади. Алгоритм включает в себя несколько особенностей генетического алгоритма, а именно – выбор популяции и кроссовер выбранных хромосом, чтобы получить наиболее устойчивое решение. Алгоритм начинается с включения схемы, как невзвешенного связанного графа, в котором каждая вершина представляет взаимосвязь между двумя входами и ребрами, после применения метафоры ГА, чтобы сгенерировать секцию, которая связана, но отключена от других подсекций,  при попытках минимизировать количество разрезов и затраченное время. Эта работа направлена на попытку совместить два алгоритма – GA и SA, с целью сокращения недостатков друг друга. Алгоритмы такого типа называются Меметическими. В этой работе рассматривается проблема секционирования СБИС с целью сокращения задержки, а также планирования площади , с целью её снижения, чтобы минимизировать длину проводника.

 

II.               СЕКЦИОНИРОВАНИЕ

         Лучшее секционирование схемы, уменьшит связь между подсхемами, что в результате даст лучшую маршрутизацию. Задача состоит в том, что проблема секционирования схемы принадлежит к классу известных NP-сложных оптимизационных проблем [11]. Эту проблему можно рассматривать как график проблемы секционирования, где каждая секция (вход и т.п.) приняты в качестве вершин и связей между ними, представляющих ребра между узлами [12], [13].

         Для запуска алгоритма, n входов размещены на графе как n вершин, и начальная популяция выбрана в качестве различных перестановок вершин данного графа. Задача сводится к связи каждой из хромосом с другой хромосомой секции графа. Предложенный алгоритм, основанный на генетическом алгоритме, может быть использован для секционирования числа узлов. Учитывая невзвешенно связанные граф G = (V, E) на множестве вершин V и ребер E. Пусть k>=2 целое число, найдем секции V1, V2, V3……………..Vk набора вершин V, таких что:

·        Графы Gi = (Vi, Ei), для всех значений i = 1, 2, 3, … k связаны.

·        Следующие значения сведены к минимуму min {|V1|, |V2|,|V3|…………. |Vk|}.

         Эти k-связные задачи являются частными экземплярами графа проблемы секционирования [15]. Поскольку точных и приближенных алгоритмов, которые работают за полиномиальное время, вобщем-то не существует, для разделения графов необходимо решить проблему с помощью эвристических алгоритмов. Генетический алгоритм это эвристическая техника, которая стремится имитировать поведение биологической репродукции и их способностей коллективно решать проблемы. ГА начинается с нескольких альтернативных решений задачи оптимизации, которые рассматриваются как особи популяции. Эти решения кодируются как двоичные строки, называемые хромосомами. Начальная популяция построена в случайном порядке. Эти индивиды оцениваются с помощью разбиения по специфической фитнес-функции. Затем ГА использует эти индивиды для воспроизведения новой популяции, в надежде на лучшие решения. В каждом поколении, две хромосомы вероятностно выбраны как родители, с вероятностью выбора пропорциональной их пригодности. Кроссовер выполняется между этими хромосомами, для создания двух новых особей, называемых потомством, путем замены частей их структуры. Таким образом, каждое потомство наследует комбинации признаков от обоих родителей. Следующий шаг – мутация. Постепенные изменения, внесенные в каждую хромосому популяции, с малой вероятностью. Это гарантирует, что ГА может изучить новые функции, которые больше не могут быть в популяции. Это делает все пространство поиска достижимым, несмотря на конечный размер популяции. Главную основу алгоритма для представления каждой вершины графа составляют места, которые могут представлять собой логический вход и соединение, представленное гранью [16][17].

 

III.             ПЛАНИРОВАНИЕ ПЛОЩАДИ

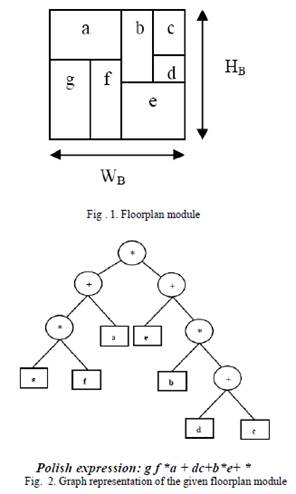
         Секция B представляет собой прямоугольник высотой НВ, шириной WB, и площадью AB. Супер-секция состоит из нескольких секций, также называемых под-площадями.  Планирование площади для n секций состоит в обходе прямоугольника R подразделенного на горизонтальные и вертикальные линии на n непересекающихся прямоугольников, каждый из которых должен быть достаточно большим, чтобы поместить секцию, вложенную в него. Данную проблему ограничивает множество жестких секций. Секции внутри данного контура имеют свободу передвижения. Допустимая упаковка в первом квадранте такова, что все модули внутри контура не должны дублироваться или накладываться друг на друга. Задачей является построение площади R такой, что общая площадь сведена к минимуму и одновременно удовлетворяет ограничениям планирования площади. Получим набор секций для указанного количества кластеров удовлетворяющих описанным ранее параметрам. Для решения этой проблемы общего планирования площади, сначала построим сетевой граф (см. рисунок 1 и 2), а затем пройдем заданный алгоритм, чтобы получить решение. Граф состоит из двух видов вершин, горизонтальных и вертикальных. Сетевой граф G=(V,E) также построен. ‘*’ – представляет вертикальные разрезы блоков, ’+’ – горизонтальные.