Алгоритм автоматической регистрации, сегментации и моделирования медицинских изображений
Авторы: V. Petrovic, T. Cootes, C. Twining, C. Taylor
Перевод: Плахова Е.Е.
Источник (интернет-ресурс):
http://personalpages.manchester.ac.uk/staff/timothy.f.cootes/Papers/MIUA06/petrovic_miua06.pdf
Аннотация
Описана структура алгоритма, который одновременно сегментирует и регистрирует набор медицинских изображений в автоматическом режиме, последовательно строя модель деформации структуры и формы набора. Такая структура расширяет существующие групповые подходы к регистрации и моделированию путем явного моделирования в каждом вокселе всех типов ткани отдельно вместо ожидаемой интенсивности. Это уменьшает влияние на модель недостатков алгоритма отображения, и, таким образом, метода визуализации. При определении оптимального деформационного поля изображений в наборе каждый его следующий элемент генерируется из модели сегмента фракций и текущей оценки его распределения интенсивности для каждого типа ткани (т.е. оценки того, как модель будет проявляться с учетом условий формирования изображения). Также представлен метод определения оптимального числа типов тканей и полной автоматизации подхода как методы построения модели, обеспечивающие эффективное приближение. Детально описан алгоритм и представлены результаты его применения на наборе МРТ изображений головного мозга.
Описана структура системы, которая одновременно сегментирует и регистрирует набор медицинских изображений в автоматическом режиме путем пошагового построения модели структуры и формы набора деформаций. Структура детализирует существующую классификацию благодаря явному моделированию фрагментов ткани каждого типа в каждом снимке и дает лучшие результаты, чем построение модели вероятностей яркости каждого изображения.
Введение
Данная статья предлагает полностью автоматизированный подход анализа, распознавания и представления структуры набора медицинских изображений. В идеале, имея набор изображений различной структуры, хотелось бы получить эффективным и надежным методом:
- набор полей деформации, определяющих тесные соответствия между изображениями (регистрация);
- классификацию вокселей каждого изображений набора по различным типам тканей (сегментация);
- статистическое отображение изменения формы и внешнего вида по всему набору изображений (моделирование).
В настоящее время существуют значительные научные исследования, которые могут обеспечить каждое из данных требований в отдельности. Нежесткие методы регистрации изображений позволяют получить плотность и пространственные связи между элементами набора [1-3], сегментация головного мозга на МРТ изображениях описана в [4,5], в то время как Статистические Видовые Модели [1] распознают и описывают изменение вида (формы и текстуры) моделируемой структуры.
Различными методами также предложено комбинирование техник попарно, к примеру, сегментация и регистрация активными контурами [6], а также апостериорный максимум с использованием скрытых марковских сетей и B-сплайновая нежесткая регистрация [7]. Модели деформации строятся по связям, оцененным методом нежесткой регистрации, но также доказано, что интеграция моделирования и регистрации дает более точный результат моделирования, чем параллельное их выполнение [1,10].
В данной статье описан алгоритм, который комбинирует сегментацию, регистрацию и моделирование в простом итеративном фреймворке, который последовательно улучшает структурный анализ с целью удовлетворения всех изложенных выше требований. Метод описан в деталях в разделе 2, в то время как результаты его применения на наборе снимков МРТ головного мозга представлены в разделе 3.
Общий вид алгоритма представлен на рисунке 1. Имеется набор из N снимков Ti, i=1…N, (обучающее множество), предполагается, что его элементы приведены к практически одинаковому виду (либо благодаря протоколу визуализации, либо, к примеру, путем аффинной регистрации одного элемента с использованием взаимной информации). Далее предполагается, что структурно изображения состоят из M отдельных типов тканей, которые имеют значения функции плотности вероятности Θi. Далее, Wi() задает пространственную деформацию связи между системой отсчета и изображением Ti. Сегментация, регистрация и моделирование выполняется по следующим этапам (см. ниже для более подробной информации):

Рисунок 1 - Общий вид алгоритма
- Перестроить каждое обучающее изображение Ti в системе отсчета, используя текущую оценку деформационного поля. Ti'=Wi-1 (Ti).
- Вычислить гистограмму интенсивностей Ti'; определить, подходит ли смешанная модель для оценки распределения и пропорций каждого чистого типа ткани (средние значения, СКО и веса закодированы в Θi={µij,σij,ωik}). Использовать полученные распределения для оценки наиболее вероятной доли каждой ткани в каждом вокселе, закодированных в наборе изображений долей тканей Fi(j), j=1…M для каждого обучающего экземпляра.
- Объединить все изображения долей тканей с соответствующими экземплярами обучающего набора для построения модели, {F(1)…F(M)}.
- Перестроить каждое изображение из набора обучения с использованием текущей оценки среднего распределений чистых типов тканей, µij, и текущей модели долей ткани, Si=∑j=1MµijF(j).
- Найти оптимальное число классов тканей М путем оценки Описательной Длины (ОД) моделируемого обучающего набора в виде функции М, см. [1], и используя тот, что приводит к минимальной ОД (МОД).
- Заменить текущую оценку Wi лучшей зарегистированной на наборе Ti Si, минимизируя таким образом меру сходства Dim(Ti,Wi(Si).
Во время первого прохода алгоритма применяются шаги 1 и 2 для всех изображений, а затем объединяем их (шаг 3) в исходной модели ткани фракций на каждом вокселе в системе отсчета. Затем многократно повторяем шаги 2-5, пока не будет найден оптимальный M. Затем применяем шаги с 1-6 к каждому изображению несколько раз, выполняя регистрацию грубых деталей на ранних стадиях и постепенно по мере увеличения итерации уменьшая их долю. Процесс построения модели формы исключен из рис.1 ради ясности, но является неотъемлемой частью шага 3, и может быть также использован для ограничения оптимизации поля деформации на шаге 6 [10].
2.1 Сегментация
Если следовать Pokric ET A1. [4], можно считать, что объекты в МРТ головного мозга построены из небольшого числа (M) различных типов тканей и что каждый воксель содержит либо чистую ткань, либо смесь более двух различных тканей (смешанные объемы). Если известно распределение интенсивности для этих классов, можно построить свертку конкретного дробного распределения. В экспериментах, описанных в дальнейшем, предполагается, что распределение чистой ткани является нормальным, pi(g)=N(g : µi,σi2), тогда распределение для частичного объема фракции f для типа ткани i и 1-f для типа j имеет вид:
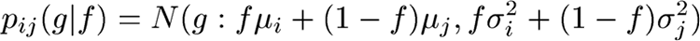 |
(1) |
Распределение всех смешанных объемов, содержащих i и j, вычисляется по (2), при этом предполагается, что все значения f содержатся в интервале [0, 1] с вероятностью (p(f)=1).
 |
(2) |
Если предположить, что любой воксель содержит не более 2 различных типов тканей, то нужно рассматривать только чистую M классов ткани с распределениями pk(g),k=1…M, и M(M-1)/2 смешанных классов ткани (перечисленные pk (g),k=(M+1)…Mt=M(M+1)/2) . Таким образом, измеренное распределение интенсивности изображения, H(g), можно приблизить как взвешенную сумму &Theta={µi,σi,ωk})(i=1..M, k=1..Mt):

Рисунок 2 - Кумулятивная функция D от итерации для простых средних (сплошная), наполовину усеченных средних (пунктир) и средней оценки модели (пунктирная линия)
Таким образом, можно выполнить оптимизацию для оценки параметров θ, которые оптимизируют Dp(p(g:θ),h(g)), где Dp(p,g) является подходящей мерой расхождения между распределениями. Вероятность того, что воксел с интенсивностью g относится к классу k задается Pk(g)=wkpk(g)/(∑wkpk(g) (см. рис. 4). Этот воксель может быть отнесен к классу kc=arg maxkPk(g). Однако, в действительности мы заинтересованы в оценке доли каждого класса чистой ткани (fi,i=1..M) в вокселе, а не в вероятности каждого класса. Если kc≤M, то воксель является чистой тканью, поэтому определяем fkc=1 и fi≠kc=0. Если kcM, то воксель классифицируется как смешанный объем, содержащий два типа, скажем, тип I и тип j. В этом случае необходимо найти наиболее вероятное значение фракции для каждого типа ткани. Определяем:
 |
(4) |
где pij(g|f) определен выше в уравнении (1). Затем устанавливаем fj=1- fj и fk≠i,j=0. На рис. 4 4 показан пример этого, демонстрирующий что вероятность ткани не совпадает с оценками чистых фракций ткани. Используя этот подход, вычислим М изображений, {F(1)…F(M)}, записывая долю каждого типа ткани для каждого вокселя в нормализованную версию изображения i (которая проецируется в системе отсчета).
2.2 Построение модели
Получили модель из M дробных изображений от каждого из N изображений. На построение модели могут быть наложены ограничения, а именно - ограничить все воксели к смеси не более двух типов ткани, но хотя это способствует приближению, обнаружили, что даже простое среднее является достаточно сильным для управления процессом приближения.
 |
(5) |
Большая скорость сходимости достигается за счет использования более надежной оценки усеченное среднее (оцениваются выбросы). На отдельном наборе данных из 50 синтетических, наполовину светлых, наполовину темных изображений, которые меняются случайным образом в переходной позиции интенсивности и уровней, обнаружено, что использование только половины образцов в средней оценке значительно улучшает скорость регистрации конвергенции. Конвергенция для такого набора данных показана как кумулятивная функция (D) от итерации для простых средних), наполовину усеченных средних и средней оценки модели на рис. 2.
2.3 Реконструкция изображения
В целях приведения обучающего набора деформационное поле является оптимальным между T(i) и моделью, воплощенной в реконструкции, S(i), полученной с использованием модели фракций тканей и оценки распределения интенсивности для каждого типа ткани в текущем изображении (т.е.оценки того, как модель будет появляться с учетом условий формирования такого изображения). Чистый типы тканей, обладающий нормальным распределением, оптимально представлен их средними значениями m(j), в то время как смешанные объемы вокселей представлены суммами средних чистых типов, взвешенных текущими долями этих же типов:
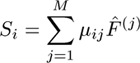 |
(6) |
Для примера, см. рис. 5. В идеале S(i) является зашумленной версией T(i) - но на практике она становится нечеткой из-за перекосов и постепенно становится острее и ближе к T(i) - как выравнивание и улучшение модели. Параметры деформации w(i) оптимизированы. Что касается целевой функции измерения сходства между Т(i) и S(i) в рамках обучающих изображений - Dim(Ti,Wi-1(Si)). Деформация оптимизирована в несколько этапов и на нескольких уровнях разрешения (ради эффективности) путем перемещения отдельной контрольной точки или их группы по сцене, см. [10] для деталей.
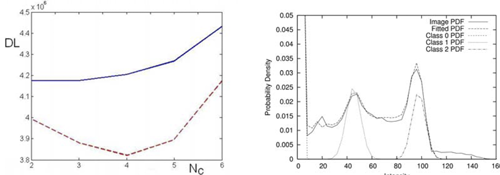
Рисунок 3 - График зависимости длины моделируемого обучающего множества от числа классов (слева), а также распределение интенсивности для изображений на рис. 4 и результирующего соотношения чистой и частичной ткани класса
2.4. Число классов сегментации
Чтобы автоматически инициализировать анализ изображения и избежать явного предварительного предположения о его структуре ищем оптимальное количество типов ткани M автоматически. С этой целью используем предложенный сегментационно-регистрационный алгоритм минимальной длины описания, аналогично [1]. Начнем с минимальным М = 2 и выполним шаги 2-4. Для каждого шага оцениваем длину описания переданного обучающего набора, используя результирующую модель, учитывая стоимость модели, ее параметров и остаточных изображений.
(Ri=Si-Ti), Ctotal+Cparameters+Cresiduals
На практике остаточный параметр доминирует над стоимостью и, улучшая модель и восстановленные изображения, явно улучшает длину описания. Если добавление другого класса восстановленных изображений улучшает стоимость модели, то это уменьшает длину описания. Оптимальное число классов в результате дает минимальную длину описания (МДО). Отметим, что по мере улучшения модели путем совмещения изображений, можно ожидать, что оптимальное значение М будет меняться на протяжение процесса регистрации, см. раздел 3. Подробнее о том, как оценить С, описано в [1].
3 Эксперименты и результаты
Применили метод к набору из 32 двумерных срезов МРТ головного мозга (выбрав эквивалентные срезы из обработанных аффинными преобразованиями трехмерных наборов) (рис. 4). Использовали сумму квадратов разностей между двумя изображениями, Dim(), и расхождения между распределениями их интенсивности, Dp(). На рис. 4 показано одно из изображений обучающего множества. По гистограмме распределения чистых и смешанных классов тканей (рис. 3), можно оценить для каждого вокселя вероятность принадлежности к каждому чистому классу ткани (Pi(x,y) в колонке 2) и к каждому смешанному классу (Fi(x,y) в колонке 3). В итоге, комбинируя эти дробные доли со средними значениями распределений чистых классов, можно генерировать преобразование, S(x,y).
Автоматическая оценка числа классов тканей в данных показана на рис. 3. Пока изображения не выровнены, достаточно меньшего типа классов, в этом случае М=3 является оптимальным. После преобразования (выравнивания) изображений, структуры на них становятся более когерентными и проявляются на дальнейших моделях. Рисунок 3 показывает, сто на регистрируемом наборе существует четыре разных последовательных типа тканей. Поскольку к изображению не применялось никакой «зачистки черепа», этот регион также вносится в распределение интенсивностей путем добавления к определенным на начальном этапе трем типам (белое и серое вещество и CSF+фон).
На рис.5 показаны модели средних значений долей для трех типов ткани в начале и в конце регистрации, вместе с примером результата преобразования с использованием средних значений каждого чистого класса ткани.

Рисунок 4 - Срезы МРТ головного мозга и результаты их сегментации. Колонка 2 - вероятности чистых классов, колонка 3 - оценки их долей
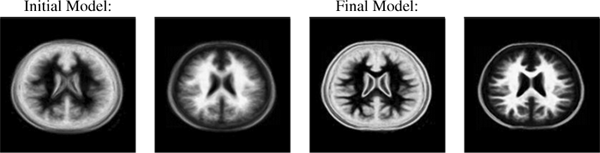
Рисунок 5 - Оценка средних значений долей классов ткани F2(x,y) и F3(x,y) в начале и в конце регистрации
4 Анализ
В работе продемонстрирована возможность объединения процессов сегментации, моделирования и регистрации в один фреймворк и выполнения комплексного анализа структуры в полностью автоматическом режиме. Построив модель сегментации долей, а не интенсивности, отделили моделирование от деталей процесса формирования изображения, и сосредоточились на явном изучении структуры тканей в медицинских изображениях. Окончательная модель включает в себя как информацию о классах ткани, так и статистические модели изменения формы. Такую модель возможно совместить с новыми изображениями, полученными при разных условиях, ожидается, что такие модели будут пользоваться широким применением.
Также расширена возможность реализации трехмерных данных (расширение естественно). Дальнейшая работа будет сконцентрирована на включении пространственных связей в оценку оптимального числа типов тканей так же, как и их интенсивностей. Дальнейшие улучшения также могут быть сделаны путем включения текущих оценок средних долей в качестве предварительного значения при сегментации каждого изображения.
Источники
- C. J. Twining, T. F. Cootes, S. Marsland et a]. “A unified information-theoretic approach to groupwise non-rigid registration and model building.” In Proceedings of Information Processing in Medical Imaging (IPMI), volume 3565 of Lecture Notes in Computer Science, pp. 1—14. Springer, 2005.
- K. K. Bhatia, J. V. Hajnal, B. K. Puri et a1. “Consistent groupwise non-rigid registration for atlas construction.” Proceedings of the IEEE Symposium on Biomedical Imaging (ISBI) pp. 908—911, 2004.
- B. Zitova & J. Flusser. “Image registration methods: A survey.” Image and Wsion Computing 21, pp. 977 — 1000, 2003.
- N. A. T. M. Pokric & A. Jackson. “The importance of partial voluming in multi-dimensional medical image segmentation.” In Proceedings of Information Processing in Medical Imaging (IPMI), volume 2208 of Lecture Notes in Computer Science, pp. 1293—1294. Springer, 2001.
- Y. Zhang, M. Brady & S. Smith. “Segmentation of brain mr images through a hidden markov random field model and the expectation-maximization algorithm.” IEEE Transactions on Medical Imaging 20, pp. 45 — 57, 2001.
- A. Yezzi, L. Zollei & T. Kapur. “A variational framework for inregrating segmentation and registration through active contours.” Medical Image Analysis 7, pp. 171—185, 2003.
- D. R. C. Xiaohua, M. Brady. “Simultaneous segmentation and registration for medical image.” In Proceedings of MICCAI 2004, number 3216 in Lecture Notes in Computer Science, pp. 663 — 670. 2004.
- A. F. Frangi, D. Rueckert, J. A. Schnabel et a1. “Automatic construction of multiple-object three-dimensional statistical shape models: Application to cardiac modelling.” IEEE Transactions on Medical Imaging 21(9), pp. 1151—1166, 2002.
- D. Rueckert, A. F. Frangi & J. A. Schnabel. “Automatic construction of 3D statistical deformation models using non-rigid registration.” Lecture Notes in Computer Science 2208, pp. 77—84, 2001.
- T. Cootes, C. Twining, V. Petrovic et a1. “Groupwise construction of appearance models using piece-Wise affine deformations.” In Proceedings of the 16th British Machine Wsion Conference (BMVC), volume 2, pp. 879—888. 2005.