Сравнительный анализ алгоритмов фильтрации медицинских изображений
Авторы: Бондина Н.Н., Калмычков А.С., Кривенцов В.Э.
Источник: Вісник Національного технічного університету "Харківський політехнічний інститут". Збірник наукових праць. Серія: Інформатика та моделювання. – Харків: НТУ "ХПІ", 2012.–№38.–с.14-25.
Аннотация
Рассмотрены алгоритмы линейной, нелинейной и адаптивной фильтрации медицинских изображений. Определены особенности поведения алгоритмов в зависимости от характера шума, параметров фильтра, размеров апертуры. Проанализированы сложность и быстродействие алгоритмов фильтрации. На основе полученных данных приведены рекомендации по использованию фильтров. Библиогр.: 12 назв.
Ключевые слова: фильтрация медицинских изображений, алгоритмы фильтрации,адаптивная фильтрация.
Постановка проблемы и анализ литературы. Медицинские исследования с помощью современных методов визуализации позволяют заглянуть внутрь объектов живого организма и диагностировать его состояние. Эта задача решается с помощью цепочки этапов обработки изображения с целью анализа и распознавания объектов. Формирование изображений в различных устройствах и их дальнейшая передача по разным каналам вносят искажения в изображения, поэтому первым этапом в обработке изображений является фильтрация изображений или устранение в них низкочастотного шума. Этот этап позволяет отличить интересующие нас объекты от всех других и от фона. Важность этого этапа объясняет объём научно-технической литературы, посвящённой методам фильтрации изображений[1–6]. Анализ публикаций показывает, что наиболее адекватным и с точки зрения использования в практических задачах являются модели аддитивного Гауссова и импульсного шума. Аддитивный Гауссов шум характеризуется добавлением к каждому пикселю изображения значений из соответствующего нормального распределения с нулевым средним значением. Такой шум появляется в устройствах формирования цифровых изображений. Импульсный шум характеризуется заменой части пикселей значениями фиксированной или случайной величины. Такой шум связан с потерями при передаче изображений по каналам связи. В реальном изображении можно встретить как аддитивный, так и импульсный шум, такой шум называют комбинированным.
Все виды фильтров можно разделить на такие классы: частотные, линейные, нелинейные, комбинированные, гибридные и адаптивные.
В классе частотных фильтров обработке подлежат коэффициенты разложения зашумленного сигнала по Фурье базису или другим базисам, в частности, вейвлет-базису. Такие алгоритмы достаточно эффективны с точки зрения удаления шума, не требуют априорной информации, которая часто отсутствует на практике. При этом необходимо выбрать параметры алгоритмов, исходя из условия минимума среднеквадратичной ошибки фильтрации [7]. Выбор этих параметров основан на знании дисперсии шума изображения. Преобразование Фурье имеет особую важность для линейных фильтров, поскольку умножение в Фурье-области для частотных методов – это операция свёртки для исходного изображения. Линейные фильтры используют именно операцию свёртки.
В цифровой обработке сигналов широко используются методы линейной фильтрации изображений, что объясняется простотой реализации и интерпретации этих методов [1–6]. Однако успешность их применения сильно зависит от вида шума и даёт хорошие результаты лишь в случае гауссова аддитивного шума [1–4]. В случае импульсного шума эффективнее работают методы нелинейной фильтрации, в частности медианные и ранговые [3–5]. В случае комбинированного шума можно последовательно применять линейные и нелинейные фильтры или компоновать эти фильтры так, чтобы усилить их сильные стороны и ослабить недостатки, это происходит при использовании гибридных фильтров [1, 11]. Противоречие по зависимости степени подавления шумов и искажения сигнала от апертуры фильтра в некоторой степени сглаживается при применении фильтров с динамическим размером маски, с адаптацией размеров апертуры под характер изображения. В адаптивных фильтрах большие апертуры используются в монотонных областях обрабатываемого сигнала (лучшее подавление шумов), а малые – вблизи неоднородностей, сохраняя их особенности[1,10,12].
Медицинские изображения, получаемые в различных устройствах, могут иметь особенности, связанные с физическими принципами, лежащими в основе визуализации. Наиболее широко распространены ультразвуковые методы визуализации внутренних органов человека. Это связано с безопасностью, с одной стороны, и высокой информативностью и достоверностью ультразвуковых исследований, с другой стороны. Компьютерная томография и магнитно-резонансная томография также позволяют визуализировать то, что недоступно непосредственному наблюдению. Проекционные данные, регистрируемые в реальных компьютерных томографических системах, носят случайных характер, обусловленный такими факторами. Во-первых, используемое рентгеновское излучение имеет ярко выраженную квантовую структуру. Число квантов, испускаемых рентгеновскими источниками за фиксированный интервал времени, является случайной величиной, поэтому элемент случайности заложен в самой природе источника излучения. Во-вторых, проходя через исследуемый объект, кванты поглощаются веществом случайным образом. В целях снижения дозы облучения, целесообразно снижать мощность излучения, что неизбежно приводит к увеличению относительного уровня шума.
Для решения проблемы восстановления изображения по проекционным данным используют алгоритмы с малой величиной систематической ошибки, а затем выполняют фильтрацию восстановленного изображения. Использование комбинированного алгоритма, представляющего собой последовательность процедур медианной фильтрации и линейной фильтрации, в данном случае не позволяет в полной мере сохранять резкиеперепады уровня изображения из-за совпадения спектров случайной ошибки восстановления и "контрастных элементов" восстанавливаемого изображения. Это приводит к искажению формы фронтов и контрастных объектов. Поэтому для фильтрации контрастных изображений используют модификацию медианного фильтра. Применение такого фильтра позволяет получить лучшую гладкость отфильтрованных данных, при этом сохраняя контрастные детали изображения. При визуализации внутренних органов ультразвуковыми методами часто возникает необходимость различать ткани с близкими эхогенными значениями, то есть слабо различимыми на изображении. Исходя из особенностей медицинских изображений, для получения хорошего результата в ходе обработки часто используют комбинацию различных алгоритмов. В любом случае необходимым и важным этапом обработки медицинских изображений является фильтрация. Знание преимуществ и недостатков различных методов фильтрации даст возможность подобрать необходимое сочетание алгоритмов для улучшения эффективности обработки изображений.
Цель статьи – сопоставление возможностей известных алгоритмов фильтрации изображений по удалению Гауссова, импульсного и комбинированного шумов, сравнение их по сложности и быстродействию для использования в обработке медицинских изображений.
Обзор и сопоставление алгоритмов фильтрации. Линейные фильтры также называют сглаживающими или усредняющими, потому что ответ линейного фильтра просто усредняет значение пикселей, содержащихся в апертуре, и таким образом сглаживает изображение. Напомним некоторые термины, применяемые при линейной фильтрации. В ходе обработки используется небольшой прямоугольный или квадратный участок изображения и на нём определяется функция. Такой участок называется апертурой или окном, а заданная на ней функция – весовой функцией или функцией окна. Апертура вместе с заданной на ней функцией называется маской. Примеры фильтров:

Если все коэффициенты фильтра равны, как в H1, то фильтр называется фильтром-ящиком [1,3]. Те пиксели, которые при обработке более важны, можно выделить, придавая им больший вес коэффициентами, как в H2, H3. При работе с фильтрами-ящиками следует иметь в виду, что их структура позволяет ускорить процесс вычислений при обработке изображения. Дело в том, что при сдвиге апертуры на один пиксель сумма, которую нужно вычислить, частично уже вычислена для предыдущей свёртки, нужно только вычесть сумму для самого левого столбца маски предыдущей свёртки и добавить сумму для самого правого столбца маски на новом шаге [3]. Перепады яркости, связанные с наличием шума, размываются и это – положительный эффект, вместе с ними размываются и перепады яркости, связанные с деталями самого изображения, что нежелательно. Требуется ослабить перепады яркости в первом случае и, по возможности, сохранить их во втором случае.
Для этого нужно подобрать размеры апертуры и специальные веса, которые позволяют воздействовать именно на шум. Пусть, например, используется маска N×N, в пределах её полезное изображение имеет постоянную яркость f, шум с независимыми значениями отсчетов nk,m, средним значением μ = 0 и дисперсией σ2 в пределах маски. Отношение квадрата яркости (i,j)-го пикселя к дисперсии шума, т.е. отношение сигнал/шум, равно f2/Σ2[4]. В результате фильтрации отношение сигнал/шум становится равным N2f2/σ2, т.е. возрастает пропорционально площади маски. Применение маски 3×3, в среднем, повышает отношение сигнала к шуму в 9 раз. Следует заметить, что увеличение размеров апертуры также приведёт к увеличению вычислительных затрат при обработке изображения. Подбор коэффициентов маски также улучшает подавление шумов. Как показано в [3], лучшие сглаживающие фильтры удовлетворяют условию, что маски фильтра должны постепенно приближаться к нулю, такой вывод получен на основе анализа поведения преобразования Фурье. В качестве примера можно привести двумерный биномиальный фильтр, составленный из вертикального и горизонтального биномиальных фильтров:

Для получения коэффициентов биномиальных фильтров с большими размерами апертур можно использовать вычислительную схему треугольника Паскаля. К тому же, для сокращения операций сложения и умножения можно, как это показано для фильтра H3, использовать попеременно вертикальную и горизонтальную маски к изображению, что для масок больших размеров значительно сократит вычислительные затраты [3].
Фильтр Гаусса также уменьшает влияние пикселей друг на друга с расстоянием. Ядро гауссовского фильтра есть:
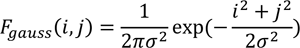
При некоторых видах шума гауссовская фильтрация позволяет размывать шум, подвергая содержательные контуры изображения размытию в меньшей степени. Например, если на изображении нужно размыть мелкие детали, не требующие отделения от фона, а крупные объекты, представляющие интерес, можно выделить в дальнейшем с помощью бинаризации. Гауссовская фильтрация используется совместно с лапласианом при подчёркивании границ. Известно, что лапласиан увеличивает шумы в изображении, совместное же использование лапласиана с гауссовской фильтрацией делает этот эффект менее значительным.
С физической точки зрения, H1, H2, H3 являются фильтрами нижних частот, подавляющими гармоники и шума, и полезного изображения, что приводит не только к ослаблению шума, но и к размыванию контуров на изображении. Это следует иметь в виду при подавлении Гауссова шума с помощью увеличения апертуры линейного фильтра или применения специальных коэффициентов маски: и то и другое увеличивает соотношение сигнал/шум в результате обработки изображения, но и размывает контуры изображения, чем ухудшает его.
Для удаления Гауссова шума наилучшим является фильтр Винера [6,9], поскольку его коэффициенты вычисляются из условия минимизации ошибок фильтрации в результате решения уравнения Винера–Хопфа. Для реализации этого алгоритма необходимо знание корреляционных функций исходного изображения. Вместо этого вычисляют спектральные плотности мощности, представляющие собой дискретное преобразование Фурье корреляционных функций. Хотя для вычислений преобразования Фурье используются быстрые алгоритмы, фильтр Винера требует дополнительных вычислительных затрат по сравнению с обработкой линейными фильтрами, поэтому на практике часто предпочитают работать с линейными фильтрами, а коэффициенты подбирать в ходе обработки.
Импульсный шум характеризуется заменой части пикселей на изображении значениями фиксированной или случайной величины. На изображении такие помехи выглядят изолированными контрастными точками, например, шум "соль и перец" содержит белые и чёрные точки, беспорядочно разбросанные по изображению. Для удаления импульсного шума используется специальный класс нелинейных фильтров, построенных на основе ранговой статистики. Идея алгоритма обработки заключается в определении позиции импульса и замене его оценочным значением, при сохранении остальных пикселей изображения неизменными. Такие фильтры относятся к нелинейным фильтрам.
В этом случае также используют маски. Но работают они по - другому, значения пикселей, соответствующих маске, записываются в ряд. После сортировки этого ряда ответ фильтра получается как центральный элемент в отсортированной последовательности, то есть медиана ряда. Так работает хорошо известный медианный фильтр. Известно, что применение медианных фильтров даёт хорошие результаты для сохранения перепадов оттенков, различных границ и устранения локальных пиков яркости на изображениях, искажённых импульсным шумом. Свойство медианных фильтров сохранять монотонные последовательности позволяет применять медианную фильтрацию для устранения аномальных значений в массивах данных, уменьшения выбросов и импульсных помех. Таким образом, по сравнению с линейными фильтрами медианные лучше сохраняют контуры изображения. Основные недостатки медианной фильтрации – менее эффективное, чем у линейных фильтров, подавление Гауссова шума и появление на изображении размытых контуров деталей вследствие ослабления исходного сигнала в результате работы медианного фильтра[7]. Медианные фильтры используют также итеративно. Хорошего качества фильтрации можно добиться, если медианный фильтр применять к изображению, пока изображение изменяется под влиянием медианного фильтра [3].
Кроме медианного фильтра можно использовать экстремальные фильтры, в этом случае вместо медианы ряда берут минимальное или максимальное значение ряда [1,3]. Такие фильтры хорошо справляются с шумом "соль и перец". Для устранения недостатков медианных фильтров алгоритмы их работы совершенствуют, учитывая особенности как изображения, так и шума [7]. Например, используют взвешенные медианные фильтры. Как и в случае линейных фильтров, некоторым пикселям придают больший вес. Это приводит к тому, что фильтр в ряду значений для последующей сортировки встречается столько раз, каков его вес и таким образом несколько повышается вероятность того, что он не будет отброшен как импульс. Взвешенный медианный фильтр:
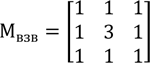
даёт лучшие результаты, чем медианный фильтр при небольшихплотностях шума [9].
Следующий вариант метода ранговой статистики – это ранжирующий фильтр и его модификация – рекурсивный ранжирующий фильтр. Для ранжирующих фильтров характерно, что ряд, подготовленный для сортировки, не включает центральный отсчет маски фильтра, и после сортировки ряда производится вычисление значения m(n). Вычисление выходного значения фильтра, которым заменяется центральный отсчет, выполняется по формуле:

где m(n)=XN/2+XN/2+1.
Значение коэффициента доверия α связывается определенной зависимостью со статистикой отсчетов в окне фильтра (например, полной дисперсией отсчетов, дисперсией разностей x(n)-xi(n) или m(n)-xi(n), дисперсией положительных и отрицательных разностей x(n)-xi(n) или m(n)-xi(n), и т.п.). По существу, значение коэффициента α должно задавать степень поврежденности центрального отсчета и, соответственно, степень заимствования для его исправления значения из отсчетов m(n). Выбор самой функции и характер зависимости от нее коэффициента α может быть достаточно многообразным и зависит как от размеров апертуры фильтра, так и от характера изображений и шумов [9]. Во многих случаях улучшение работы фильтра может быть получено, если реализовать соответствующий фильтр в рекурсивной форме (рекурсивный ранжирующий фильтр(РФ)). Для этого скользящее окно должно содержать как зашумлённые, так и уже отфильтрованные пиксели. В [9] описан классификатор, позволяющий относить просматриваемые пиксели к двум классам: повреждённые и неповреждённые пиксели, то есть управлять ходом фильтрации. Опыт показывает, что РФ имеет лучшее восстановление, чем обычный медианный фильтр.
К нелинейным фильтрам относится также двумерный фильтр Калмана. Идея работы этого фильтра заключается в использовании двумерного фильтра с таким видом импульсной характеристики, при которой его практическая реализация была бы простой, и с такими параметрами этой импульсной характеристики, при которых эффективность фильтрации приближалась бы к потенциально возможной. Создать фильтр с такими свойствами удается на основе аналогии с одномерным фильтром Калмана[6]. Рекуррентная формула работы фильтра Калмана имеет такой вид:
x´(i,j)=B•F•(x´(i-1,j)+x´(i,j-1))-(B•F)2•x´(i-1,j-1)+A•y(i,j)
где x´(i,j) – изменяемые в ходе фильтрации значения; B, F, A – коэффициенты, подлежащие определению; y(i,j) – текущее наблюдение. Подбор коэффициентов фильтра специальным образом позволяет фильтру вести себя "разумно": подавлять шумы и не увеличивать динамические ошибки фильтрации. Работа фильтра Калмана требует выполнения на каждом шаге обработки всего трех операций умножения и трех операций суммирования, причем структура алгоритма универсальна и, в частности, не зависит от отношения сигнал/шум. Для сравнения, масочный фильтр с размером окрестности 3×3 элементов требует выполнения на каждом шаге девяти умножений и восьми суммирований. Таким образом, по количеству операций рекуррентный фильтр выигрывает у простейшего масочного практически в три раза. Очевидно, что попытка улучшить качество фильтрации масочным фильтром за счет увеличения размера применяемой окрестности приводит к увеличению числа операций и дальнейшему увеличению его проигрыша по этой характеристике.
Актуальной остаётся задача разработки алгоритмов фильтрации для комбинированных шумов. Стремление использовать для этой цели положительные стороны обоих методов фильтрации – линейной и медианной приводит к комбинированным и гибридным фильтрам. В случае комбинированных фильтров к обрабатываемому изображению последовательно применяются медианный фильтр и линейный фильтр [10]. Сначала с помощью медианного фильтра устраняется импульсный шум, а затем с помощью линейного сглаживается остаточный низкоамплитудный шум. В гибридных фильтрах сначала определяются выходные значения подфильтров (в качестве под фильтров можно использовать линейные или медианные фильтры), апертуры которых некоторым образом расположены в пределах основной апертуры фильтра, а затем к набору, содержащему выходы подфильтров, применяют медианный или линейный фильтр. В первом случае в качестве выхода гибридного фильтра выбирается медиана, полученная после сортировки выходных значений линейных подфильтров, во втором – взвешиваются с определёнными весами медианы подфильтров. Гибридные методы фильтрации, совмещающие достоинства методов ранговой обработки и линейной фильтрации, позволяют снизить уровень как Гауссова шума, так и импульсных помех [11]. Гибридный фильтр превосходит медианный, поскольку позволяет уменьшить искажения контуров малоразмерных объектов. По быстродействию гибридные фильтры несколько уступают линейным и медианным, но незначительно.
Линейные и медианные фильтры не учитывают изменений статистических характеристик в самом изображении. Алгоритмы, позволяющие учитывать такие изменения, называются адаптивными. Известно несколько вариантов алгоритмов адаптивной линейной и медианной фильтрации. Простейший из таких вариантов, учитывающий изменение характеристик изображения с неизменным размером апертуры, описан в [1]. Для этого алгоритма нужно знать математическое ожидание изображения mi, дисперсию всего изображения ση2, дисперсию апертуры σi2, использовать формулу:
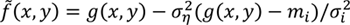
где f(x,y) – отфильтрованное изображение; g(x,y) – зашумленное изображение. Формулу, описывающую работу фильтра, можно пояснить таким образом. Если дисперсия апертуры значительно превышает дисперсию изображения, то мы находимся в области перепада в изображении, который желательно сохранить, и выход фильтра будет g(x,y). Если же две дисперсии близки по значению, то апертура имеет те же свойства, что и всё изображение, и в этом случае локальный шум может быть уменьшен с помощью усреднения (выход фильтра – mi).
Таким образом, знание дисперсий изображения и окна позволяет различать области с перепадами в изображении и области фона и соответственно адаптировать к этим особенностям поведение фильтра. В [1] описан алгоритм, изменяющий размеры апертуры фильтра: там, где есть детали (локальная дисперсия превышает дисперсию всего изображения), желательно использовать малый размер, и наоборот, там, где фон (дисперсии близки), можно проводить фильтрацию с большим размером апертуры. Для определения малости различий дисперсий предложено вычислять параметр активности, зависящий от математического ожидания и вычисляемых дисперсий. Полученный параметр активности сравнивается с некоторым порогом, после чего принимается решение об изменении размеров апертуры. Фильтрация выполняется по линейному алгоритму. Предварительно оговаривается максимальный возможный размер апертуры. Сравнение адаптивного фильтра с линейным показывает, что для адаптивного алгоритма увеличивается время фильтрации. В то же время адаптация размеров апертуры позволяет устранять импульсный шум, с чем не справляется обычный линейный фильтр. Для получения хороших результатов фильтрации требуется подобрать порог при изменении размеров апертуры.
Медианные фильтры хорошо работают, если плотность шума невелика. Адаптивный медианный фильтр даёт хорошие результаты и в случае больших плотностей шума. В дополнение к этому адаптивный медианный фильтр стремится сохранить детали, размывая при этом неимпульсный шум [1]. Адаптивный медианный фильтр, подобно описанному выше адаптивному алгоритму, возвращает или значение в данной точке или медиану, но при этом в ходе обработки размер апертуры увеличивается до тех пор, пока не будет найдена медиана, не являющаяся импульсом, или пока размер окна не превысит максимальное заданное значение. Этот алгоритм позволяет устранить импульсный шум, размыть шум неимпульсного происхождения, уменьшить искажения на границах объектов в изображении.
Выводы.
- Наиболее сложными для реализации являются алгоритмы, требующие вычисления дополнительных характеристик изображения: такие как преобразование Фурье, вейвлет–преобразования, корреляционные функции. К этим алгоритмам относятся алгоритмы, использующие частотные методы, метод Винера, метод Калмана.
- Худшее быстродействие по сравнению с линейными и медианными фильтрами имеют комбинированные и гибридные из-за многократного вычисления выхода подфильтров, а также адаптивные фильтры по причине постоянного вычисления характеристик изображения с целью выбора нового элемента или нового размера апертуры. Представляет интерес сравнить быстродействие комбинированных, гибридных и адаптивных методов между собой.
- Для устранения Гауссова шума лучше всего использовать линейную фильтрацию, оптимальным является фильтр Винера. Линейные фильтры размывают детали и самого изображения.
- Импульсный шум лучше всего удаляется нелинейными фильтрами на основе ранговой статистики, сохраняя при этом перепады в изображении. Но эти алгоритмы плохо устраняют Гауссов шум.
- Для устранения комбинированного шума используют усовершенствованные алгоритмы с учётом особенности шума, комбинированные или гибридные, а также адаптивные фильтры. Эти алгоритмы работают на основе как линейной, так и нелинейной фильтрации.
Список литературы:
- Гонсалес Р. Цифровая обработка изображений / Р.Гонсалес, Р.Вудс. – М.: Изд-во ТЕХНОСФЕРА, 2005. – 1072 с.
- Прэтт У. Цифровая обработка изображений / У.Прэтт. – М.: Мир, 1982. – 781 с.
- Яне Б. Цифровая обработка изображений / Б. Яне. – М.: Техносфера, 2007. – 584 с.
- Павлидис Т. Алгоритмы машинной графики и обработки изображений / Т.Павлидис. – М.: Радио и связь, 1986. – 396 c.
- Методы компьютерной обработки изображений / Под ред. В.А.Сойфера. – 2-е изд. испр. – М.: Физматлит, 2003. – 784 с.
- Грузман И.С. Цифровая обработка изображений в информационных системах: Учебное пособие / И.С.Грузман, В.С.Киричук, В.П.Косых, Г.И.Перетягин, А.А.Спектор. – Новосибирск: Изд-во НГТУ, 2000. – 168 с.
- Воскобойников Ю.Е. Фильтрация сигналов и изображений: Фурье и вейвлет алгоритмы ( с примерами в Mathcad): монография: Новосиб. гос. архитектур.-строит. ун-т (Сибстрин) / Ю.Е.Воскобойников, А.В.Гочаков, А.Б.Колкер. – Новосибирск: НГАСУ (Сибстрин), 2010. – 188 с.
- Бухтояров С.С. Удаление шума из изображений нелинейными цифровыми фильтрами на основе ранговой статистики: автореф. дис. на соиск. ученой степ. канд. техн. наук. по спец. 05.12.04/ С.С.Бухтояров. – М., 2007. – 20 с.
- Апальков И.В. Удаление шума из изображений на основе нелинейных алгоритмов с использованием ранговой статистики/ И.В. Апальков, В.В. Хрящев// www.graphicon.ru/2007/proceedings/Papers/Paper_20.pdf.
- Бронников А.В. Комбинированные алгоритмы фильтрации зашумленных сигналов и изображений/ А.В. Бронников, Ю.Е. Воскобойников// Автометрия. – 1990. – No 1.
- Антощук С.Г. Гибридная линейно-ранговая фильтрация сигналов и изображений/ С.Г. Антощук, В.Н. Крылов, В.О. Давыдов// Труды Одесского политехн. ун-та: науч. и произв.-практ. сб. – Одесса, 2000. – Вып.3 (12). – С. 140.
- Воскобойников Ю.Е. Адаптивный алгоритм фильтрации изображений и преобразования их в векторный формат/ Ю.Е. Воскобойников,А.Б. Колкер// Автометрия. – 2002. – Т.38. – No 4. - С.15–21.