Abstract
Contents
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. Types of methods of pricing and revenue management
- 3.1 Revenue Management. Types of companies to implement
- 3.2 Interaction subsystems in the revenue management system
- 4. Forecast model
- 6. The calculation of optimal limits sales
- 5.1 Method EMSR-b
- 5.2 Method EMSRr
- Conclusion
- Source List
Introduction
One of the ways to maximize profits in the hospitality industry is the application of Revenue Management - optimizing sales numbers by imposing restrictions on the number of rooms in different price classes. Revenue Management in Ukraine at the beginning of its development, while foreign countries use these methods since they have developed. The main objective of optimization - allocate the available resources, ie number of rooms - hotel capacity (Cap), at the price of the classes so as to maximize the total expected revenue.
1. Theme urgency
The method of revenue management is the most relevant method of pricing and building a strategy, the use of different calling plans. Revenue management came into the hotel business from the airline industry and gradually captures the market. And while abroad more and more hotels are moving to the system of real-time pricing, using the methods of revenue management, in Ukraine the situation is much worse. Only a large hotels, yet allow themselves to the development of such systems. But the example of the airline industry and in view of the profitability, it can be concluded that these methods will soon be widely used in the hospitality industry, including hotels with a small capacity.
2. Goal and tasks of the research
The aim of this work is to create a computerized system that optimizes the price of hotel rooms on the basis of curves reservation. In other words, this system is maximizing the demand from each object, through a combination of price and sales capacity.
Main objectives of the study:
- analysis of the subject area and the existing methods of pricing.
- Choosing the most effective method of pricing.
- Determination of optimal conditions for the implementation of the revenue management methods.
- Overview of the most effective methods of calculating the optimal limit.
The object of research is the process of determining the best prices in the enterprise environment of the hospitality industry.
3. Types of pricing methods and revenue management
3.1 Revenue Management. Types of companies to implement
Revenue Management (Revenue Management) - one of the ways of the forecasting and using the information systems in the hospitality industry. This is an economic technique, aimed at identifying the best pricing to optimize revenue by determining the behavior of the demand.
This method maximizes the two sources of income: the capacity and the price per unit.
Types of companies to implement such systems:
- varying demand and fixed production capacity (demand fluctuates, sometimes higher, sometimes lower than the available capacity; own capacity is limited because you can not sell the 110 rooms in the hotel, their numbering 100).
- sales by pre-booking (the sale of inventory or production capacity for some time before this date production services).
- complex pricing structure (as the demand and price flexibility varies according to different factors, the practice of differential pricing: the lower the price the additional profit generated by the involvement of customer segment, the most sensitive to changes in prices, establishment of certain restrictions on prices and sales quotas in terms of segment / price will limit the decline in the share of customers' sensitivity to price changes smallest).
- very low variable costs per unit of product or service (depending on the sector, it ranges from 0 to 20% of the total cost, so the hotel industry in the variable costs of the sale of one additional guest rooms, including housekeeping and provision of related services is a very small amount; personnel costs and depreciation charges do not depend on the capacity of sales).
- perishable inventory (services or products, which value will reset to zero after the date of manufacture; as example - the seats on the plane or the empty rooms in the hotel that have zero net worth, it is called a zero-turnover funds).
3.2 Interaction subsystems in the system of revenue management
In general, the revenue management system communicates with the multiple systems in real time. Among them are the reservation system, the registration system and the system of income. Each of the systems interact with a particular subsystem, which consists the revenue management system. The scheme of interaction of the main information systems presented in Figure 3.1
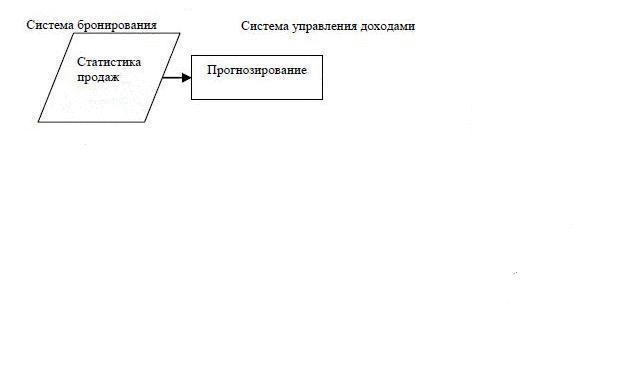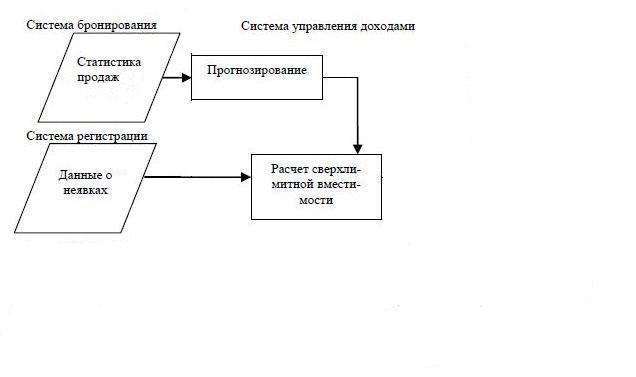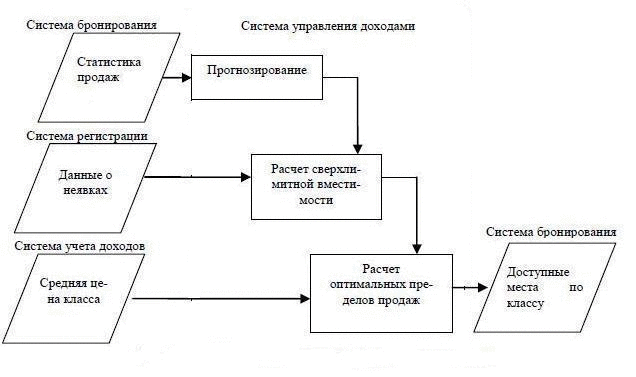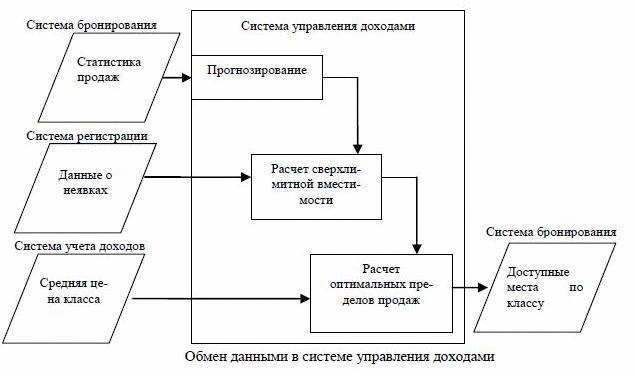
Figure 3.1 - Exchange of data in the revenue management system
(animation: 5 shots, 5 cycles of repetition, 175 KB)
4. Forecast model
The purpose of forecasting - calculating two parameters for each price class - the mean and standard deviation (for a grade μk and σk). To forecasting demand, it can be based on different sets of statistics that reflect the dependence of the capacity of reservations weather conditions available on the market of competitors, etc. But in practice, the hotel enterprises have historical data from the inventory system in which there is no additional information beyond the number of bookings and the number of seats available for sale in each class for several similar weekends / days in the past. Data collection is carried out several times - a few slices of the opening of the sale on a given date to check into a room. These slices are determined by the fact that the adjustment of sales there is no need to spend every day, but there is a need to periodically monitor the situation. Therefore, the entire horizon of sales broken down into a number of control points, which are removed when a current reading on the sale of numbers and calculated projections and outside sales. In this case, if at any time the number of available places is zero, this means that the sale is not conducted and requests for this class will be rejected. Thus, the available historical data into account only confirmed reservation, and the total number of tourists who wanted to stay unknown, that is part of the sample is censored.
5. The calculation of optimal limits sales
The goal of optimizing sales - to distribute the available resources at, ie number of rooms - hotel capacity (Cap), of price classes so as to maximize the total expected revenue from sales.
The simplest mathematical model proposed by Littlewood. It considers only two price class with the price ratio f1> f2. We assume that the demand for the lower class is formed in advance, as its price is lower and it is unlimited. The challenge is to decide how many seats should be reserved for the lower class before the arrival of tourists in the upper (more expensive) grade.
With the known average μ1 demand for top-class probability of arrival of one customer in it is very high. When you book a room for him, we get an average income equal to f1 × P (μ1 ≥ 1). Without doing this, we are guaranteed to get the revenue f2. Therefore, the decision on the reservation should be made by comparing these two income. Arguing similarly, we find that the expected benefits from the backup x-th place in the upper class will be f1 × P (μ1 ≥ 1). Accordingly, it makes sense to accept the request of the lower class (ie, not to reserve a place for the top) only if its price exceeds the potential gain from making the opposite decision:
f2 ≥ f1 × p (μ1 ≥ x) (1), Note that the right side (1) decreases with increasing x. Optimal operation is denoted y1. Thus, we take the lower class, if the residual capacity than y1, and reject it if the residual capacity - y1 or less. In case of a continuous distribution function F1 (x) y1 optimum protection can be determined more simple expression f2 = f1 × P (μ1 ≥ y1), which is equivalent to:
F1 (x) = 1 − f2/f1, which is known as the Littlewood's rule.
Hospitality businesses actually use more than two price class and, therefore, more complex models of management. Generalization of the Littlewood classes, n is the empirical method EMSR (Expected Marginal Seat Revenue), having different versions.
6.1 Method EMSR-b
Consider the most common variant EMSR-b. The algorithm for calculating the levels of protection for the price class of the day consists of several steps. In the first step, the first two are considered separately price class and Littlewood model we calculate the level of protection for the top of them. Then, these two classes are combined in a so-called super class with the price, defined as the weighted average of the prices and the location and scale parameters, calculated as the sum and the root of the sum of squares of corresponding parameters of its constituent classes. The model then Littlewood for the superclass and a third of the price class is used to determine the level of protection of the superclass, which is taken as the level of protection of the second price class. Further along the lines formed by the superclass of the first three and the calculation process continues. The final step is the calculation, which involved a superclass of all classes, except the bottom, and this very low price class.
6.2 Method EMSRr
Another approach is not based on the Littlewood. This method is intended for use in preparation forecast demand for lower class, and does not assume that the demand is not limited, as in the model of Littlewood.
The expected income from reserving one room for a tourist class k is fk × (1 − Φ (μk, σk, 1)), where Φ (μk, σk, 1) - distribution function normal distribution at x. Recall that the value of the distribution function represents the probability that the random variable takes a value smaller than x. Thus, the expected return is the product of the room to the likelihood that this number will be a buyer. The expected income from reserving two rooms in the k-th price class is fk × (1 − Φ (μk, σk, 1)) + fk × (1 − Φ (μk, & sigma ; k, 2)), and so forth.
As a result, it is possible to formulate the following optimization problem: it is required to determine the number of rooms xk, reserved in every price class k = 1, in such a way as to ensure maximum value for the total expected income, and not to exceed the specified capacity at:
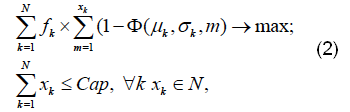
where Cap - Capacity of hotel business / hotel, and N - extended set of natural numbers (ie, all off-reservation rk - non-negative integers).
Conclusions
The procedures discussed in this paper can most accurately determine the pricing policy of the company to maximize the total revenue, and develop a strategy for further development of the hotel business. The choice of methods of revenue management for use in specific circumstances, you need to do based on computing capabilities, as well as the degree of censoring of data on which to build the demand forecast. In general, I believe that these methods more than ever, relevant and above all need of automation in the hospitality industry.
Source List
- Лапина М.Г. Восстановление реального спроса по цензурированной статистике бронирования/ М.Г. Лапина, Г.М. Фридман// Современные технологии, Москва. -2010.
- Littlewood K. Forecasting and Control of Passenger Bookings / K. Littlewood // Proceedings of the 12th AGIFORS Symposium. Nathanya. Israel. -1972. -P. 95-117.
- Talluri K.T., Ryzin G.J. The Theory and Practice of Revenue Management / T.K. Talluri, G.J. Ryzin // Springer.-2005 -P. 714.
- Weatherford L.R., Polt S. Better unconstraining of airline demand data in revenue management systems/ L.R. Weatherford, S. Polt // Journal of Revenue and Pricing Management. -2002.
- Носова Е.В. Моделирование процесса управления доходами авиакомпании на уровне рейсов / Е.В. Носова //Современные технологии, Москва. - 2009 -C. 71-75.
- Polt S. New results on leg optimization / S. Polt //Yield Management Study Group Symposium, London, UK. -1999.
- Носова Е.В. Моделирование процессов продаж билетов на рейсы авиакомпании / Е.В. Носова //Современные технологии, Москва. – 2010.
- Мозговая К.А.Расчет Компенсационной функции при продаже авиабилетов с учетом виртуальной вместимости воздушного судна / К.А. Мозговая // Известия СПБ ГУЭФ, Санкт-Петербург. – 2011.
- Leder K., Spagniole S. Probabilistically Optimized Airline overbooking strategies or Anyone willing to take a later flight?/ K. Leder, S. Spagniole // UMAP Journal 23.3, p.317-338, 2002.
- Rothstein M. O.R. and the airline overbooking problem / M. Rothstein // Operation Research Vol.33, p. 237-248, 1985.
