Эволюционные алгоритмы

Перевод: А.С. Резниченко

Источник: http://www.politespider.com/papers/general/Evolutionary%20Algorithms%20for%20the%20design%20of%20VLSI.pdf

Нам известен, только один эволюционный алгоритм для глобальной маршрутизации (Esbensen[1994]). Перед тем как начинается процесс глобальной маршрутизации, прямолинейный граф маршрутизации извлекается из заданного размещения. Маршрутизация производится в рамках этого графа, то есть глобальная маршрутизация для сети производится вычислением соответствующего пути в графе маршрутизации. Другими словами, каждое ребро графа соответствует каналу маршрутизации, и каждая вершина соответствует пересечению двух каналов. Вершины отображающие терминалы сети добавляются в соответствующие места графа. Поиск кратчайшего пути для сети эквивалентно поиску поддереву минимальной стоимости. Этот граф охватывает все добавленные терминальные вершины, предполагая что стоимость ребра определяется его длиной. Когда маршруты в сети были проложены, ее терминальные вершины убираются из графа маршрутизации, тем самым значительно уменьшая размер задачи.

Алгоритм глобальной маршрутизации основывается на двухфазной маршрутизации. В первой фазе при помощи генетического алгоритма для задачи Штайнера в вышеупомянутых графах генерируется некоторое количество различных альтернативных маршрутов для каждой сети. Затем, на втором этапе, другой генетический алгоритм выбирает конкретный маршрут для каждой сети ( из альтернатив предложенных в первой фазе), таким образом чтобы общая площадь была наименьшая.

Маршрутизатор превосходит роутер TimberWolfMC ([Сечен (1988)]), который является произведением искусства основанный на алгоритме имитационного отжига, в отношении качества решения. Однако, скорость работы меньше в 50 раз, что ограничивает практическую реализацию алгоритма.

[Lin, Hsu and Tasi (1989)] развили алгоритм разрыва связей и повторения который базируется на вероятностном перемаршрутизировании сетей с единственным результатом (роутер разрыва связей и повторения итеративно улучшает результат маршрутизации путем удаления и перерасчета маршрутов в заранее рассчитанных сетях). Начальная популяция ( состоящая из сетей в качестве индивидов) сгенерирована путем оновременно и алгоритма наименьшего пути и стратегии случайного пути. Конкурентные результаты представлены для канала и переключающих бенчмарков. Время цикла колеблется от нескольких минут для небольших примеров и до 24 часов для задач маршрутизации крупных каналов.

Маршрутизатор [Geraci ET. др.. (1991)] сочетает в себе метод наискорейшего спуска с особенностями генетических алгоритмов. Оператор скрещивания ограничен обменом между целыми сетями и процедура мутации представлена только для создания новых индивидов. Представленные результаты ограничиваются простыми проблемами СБИС, и никакие замечания по времени выполнения не даются.

Некоторые эволюционные алгоритмы были представлены для задачи маршрутизации ограниченных каналов; ; [Рахмани и Оно (1993)] дают пример такого, в частности того как это делают [Рао и д.р. (1994)] и [Рао и д.р. (1995)]. Здесь, все вертикальные сегменты расположены на одном уровне и все горизонтальные сегменты размещены на втором уровне. Эти и другие ограничения делают эти подходы неприменимыми для задачи маршрутизации каналов в реальных СБИС.

Генетический алгоритм для маршрутизации каналов опубликованный в [Lienig и Thulasiraman (1994)], основан на зависимых от задачи отображения схем. Здесь компоновка кодируется в трехмерную решетку, как хромосомы с клетками, которые представляют разные точки координации решения задачи маршрутизации. Значение ячейки указывает, какая из сетей маршрутизируется в этой точке координат в решении задачи маршрутизации. Отрицательное значение указывает на фиксированное назначение( например выхода схемы – pin) и ноль указывает на то что данная точка не используется(рисунок 8, как описано в [Lienig и Thulasiraman (1994)]).

Эта трехмерная схема кодирования гарантирует, что достаточно хорошая структура маршрутизации «маршрутизации острова» будет сохранена в виде компактных высоко-работоспособных блоков в хромосоме. Следовательно, эти строительные блоки имеют высокую вероятность быть переданными неповрежденными и объединяют с другими высококачественными блоками в потомстве решений. Кроме того, эта схема кодирования обеспечивает простой контроль маршрутизации ограничений непосредственно в хромосоме.

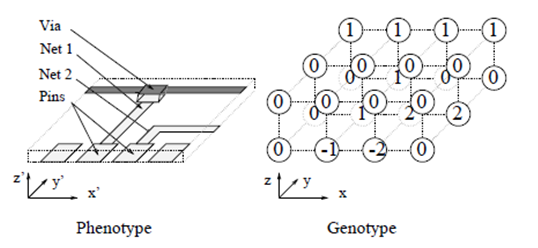
Рисунок 8 - Пример структуры маршрутизации (слева) и его генетического кодирования (справа)

Генетические операторы также специально разработанные для задачи маршрутизации каналов. Результатом являются либо качественно аналогичные или лучше чем лучшие опубликованные результаты для тестов маршрутизации каналов. Время работы алгоритма (от 1 до 50 минут) является неконкурентоспособным.

Генетический алгоритм для задачи маршрутизации канала, который включает в себя специфическую для задачи эвристику, представлена [Gockel ET. др.. (1997a)]. Представленны результаты идентичны тем, которые в [Lienig и Thulasiraman (1994)], но с более короткими временем вычисления. Расширение этого алгоритма маршрутизации каналов с более чем двумя слоями (так называемых "многослойных детализированная задача маршрутизации") также были опубликованы [Gockel и. др.. (1997b)]. Экземпляры до пяти слоев и более 60 сетей были учтены, с временем вычисления от нескольких минут до 24 часов.

Генетический алгоритм [Lienig и Thulasiraman (1996)] для распределительной маршрутизации похож на канальный маршрутизатор. Генотип, по существу соответствует решетке координат точек разметки (как в канальном маршрутизаторе). Скрещивание и мутация выполняются в рамках взаимосвязи сегментов. Алгоритм предполагает, что распределительная коробка может быть расширена в обоих направлениях. Впоследствии эти расширения уменьшаются с целью достижения фиксированного размера блока переключения. В то время как более требовательные по времени исполнения, на многочисленных примерах тестов, генетический алгоритм производит решения с равным или лучшими характеристиками маршрутизации, чем ранее опубликованы лучшие результаты.

[Lienig (1997)] представляет параллельный генетический алгоритм для задачи маршрутизации каналов и блока маршрутизации. Задача основана на теории прерывистого равновесия из [Eldrege и Gould (1972)] и [Cohoon и. др. (1991)]. Генетический алгоритм с прерывистым равновесием является параллельным генетическим алгоритмом, в котором независимые субпопуляции индивидов с их собственными функциями приспособленности развиваются в изоляции, за исключением обмена индивидами (миграции), когда состояние равновесия по всем субпопуляциям было достигнуто (см. рисунок 9).

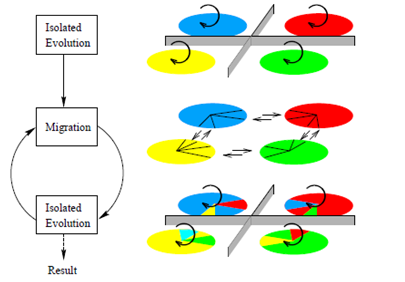
Рисунок 9 - Прерывистая равновесная модель с четырьмя субпопуляциями. Субпопуляции развиваются в изоляции («Изолированные Эволюция»), что периодически прерывается ограниченным обменом индивидами(«Миграция»).

Множество индивидов n (решения задач) присваивается каждому из процессоров N, а общий размер популяции n x N. Множество присваиваемое каждому процессор считается субпопуляцией. Процессоры соединены сетью с тороидальной топологией. Таким образом, каждый процессор (субпопуляции) имеет ровно четырех соседей.

Сперва, основной процесс создает начальные субпопуляции на каждом процессоре. Эта начальная субпопуляция состоит из случайно построенных (т.е. не оптимизированных) решений маршрутизации. Они построены по случайной стратегии маршрутизации, которая соединяет узловые точки в произвольном порядке со случайно размещающимися взаимосвязями. Основной процесс состоит из некоторого числа итераций, называемых эпохами. Во время эпохи, каждый процессор раздельно и параллельно выполняет последовательно генетический алгоритм на его субпопуляции в течение определенного числа поколений. После этого, каждая субпопуляция обменивается определенным количеством идивидов (мигрантов) с четырьмя соседями. Здесь, инидивиды обмениваются сами собой, т. е. мигранты удаляются из одной субпопуляции и добавляются к другой. Таким образом, размер субпопуляции остается прежним после миграции и ассимиляции мигрантов является просто пересчетом приспособленности. Процесс продолжается с отдельными эволюциями каждой субпопуляции в течение следующих эпох. В конце процесса, лучшие индивиды, которые существуют (или существовали) представляют собой окончательное решение маршрутизации.

Экспериментальные результаты показали, что при применении к задачи маршрутизации, параллельный генетический алгоритм - основывающийся на концепции прерывистого равновесия - работает лучше, чем последовательный генетический алгоритм.

• Небольшое количество мигрантов (от 1 до 3 на соседа) в сочетании с "умеренной" длиной эпохи (примерно от 5 до 10 процентов от общего числа поколений) приводит эвристически к лучшим результатам.
• Варьируемая длина эпохи, определяемая с помощью равновесных мер в субпопуляции, достигает общие результы, которые немного лучше, чем полученные с помощью (почти)оптимизированных фиксированных длительностей эпохи. Практическое применение этого "строгого метода прерывистого равновесия" требует, чтобы пользователь взвесил преимущества этой «самонастройки» и учел его главный недостаток, снижение временной эффективности.
• Качественные ограничения на мигрантов (например, быть выше среднего в приспособленности) не улучшают общее поведение алгоритма, а наоборот, требования к качеству на отбор мигрантов привели к преждевременной стагнации.
• При наличии достаточного числа особей в субпопуляции, большее число параллельно развивающихся субпопуляций даст лучшие результаты маршрутизации (при фиксированном общем количестве оценок). Масштабы задачи и минимальный размер субпопуляции имеют прямую корреляцию, которая должны быть принята во внимание при разделении населения на субпопуляции.

Как и размещения, все опубликованные эволюционные алгоритмы маршрутизации отличаются от "традиционных" генетических алгоритмов. Это связано со сложностью отображения схем, в силу зависимых от расположения ограничений. Генетические операторы, такие как скрещивание и мутация, включают учет правил проектирования, чтобы избежать неразрешимых конфликтов в потомстве. Значительное улучшение в качестве решения, надежность и скорости работы была достигнута с помощью стратегии параллельной реализации.

Как и разбиение, инструменты генетического алгоритма доказали свою эффективность, но, как правило, не могут конкурировать с «произведениями искусства», т.е. инструментами описанными в литературе, в критериях времени вычисления и надежности. Для обсуждения таких инструментов, см. [Sherwani (1999)].

5.4 Уплотнение

Как упоминалось ранее, уплотнение преобразует символическое расположение в маску расположения с целью минимизации размера полученной компоновки цепей. Он обычно состоит из двух отдельных шагов: (1) трансформация символического топологии в маску топологии и (2) уплотнение топологии макета. Оба шага должны быть выполнены со строгим учетом правил проектирования. Первый шаг приводит к использованию символов как представление компонентов схемы («схематические ориентированное проектрование"), которые, очевидно, не могут учесть все геометрические особенности этих компонентов. Создание маски компоновки также содержит подробные характеристики конечной технологии изготовления.

Последующее минимизации площади компоновки использует расположение областей, которые позволяют уплотнение в одно (или два) направления на основе их предназначения. (Например, площадь обычно только горизонтальные сегменты маршрута без отверстий позволяют вертикальное уплотнение.) В связи с используемой стратегией, уплотняющие алгоритмы делятся на одномерные алгоритмы (уплотнение в одном направлении за один раз), двумерные алгоритмы (уплотнение в х и у направлениях одновременно), и топологических алгоритмов (перемещение отдельных клеток в соответствии с ограничениями маршрутизации).

Насколько нам известно, единственное применение эволюционного алгоритма для уплотнения было развито в двух работах : [Фурман (1985)] и [Goodman и. др.. (1994)]. (В своей статье [Хси и др.. (1988)], использует аналогичные принципы для применения метод имитации отжига для задачи уплотнения.) В первом из них, [Фурман (1985)] описывает два прототипа генетических алгоритмов, которые выполняют уплотнение символического макета схемы.

Алгоритм учитывает символическое размещение и результаты маршрутизации, которые характеризуются их требованиями к маршрутизации и технологическими ограничениями. Эти конструкции кодируются в отдельных индивидов. Индивиды проходят эволюционный процесс с выбором на основе как количества нарушений правил проектирования и размера выделенной области.

Хотя его результат ограничен лишь очень простыми структурами макет, он делает предложение новой задачи конкретного представления для разметки проектирования, который включает в себя ограничения по процессу уплотнения. Ни время автономной работы, ни реальные приложения для проектирования СБИС не обсуждаются.

В работе [Goodman и. др.. (1994)], авторы исследуют методологии, известной как иерархическое представление хромосомы (HCR) и ее применение к нескольким связанным задачам - в том числе уплотнения. Применяя эту новую методологию для задачи уплотнения, он утверждал, что многие из ограничений и ограничений методов из [Фурман (1985)] могут быть преодолены, но обсуждение было лишь теоретическим. Нет реального кода программы или результата.

6 Выводы

Так как проблемы, возникающие при физическом дизайне СБИС очень сложные, эволюционные алгоритмы имеют значительный потенциал в этой области. Соответственно, имело место значительное увеличение эволюционных алгоритмов, которые были разработаны для СБИС приложения физического проектирования. Это развитие характеризуется некоторыми особенностями, такими как:

• Успешная эволюция алгоритмов в СБИС проектировании различаются от "традиционной эволюционной концепции алгоритма" в том, что они включают проблемно-ориентированных знаний в их операторов. Кроме того, универсальные фиксированной длины реализации двоичные часто заменяется стандартные схемы представления.
• Комбинации эволюционных алгоритмов с другими стратегиями оптимизации, например, имитации отжига или быстро детерминированных алгоритмов, больше не являеются исключением. Их введение, кажется, часто единственный способ получить подход, который предлагает конкурентоспособный по время выполнения.
• Полезные параллельной реализации эволюционных алгоритмов появились в проектировании СБИС. Повышение доступности высокоскоростных локальных компьютерных сетей и недорогой параллельных компьютеров способствует реализации параллельных эволюционных алгоритмов с улучшенным качеством раствора и характеристиками времени вычисления.

Хотя эти тенденции выглядят многообещающими, они не могут быть проигнорированы, что большинство эволюционные алгоритмы на основе СБИС не применимы в реальных системах проектирования СБИС. Это условие указывается благодаря тому, что в настоящее время существует коммерчески доступные системы EDA , которые не содержат любой эволюционный основы алгоритма.

Каковы причины этого очевидного конфликта между обещаниями для разработки новой технологии решения и его проблемы успешного внедрения? Одно расследование [Lienig (1996)] с различными поставщиками программного обеспечения показал два основных недостатка эволюционных алгоритмов: надежность и неоправданные ожидания. Эволюционные алгоритмы имеют вероятностный характер, а значит, одно исполнение не обязательно предоставляет наилучшие результаты. Это свойство является одной из причин, что многие очень хорошие результаты, утвержденные в публикациях, не могут повториться в последовательных экспериментах с использованием практических приложений - часто только "тонкая настройка" некоторых параметров привело бы к ожидаемым превосходным результатам.

Эти и другие причины ответственны за разрыв между успешными академические результаты с основанными на эволюционной модели алгоритмов физического проектирования СБИС и очевидное пренебрежение этими алгоритмами в коммерческих инструментах проектирования. Тем не менее, мы считаем, что вышеупомянутые проблемы можно избежать, если следующие рекомендации принимаются во внимание при разработке эволюционных алгоритмов для задачи проектирования СБИС:

• Поскольку эволюционные алгоритмы вероятностных подходов, является очень важным исследовать влияние случайности на качество решения. Проектировщик СБИС всегда подумает перед использование алгоритма, который должен отработать несколько раз для достижения реально используемого и конкурентноспособного результата. Кроме того, параметры, используемые для запуска эволюционного алгоритма должны быть ограничены так, что они могут быть легко приспособлены к конкретной проблеме конструкции без длительных экспериментов.
• Вероятностный характер алгоритма следует обсудить, когда бы ни присутствовали решения эволюционных алгоритмов. Другими словами, необходимо четко выразить, как представленные результаты были получены. Случайность результаты также должна быть принята во внимание, при сравнении времени вычислений эволюционного алгоритма с другими алгоритмами, которым необходима всего одна итерация для достижения результата.
• По возможности, представленный подход следует сравнивать с самыми лучшими алгоритмами в отношении как качества решения и так и времени выполнения. Многие из исследованных эволюционных алгоритмов являются конкурентоспособными по отношению к базирующемуся только на качестве решению. Тем не менее, представляет интерес в области проектирования VLSI, измерение времени вычисления работы также должны быть использовано. Менее интересным для общества является число рекомбинаций, число посещенных точек в каждом пространстве, и так далее.
• Ограничения других алгоритмов должны быть приняты во внимание при сравнении с их результатами. Например, это не справедливое сравнение, когда маршрутизация качества эволюционного алгоритма выражается только с точки зрения числа межслойных отверстий ([Geraci ET. Др.. (1991)]), а затем сравнивается с результатами других подходов, которые минимизируют чистую длину одновременно.
• В связи с большим количеством САПР в проектировании СБИС, исходные данные доступны для всех основных этапов проектирования, например, [Тесты EDA (1997)]. Эволюционный алгоритм, разработанный для проектирования СБИС не создаст никаких интересов внутри сообщества СБИС, если его работа не будет протестирована с соответствующими контрольными показателями. Только путем изучения результатов этих бенчмарков, мы можем сравнить конкретного эволюционный алгоритм с любым другим(любым) подходом. Тестовые примеры должны быть большими, что отражает реальные проблемы СБИС.

7 Подведение итогов

Мы представили исследование эволюционных алгоритмов, которые были применены в физическом проектировании СБИС. Мы также предоставили руководящие принципы, чтобы эволюционные алгоритмы были более конкурентоспособным среди физических алгоритмов для проектирования компоновки СБИС. Мы считаем, что такой подход является важной и необходимой частью дальнейшего развития этой области.