Abstract
Jian Ding and George Sperling. A gain-control theory of binocular combination.
A wide variety of visual recognition systems are developed for precise tasks and types of objects. In this paper we would like to emphasize ways to build a more generic recognition system. Perception is one of these mechanisms that psychologists particularly pointed out as a fundamental one for actively organizing and making sense of input sensory information. Based on psychological assumptions, we propose to explore the concept of perception, infer formalization in the dynamical system framework and quantitatively analyze it on robotic platforms using a unique simple neuronal architecture based on the association of visual and motor information (movements of the body or part of the body). This coupling of sensory flows of information can be characterized by a sensorimotor invariant, a dynamical attractor that we identify as a perception function. For place, object or facial expression recognition, we show how simple sensori-motor architecture can be applied to accomplish each task in terms of behavioral recognition. In each application, some pertinent visual information, based on classical focus point detection, are organized as local views and associated to an action or an internal state corresponding to a set of actions, in order to reach a location, an object or recognize a facial expression. The active learning phase for different points of view or face expressions allows the emergence of a stable perception linked to a stable sensori-motor attractor and allows the robot to perform a stable behavior in very different initial conditions. We will show how the attractor/perception emerges during the learning phase and evaluate its spatial generalization properties.
Index Terms — Object Recognition, Active Vision, Biological Control System, Mobile Robot Dynamics
1 Introduction
Inspiration from biological systems points out new approaches and new strategies to perform tasks that are difficult to achieve on artificial systems. Modelisation and simulations on robotic platform allow to stretch these solutions in real conditions and see if or until which limits they are efficient. We will follow this approach to seek for new ways to handle the recognition problem as numerous systems seek to more and more autonomously process the rich visual information in a non-friendly, changing environment, under time constraints and objects and human interactions. In psychology, perception is known to be one of the fundamental mechanisms that organizes and makes sense of input sensory information. It is different from classical recognition as no labeling is performed. Moreover it can’t be confused with the passive processing of visual inputs into an internal model as it refers to an active process, emerging from the agent interaction with the environment (enactive approach [20]) and that can be slowly or quickly modified as the agent keeps its interaction with the environment. One can observe that human’s or animal’s perception is very stable for a wide variety of environments, objects and tasks even in changing conditions. Moreover variations in proximal sensory stimulation from a same object that grandly affect the information and limit the efficiently of direct processing of the visual flow of information is well handled. The interactions between environment and system are not all known in advance as the environment is not supposed to be controlled by the system. Hence it is a challenge to develop systems which support perturbations, short term changes and long term modifications. In this paper, we will show how to endow artificial system with a neuronal architecture allowing perceptual capacity to emerge. Different real cases will be investigated: place perception in a homing task, object view perception in an object reaching task and face expression perception in an imitation task. But for all these cases we propose to use a unique neuronal architecture to learn the sensori-motor coupling. Finally consequences on the way to process the visual information flow and properties of the behavioral recognition will be discussed.
2. Modelisation of Perception
2.1. Insights from psychological studies
All of the psychological research carried out in the perception genesis context clearly shows the necessity of an active user to constitute the perception of objects or scenes. This is especially demonstrated in experiments using a system known as sensory substitution technologies which transforms stimuli suitable for a sensory system into stimuli for another sensory system. For example, the TVSS, Tactile Vision Substitution System, used by Bach-y-Rita [1] makes it possible to convert an image collected by a video camera into a tactile image, a matrix of 20 x 20 tactors that is placed on the subject skin (on the back, thorax,..) Equipped with the TVSS and only if actively handling the camera, the subjects (complying people or blind persons) are quickly able to discriminate oriented lines and to indicate the direction of the movement of moving targets. With a more significant active training, simple geometrical patterns, and even usual objects placed in various orientations can be recognized. One absolute essential observation is that the capability of pattern recognition is accompanied by the experience of the externalization of percepts. In fact, at the beginning when the user is passive, he only feels successive stimulations on his skin. But after a training session, the user ends up forgetting these tactile feelings to remotely perceive distal stable objects in front of him.
This type of experiments clearly shows that with training, a subject can constitute a new perceptive capability once he actively handles the artificial sensor collecting the external information and forgets the sensation as if he does not have to decode them anymore. Thus the perception reaches a particular status in regard to the sensation. Perception cannot emerge from only the sensations (tactile in the TVSS case). There is no perception without action. Perception is constituted by the sensorimotor loop which binds action and multimodal reafferent signals. The sensory feedback does not deliver directly and completely the form but forces or guides the coupling and support motor-sensory or gestural invariants. The subject must control his activity and through this activity can access his agency, his gesture and the effects of his gesture.
2.2. Formalization in the dynamical system framework
Inspired by the TVSS experiments and studies on perceptive exploratory strategies [18, 17], aiming at the modeling of perceptual mechanisms, we propose to pursue a formalism of the perception in a sensorimotor context. The work in [13, 14] already assumes the emergence of perception from sensorimotor contingencies laws and more precisely considers perception as the cognitive access to the co-variation laws ruling sensations and actions.
Since the perception emerges from a dynamical coupling between the sensations and the actions, and more globally between an agent and its environment, the framework of dynamical systems seems to be appropriate to derive a definition of perception. It highlights the tight coupling between an agent and its environment via the sensorimotor loop: according to agent actions, its sensations are modified. This coupling between the agent and the environment was already developed by Gibson [7] in its ecological view of perception and Varela [20] in the concept of enaction. More precisely, Gibson suggested that the perception comes from the occurrence of sensorimotor invariants that the agent has to capture in its environment. Thus being active allows the animal (agent) to find these invariants Thus we suggest that perception should be tightly linked to the presence of an attractor generated by sensorimotor invariants. In addition as the interaction between the agent and its environment is maintained, a specific perception emulated by some current sensations, will maintain the agent in an efficient behavior and thus will control the actions of the agent.
Based on these considerations, we propose to define the perception of a cognitive system as an emergent function Per of a sensori-motor invariant and such as the action vector Ac of the cognitive system is the result of a gradient operator over the scalar function Per according to the sensorial information Sen (vector of n components) and the hidden internal state s of the cognitive system:
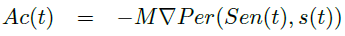
with \/ (the nabla symbol) denoting the vector differential operator (defining a vector field) andM a transformation matrix allowing a selection of the sensations in regard of the possible actions of an agent (taking into account the agent body characteristics, etc...). In consequence, considering Ac as a vector field, its inverse gradient Per is defined as the scalar function which brings the cognitive system in a minimum energy state. In the framework of dynamical systems and motor control, [10, 15] already proposed to consider the action as the derivate of such a potential function. Per can be seen as the integral over the sensation along the whole sensation space :
with Per only determined up to a constant which can be chosen arbitrary.
The minimum of the Perception function is associated with an attractor. As the notion of stable behaviors is related to the presence of stable attractors, one wants to know whether the solution is stable or not. If one looks at a fixed point attractor, one way to assure the existence of a stable one is to prove the existence of a function, namely a Lyapounov function, which decreases along all possible trajectories at least on a subspace of the sensorimotor system space. The convergence of the system to a stable state is seen as the decease of energy in the system during its evolution. It can also be seen as a ball rolling down a hill constituted by a potential function, namely the Perception function (fig. 1) [2]. From this potential function a potential field can be defined. Finally, to assure the stability of the system, the Per function results of the learned sensorimotor invariant patterns and the action of the system is derived from the Per function. A stable perception can emerge and consequently a coherent behavior of the agent in its environment is observable. The learning capabilities of the system allow to improve its behavior due to its generalization properties as we will see in the following section.

Fig. 1. Trajectories converging towards a fixed-point attractor A and the corresponding potential function (in 1D only)
2.3. A neuronal sensori-motor architecture
The goal is to sum up in a generic architecture the necessary mechanisms for the emergence of a percept in an agent in interaction with its environment. We propose to investigate a simple neuronal architecture named PerAc which was proposed to solve a wide variety of control problems requiring learning capabilities. Previously developed in [6], it was studied with a special formalism used to describe robotic architectures [4]. To fully use the sensori-motor loop, the output architecture is an action Ac which, when performed by the agent, affects the sensation inputs (fig. 2). We consider two different sensation vectors Sr and Sg. Sr represents a coarse feedback information from the execution of the motor command, namely proprioceptive information, or can be an external signal in a supervised case. Sg represents a more global and rich information (as visual one) about the environment. To be useful, this information needs to be organized. A robust distance measure on local visual features extracted from the visual flow, namely exteroceptive features, is computed and learned by a competitive group with output activity R categorizing the local features. The operator c1 represents a soft competitive structure WTA (Winner Takes All) able to self-organize according to one sensory data flow. Hence, after the competition, the activity of R reflects the categorization level. Finally the two inputs path are merged at the motor level allowing the learning of some sensori-motor coupling laws. More precisely, the ”one to one” connections (one input is definitely connected to one and only one output) between the sensations Sr and the motor command Ac generates a reflex behavior. It can be considered as a regulatory pathway linking a proprioceptive sensor to the motor command. Before any learning happened, this path is the one controlling the action. At the motor level the operator c2, another soft competitive structure, allows to condition the rich input data flow Sg, via the categorization group R, according to the unconditional flow coming from Sr. Finally we can remark that no direct visual recognition is performed (only a local categorization). The system behavior does not directly depend on the absolute level of categorization of the learned exteroceptive features. The decision is delayed until the final competition. Recognition in such a system must be understood according to the global temporal dynamic of the system. This especially allows the system to have good generalization properties. The proprioception pathway allows to structure the learning and the organization of the exteroceptive information, while the pathway with the exteroceptive information as input allows the spatial generalization of the learned behavior. This generalization not only depends on the visual features and their learning but also on the competition mechanism between actions at the motor level. In fact this competitive mechanism has great importance for the definition of a robust perception as only the rank of a competition process matters. While classical systems fail when the noise or perturbation oversteps an absolute recognition threshold, the behavior of such a sensorimotor system is robust until some perturbation affects the rank in the competition mechanisms. An illustration of a very basic sensorimotor associations and the resulting perception function Per are shown on fig. 3. It results from an object centering behavior in the agent visual field and hence the percept of the position of the object relative to the agent is studied. If the object doesn’t move in the environment, after each action of the agent, the agent state is characterized by its position relative to the object learned: the sensation vector is reduced to this position. In a one dimensional space, at two different positions (place1 and place2) on each side of the center position (goal) are first associated two antagonist actions, ”go left” (negative Ac) and ”go right” (positive Ac) in order to reach the center. The further away the agent is from one of the place where it has learned a couple sensation/action, the less activated are the neurons of R and consequently the neurons of Ac. In order to compute the Per function, let us consider the evolution of a dynamical system ruled by the generic equation: dx/dt = f(x). In the simplified case of fig. 3, we consider dx/dt = Ac, with Ac the actions performed by the robot to go from an x-coordinate to another one and allowing going from one sensori-motor state to another one. Also as we earlier admitted the action derives from the Per function, in a one dimensional space, we can write Per(x) = -Integral(Ac(U)du) and we can easily verify that the function Per is a Lyapunov function. In consequence, by integrating the actions over the visual space, we have a way to compute and to plot the perception of the agent. Fig. 3 - Right shows the computed perception function Per resulting from the numerical integration of the curve showed on fig. 3 - Center representing the actions to be performed in order to reach the center position. It presents a basin curve with a single minimum guiding the system towards the central goal location The perception allows the system to have a coherent behavior (going towards the center) whatever position it initially has.
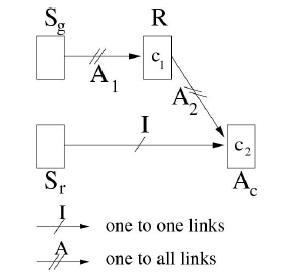
Fig. 2. A neuronal sensorimotor architecture PerAc from [6]). Sr, Sg, R, Ac are neurons vector representing the 2 sensation inputs, the learned categories and the possible output actions. A1, A2, I are connection weights matrixes and c1, c2 represent operators associated to group of neurons.

Fig. 3. Left Theoretical R level in two different locations. Center Theoretical actions Ac (speed vector of the system with the sign being the direction) after learning 2 sensation/ action associations and their competition according to the system position. Right Theoretical perception computed by integration of the Theoretical action.
3. Place Perception in a Homing Task
The neuronal architecture PerAc was initially used for a homing situation where a robot returns to a place without being able to statically recognize it [5]. The details of the neuronal architecture used in inside and outside experiments are described on the fig. 4. It shows the merge of the two sensorial paths at the level of the Movement direction group of neurons, initiated by the reflex path using the Target direction information. The Sg-R path seen on fig. 2 results here in a learned Place cell group of neurons. In order to generate a robust behavior a specific model of visual place cells, inspired from what and where functional theory of the cortical pathway downstream the hippocampus [19, 9] was developed. A place is defined by a spatial constellation of online learned visual features corresponding to a set of triplets landmarkazimuth- elevation. The different process to learn the activities of the Place cells are illustrated on the fig. 4. From a panoramic image the visual system autonomously extract landmarks by computing the gradient from the CCD input. This gradient image is then convolved with a DoG (Difference of Gaussian) filter to detect robust focus feature points at low resolution. A competition between the feature points enables the system to primarily focus on the most activated focus points (activity based on a contrast and edge curvature criterion). A small image, named local view, of a given circular area around each focus point is extracted and transformed in log-polar coordinates to enhance the pattern recognition when small rotations and scale variations occur [16]. During the learning of a place, each local view in log-polar coordinates is considered as a landmark prototype for the system. Otherwise each landmark neuron activity expresses how close is the current local view from the learned prototype. They provide the ”what” information that models the temporal pathway. The elevation or absolute angular position of the landmarks provides the ”where” information relative to a vestibular information or a visual compass [8] that models the parietal pathway. The azimuth or absolute direction is usually obtained with a magnetic compass, even if it is not strictly necessary and a local reference (such as the bearing of a distant landmark) was shown to be a sufficient estimation of the robot orientation to infer correct place recognition. Each azimuth and elevation neuron has a favorite firing direction and expresses how near is the current extracted local view from its favorite direction. The merging of this what and where information is performed in a product space (i.e. a third-order tensor compressed into a vector of product neurons. The multiplicative merging realizes an analogical ”AND” operation. The recruited merging neurons characterize a point (or a region) in the landmark-azimuth-elevation space. At the end of a visual exploration, the set of activated merging neurons defines a place-code which can be learnt as an invariant representation of the location on a new place-cell (PC). The whole architecture is bootstrapped by a vigilance signals which allows the one shot learning of all the extracted landmarks in the current location (except the ones already encoded), the building of the corresponding constellation and the recruitment of a new place-cell. At the merging level, each PC is associated with a movement to trigger when being recognized (purely reactive behavior). If the PCs and the actions are defined in the frame of a competitive structure, a minimum of three place-action associations around a goal creates an attraction basin, enabling the robot to return to the goal from each place in the attraction area (fig. 5). The robot is seen as a dynamical system in which the learning modifies the parameters. Learning is equivalent to shape this basin [12]. Step after step, the robot reacts according to the learned sensory-motor dynamics, as a ball rolling deeper and deeper in a valley. Neither Cartesian nor topological map building is required. The system builds its own metrics based on the parallax and the recognition of the landmarks. Hence, the dimensionality of the internal representation is not given by the metric size of the explored area but rather by its visual regularity. Finally the place-action associations built by the competitive architecture allow a homing behavior with a relatively good precision. We show in [9] that to improve the robustness of the place recognition algorithm the use of a soft competition allowing several interpretations of an extracted local view was essential. Fig. 6 shows how soft competition can enlarge place fields and allows them to overlap. As the final decision is delayed at the motor level, this multitude of interpretations is possible and even is favored to assure good generalization capabilities.
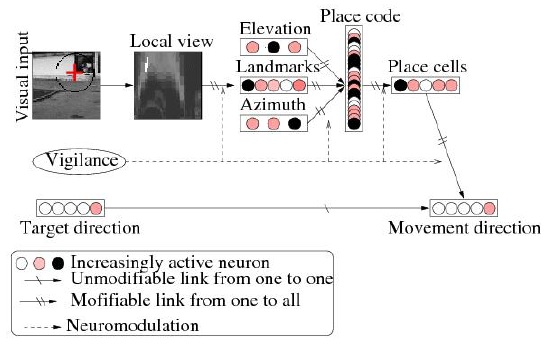
Fig. 4. PerAc architecture for a homing task. The Target direction and Movement direction are competitive groups.

Fig. 5. Top view of an indoor environment with superposed theoretical place fields and homing trajectories for four initial robot positions. 8 places (black circles) were first learned at 1m from the goal.
4. Object Perception in a Reaching Task
In the homing case, the invariants and the resulting perception were commonplace since the sensations are constant at a given place and a unique action per place is provided. In order to apprehend the object perception case, we propose to study it in a simplified version where still few dimensions are used for the sensations and actions spaces but where more complexsensorimotor laws are introduced. The task of the robot is to reach an object whose sensorimotor coupling laws have been learned during a training phase. In particular the obtained behavior has to be completely independent of the object location in the room. Only the sensorimotor laws directly related to the object have to be learned by the robot. Returning to a given object will be interpreted as the fact that the robot “perceives” the object. The robotic experiment use a Koala robot equipped with a CCD camera with no explicit static recognition of the object. The global architecture of the robot is presented on fig. 7. In order to provide useful but simple sensorimotor associations, the visual features extracted from the visual flow must be robust enough regarding the robot task. As the robot moves towards an object in unknown environmental conditions, it has to face large non-linear transformations of the images (scale, perspectives, etc.). To partially achieve scale, contrast and luminance invariance, key points are extracted on the input images (fig. 7) by a multi-scale algorithm inspired by Lowe’s work [11].
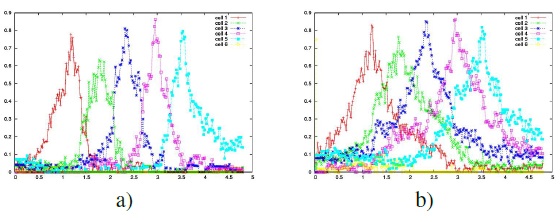
Fig. 6. Place cells activity computed every 2 cm over a line of 4.8m long and induced by a strict (a) or a soft (b) competition.
Following is a mechanism supplying a coarse local feature at each key point at the scale where the key point is extracted. For each key point only the two first moments of the orientation of the four neighborhoods relatively to the main orientation are kept. Finally, the association is performed by a conditioning mechanism based on the classical LMS (Least Mean Square) algorithm. In this group of neurons the weights associated with stable sensation/action couples are reinforced. Thus if the target object is placed on different backgrounds, only the visual features related to the object are stable. The weights associated with these features grow up sufficiently to generate a motor action. The final decision of the performed action is given by a competitive neural network WTA (Winner takes All). After only two headings “left” and “right” repeated on two different backgrounds, the robot is able to reach the learned object. In addition the perception function Per of the robot is a posteriori computed. The state of the robot is defined by its spatial location in the environment and by its body and CCD camera orientation relative to the learned object. According to our definition of perception, we propose to visualize the Per function by experimentally computing the integral of the actions performed by the robot over the 2D space. This allows to visualize the Per function for each position and so for each sensation/action couple. In addition by computing the Per function at different training steps, the role of the learning phase, shaping deeper and deeper the attraction basin, is essential in the perception genesis.
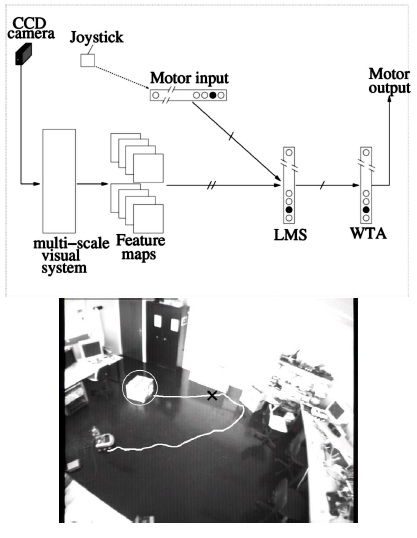
Fig. 7. top: The sensori-motor architecture. bottom: Trajectory of a robot performing an object reaching task. The object enters the robots visual field only at the black cross position.

Fig. 8. left: Top view of 2 robot positions and associated actions during learning phase.right: Final Perception function in function of the robot position.
Thus the learning can be considered as the emergence of a potential function allowing the robot to create a sensorimotor attractor. The learning allows to “dig” the potential function and consequently the robot behavior is more stable in the presence of distractors in its visual field. The learning also allows enlarging the sensorimotor attraction basin. Thus the robot behavior is less dependent on the initial spatial position of the robot in the room since at all the position in the attraction basin created during the training the robot can reach the object (experimentally the attraction basin measures 4x5 meters).
In the case of fig. 9 two similar objects are set closely to each other, but only the circled one was previously learned. We surprisingly observed that the robot has a stable behavior successfully reaching the learned object independently of its starting spatial location and even if the neurons activities coding the robot’s actions (“right” or “left” headings) can be quite similar. As the coarse features didn’t allowed a good discrimination of the two objects, we observed a change in the robot orientation relative to the target that could explain the global, behavior of the system. The display of the Per function processed over the 2D space for two different orientations of the robot confirmed our intuition. On fig. 9 top-right, we can see that the Per function has two local minima although for another body orientation only one deeper minimum is visible (bottom-right). This change of orientation was enough to disambiguate the visual flow. Unfortunately the 4 dimensional basin cannot be easily display and each of the Per function plot in this paper is drawn relatively to one orientation of the robot. This experiment clearly shows how essential it is to consider all the dimensions of the context in order to capture the sensorimotor invariant.
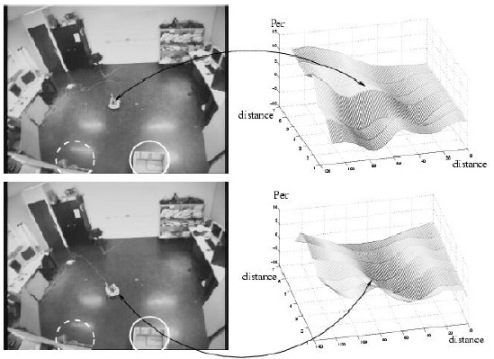
Fig. 9. The perception function (on the right) is dependent on the position of the robot but also on its orientation (on the right)
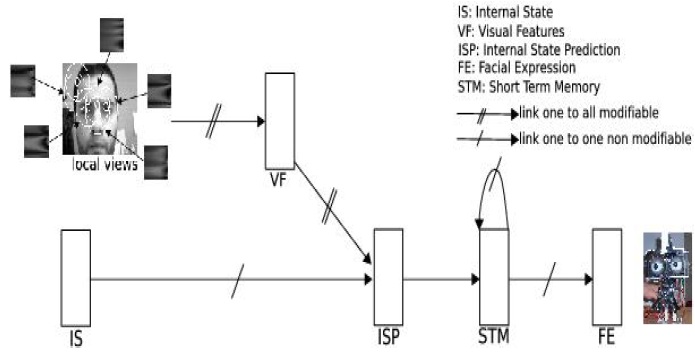
Fig. 10. Global architecture of facial expression perception)
5. Face Expression Perception in an Imitation Task
In a special paradigm of communication and imitation (see [3] for details) between a robot head and a human, a face expression recognition system is developed with the sensori-motor approach. In a first phase of interaction, as the robot produces a random facial expression (sadness, happy, anger, surprised), the human subject facing the robot is asked to mimic the robotic head expression, allowing its neuronal system to learn the sensori-motor associations between its visual sensations, the images of the human face, and its internal state, referring to its current proprioception as it is performing a facial expression. After this first phase, the robot must be able to mimic the facial expression of the human partner showing by this behavior the success of the human expression recognition. Based on the PerAc architecture, the computational architecture on fig. 10 allows to recognize facial expressions and imitate them. Each group of neuron IS, ISP, STM and FE contains 5 neurons corresponding to the 4 facial expressions plus the neutral face. In particular we recognize the two sensorial paths merging in the Internal State Prediction group ISP. This group learns, via a simple conditioning mechanism using the Least Mean Square (LMS) rule, the association between the Internal State group IS showing the emotional state and the Visual Features group V F that learned the local views. In fact the visual system is based on a sequential exploration of the image key points that result from a DOG filter convolved with the gradient of the input image. This process allows the system to focus more on the corners and end of lines in the image (eyebrows, corners of the lips, etc). One after the other, the most active focus points of the same image are used to compute local views: either a log polar transform centered on the focus point or a features extraction from a Gabor decomposition is performed to obtain an image more robust to small rotations and distance variations. This collection of local views is learned by the recruitment of new neurons in the V F group using a k-means variant allowing online learning (both one shot learning and long term averaging) and real time. After the learning phase, the associations between the V F group and ISP group are strong enough to bypass the low level reflex activity coming from the IS group. In this case, the activity of the Facial Expression group FE will result from the temporal integration (Short Term Memory group STM) of the emotional state associated to the different visual features analyzed by the system. Each focus points vote for the recognition of a given facial expression as each facial expression is mainly characterized by a specific set of focal points corresponding to local areas on the face which are relevant for the recognition of that expression. It follows that the robot head can imitate the human’s facial expression as in fig. 11. As there is no constraint on the selection of the local views (no framing mechanism), numerous distracters can be present either in the background or on inexpressive parts of the head and can be learned on the V F group. Nevertheless, the architecture will tend to learn and reinforce only the expressive features of the face. In our face to face situation, the distracters are present for all the facial expressions so their correlation with an emotional state tends toward zero. Moreover the system shows interesting properties as shown on fig. 11. The robot successfully imitates the facial expressions when facing unknown faces and even when the interaction distance is important. So even with no framing, we can see that the system had learned to discriminate background information from relevant visual features of the face. Indeed this sensori-motor face expression recognition system is a good candidate to bootstrap a sensori-motor face recognition system, see [3] for a detail analysis.

Fig. 11. Joy expressions on unknown faces and at different distances are successfully imitated by the robot head.
6. Conclusion
Providing to our robots sensori-motor architecture to control their movements, we demonstrate for three different cases how action is central to efficiently perform a recognition task. It not only provides another point of view but allows the organization of the complex visual flow of information, and the selection of relevant information in function of the task. The agent learns to decide on its own what to react to, what is relevant, what to learn. Stable and adaptable behaviors of the agent that learns from its own perspective in interactions with complex environment leads to a behavioral recognition of the context and not a symbolic recognition. In fact using the term perception is more appropriate as the agent will not perceive the same way (not the same attractor) if a different task had to be performed facing the same target (as turning away of an object instead of reaching it). We favor minimal robotic set-up and coarse visual features as it is interesting to test which are the really important features for the recognition task. Fortunately only the rank of the key points matter not the recognition level allowing our systems to adequately behave in their environment. But in fact more complex visual processes could be used in order to increase the stability of key points and of the local view features for different scale, orientation, texture conditions. In addition an attentional system would be a useful complementary mechanism to increase the level of interest of some part of the image or features. Finally an internal measure of perception is not easily grabbed, but from our modelisation an internal signal could be processed. A code, representing the whole invariants information, could be built from the pertinent local views information and their associated action specified by the task. This code could be then categorized to give access to an internal percept.
References
- P. Bach-y Rita. Brain mechanisms in sensory substitution. New York, Academic Press, 192.
- A.M. Bloch, P. Crouch, J. Baillieul, and J. Marsden. Nonholonomic mechanics and control. Interdiscplinary Applied Mathematics. Springer-Verlag, 2003.
- S. Boucenna, P. Gaussier, P. Andry, and L. Hafemeister. Imitation as a communication tool for online expression learning and recognition. IROS, 2010.
- P. Gaussier. Toward a cognitive system algebra: A perception/action perspective. In European Workshop on Learning Robots (EWLR), pages 88–100, 2001.
- P. Gaussier, C. Joulain, J.P. Banquet, S. Lepretre, and A. Revel. The visual homing problem: an example of robotics/biology cross fertilization. Robotics and Autonomous Systems, 30:155–180, 2000.
- P. Gaussier and S. Zrehen. Perac: A neural architecture to control artificial animals. Robotics and Autonomous System, 16(2-4):291–320, December 1995.
- J. Gibson. The Ecological Approach to Visual Perception. Houghton Mifflin, Boston, 1979.
- C. Giovannangeli and Ph. Gaussier. Orientation system in robots: Merging allothetic and idiothetic estimations. In Proc of the 13th Int. Conf. on Advanced Robotics, pages 349–354, Jeju, South Korea, 2007.
- C. Giovannangeli, Ph. Gaussier, and J.-P. Banquet. Robustness of visual place cells in dynamic indoor and outdoor environment. International Journal of Advanced Robotic Systems, 3(2):115–124, jun 2006.
- J.A.S. Kelso. Dynamic patterns: the self-organization of brain and behavior. MIT Press, 1995.
- D.G. Lowe. Distinctive image features from scaleinvariant keypoints. International Journal of Computer Vision, 2(60):91–110, 2004.
- M. Maillard, O. Gapenne, Ph. Gaussier, and L. Hafemeister. Perception as a dynamical sensori-motor attraction basin. In Capcarrere et al., editor, Advances in Artificial Life (8th European Conference, ECAL), volume LNAI 3630, pages 37–46. Springer, 2005.
- J.K. O’Regan and A. Noe. A sensorimotor account of vision and visual consciousness. Behavioral and Brain Sciences, 24(5):939–1031, 2001.
- David Philipona, J. Kevin O’Regan, and Jean-Pierre Nadal. Is there something out there? inferring space from sensorimotor dependencies. Neural Computation, 15(9):2029–2049, 2003.
- G. Schoner, M. Dose, and C. Engels. Dynamics of behavior: theory and applications for autonomous robot architectures. Robotics and Autonomous System, 16(2-4):213–245, December 1995.
- E. Schwartz. Computational anatomy and functional architecture of striate cortex: A spatial mapping approach to perceptual coding. Vision Research, 20:645–669, 80.
- N. Sribunruangrit, C. Marque, C. Lenay, O. Gapenne, and C. Vanhoutte. Speed-accuracy tradeoff during performance of a tracking task without visual feedback. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 12(1):131–139, 2004.
- J. Stewart and O. Gapenne. Reciprocal modelling of active perception of 2-d forms in a simple tactile-vision substitution system. Mind and Machines, (14):309–330, 2004.
- J. Stewart and O. Gapenne. Reciprocal modelling of active perception of 2-d forms in a simple tactile-vision substitution system. Mind and Machines, (14):309–330, 2004.
- F. Varela, E. Thompson, and E. Rosch. The Embodied Mind. MIT press, 1993.