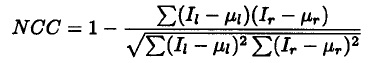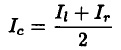X. Roca, J. Vitrih, M. Vanrell, J.J. Villanueva – Gaze Control in a Binocular Robot Systems

Abstract

X. Roca, J. Vitrih, M. Vanrell, J.J. Villanueva. Gaze Control in a Binocular Robot Systems. The ability of certain animals to control their eye movements and to follow a moving target has largely been focused in biological research. This article examines the problem of gaze control on a moving object manipulating the degrees of freedom of an active platform, without requiring the ability to recognise the target. Following the theoretical framework established by the active vision paradigm it has been designed and developed the CVC-I1 head-eye system which b an anthropomorphic head with 6 optical and 4 mechanical degrees of freedom formed by standard components. Generality, reliability and real-time performance are the main goals of the algorithms to control each of the basic visual processes. The designed strategy of these processes are based on several aspects of biologic wisual system, binocular geometry and motion decomposition. Finally, we build a mobile platform, Guidebot, to experiment with some of higher visuals tasks as time to contact, navigation and following a moving target.

1. Introduction

Computer vision deals with the analysis of images in order to achieve results similar to those obtained by the humans. Towards this objective, some computational theories and algorithms dealing with internal representations have been developed [l]. This approach has obtained important results. Other paradigms in computer vision prefer to consider the visual system in the context of the behaviour of a robot interacting with a dynamic environment. These ideas were the base for a paradigm that has been established under the term active vision. First pioneers on active vision were Bajcsy [2], Aloimonos et a1 (31 and Ballard (41, they explained from different viewpoints the advantages of the interaction between sensors and motors. Sensors provide perception to inform the creature’s behaviour, and motors make the creature an active observer using its sensors to get the maximum advantage.

The system that governs the eye movements is known as the oculomotor control system. The oculomotor system is composed by a set of basic movements, the more important are:

Optical movements: focus.
Eye movements: saccade, smooth pursuit and vergence.

All these movements cooperate in several visual tasks to perform a set of visual behaviours, such as fixation and holding. Generally, the control and coordination of eye basic movements to perform these visual behaviours is known as gaze control.

In this paper, we firstly describe different algorithms to perform the basic movements of the oculomotor system. Secondly, we present a model of gaze control in order to co-ordinate these basic movements. Finally, we propose a set of examples of visual tasks to show feasibility of gaze control algorithms. The results of the visual tasks are tested on a mobile platform.

2. Focus

In computer vision, and also in biological vision, is important to acquire sharp images to extract information from the images, because defocused images have less information than sharply focused images. Moreover, one can derive depth information from focusing. We have developed an auto-focusing algorithm whitch enables the optical system to focus on an object in a scene even when the object is moving.

Our algorithm [5] is divided in two parts:

Computing a measure of defocusing. For this part we chose the dynamic focus criterion (DFC) [6]. This criterion is computed by comparing (point to point) the grey-level values of two images instead of comparing the energy of the first or second derivatives.
Applying an algorithm that controls the lens movements towards the best-focused image, we propose an optimal search algorithm to find the best focused image using the DFC. Optimality is given in terms of the number of lens movements. The algorithm does not only consider the unimodal property, as the classical Fibonacci search does [7], but it also considers the symmetry of the criterion function.

In the figure l(a) we can see a set of images taken out from a real sequence acquired during the execution of the algorithm.

Fig. 1. Sequences of images of basic movements

3. Vergence

The vergence is one of the basic ocular movements. The main objective is to keep the target of interest centred in the visual field while the target is moving in depth. To perform this pursuit the eyes make a rotation movement of both eyes of the same magnitude but in opposed direction.

Therefore, for this movement the oculomotor system controls the angle between the optic axes, and it is called the vergence angle, w, see figure 2(a). The control is made in such a way that a fixation point along some specified gaze direction is kept at the centre of the visual field.

Given that, the vergence angle is directly related to target distance, the visual cues related with depth can be used to help the vergence system. The algorithm proposes to use disparity as the visual cue for to the vergence control system.

In active vision the problem disparity calculation is treated from different points of view: cepstral filter [8], phase correlation 191 and normalised cross-correlation (NCC) [10], [11].

The vergence control system proposed is based on the NCC.

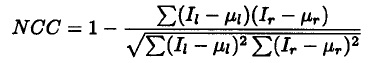
assuming that the vergence movement produce a rotation of both eyes of the same magnitude but in opposed direction, this mean that the target is located symmetrically with respect to the centre of each image (see figure 2(b)). The algorithm selects a sub-image, over the left epipolar band, and computes the NCC with the symmetrical sub-image in the right epipolar band. This pair of sub-images are taken along the epipolar band. At the end of this step we get a symmetrical correlation index (see also figure 2(b)). All the minima of this index that surpass a fixed value, give us information about possible targets. As it can be seen, there is a set of minima that are very close to the main minimum. In order to assure the correct choose, the proposed algorithm makes a second NCC between the sub-images corresponding to each minimum and the sub-image acquired in the previous stage (t - 1)^2. In figure l(b) we can see a sequence of images extracted form a real execution of the algorithm.

Fig. 2. Vergence Control System

4. Smooth Pursuit

The smooth pursuit is one of the basic ocular movements. The main objective is to keep the target of interest centred in the visual field when the target is moving laterally. This produce a rotation of both eyes of the same magnitude and in the same direction.

In a first approach, the solution can be seen as a monocular stabilisation problem. Solving the problem for each camera the problem of smooth pursuit is also solved. Even though, the solution is correct, it does not take advantage of all the possibilities of the binocular head.

One way to measure the degree of binocular displacement, also called version, can be made from two angles called pan, p, and tilt, 7, which correspond to the gaze azimuth and elevation of the fixation system. Figure 2(a) shows this geometry in the case of 7 = 0, that is, on the vergence plane. These angles are directly related to the target slip and all the visual cues related with movement detection can be used to design the version system. The proposed algorithm uses the positional error as the input of the system.

The version control system presented is based on NCC and on the permanent vergence hypothesis. This hypothesis is based on the immediate compensation of the vergence error, therefore, version algorithm works with images where the target is located in the same position in both images, t at is, the target has null.

The hypothesis of permanent vergence let us to define a new image that is the mean of left and right image, and is called cyclop image: disparity.

The version algorithm begins with the application of the NCC over a sub-image centred in the middle of the cyclop image taken in step t - 1, and a search image, twice times bigger than the size of the template pattern, centred arround the middle of the current cyclop image, taken in step t. The amount of movement is found when the best match is found and thereby the best estimate of movement during that cycle is achieved.

In figure l(c) we can see a sequence, of images extracted form a real execution of the algorithm.

5. Saccade

The saccade movement is the last basic movement that we have to studied. Saccade are point to point ballistic movements of the eyes produced by the need of fixing on a new target over the center of the image. The stimuli associated to this change are all the cues related with the attentional mechanism (colour, texture, geometric structure, speed, sounds, etc).

The ballistic character of saccades refers to the fact that they are not image driven, i.e. their trajectory is not affected by the image during the motion. As point to point movements they are purely position controlled and require exact position of the target beforehand. This movement is suddenly rotacional movements of both eyes with the same magnitude and direction. In this sense, it is very similar to the smooth pursuit, but in the saccade system the positional error is pre-calculated by the attentional mechanism.

6. Gaze Control

In the processing stage the acquired images need to be kept relatively stable on the retina so that visual processing may be carried out. If the image slips across the retina, the receptors loose the ability to resolve the vision problems because of blur. Thus, the control problem of the eyes movement is inherent in active vision, and is considered one of the most important [12], [8]. The gaze control centres its work in one hand in the visual feedback &om the camerak and in the other in the control loop around the feedback. The problem of gaze control can be divided in two gaze movements: to hold an image stable on the retina, and to move the eye to look at new position in the space. These have\been referred as holding and shifiing movements in [13].'Each movement has a specific task in the visual perception and shows a modular structure that builds the ohomotor system. The gaze holding involves maintaining fixation on moving objects from a moving gaze platform, The gaze shifting transfers fixation rapidly from one yisual target to another. The general distinction between these two movements is based on the speed, amplitude and the inter-ocular co-operation of the basic movements.

6.1. Gaze Holding

In this section we present the visuomotor behaviour that implement the holding system, also called binocular tracking. This behaviour is composed by focus and vergence to get depth information about the target movement and smooth pursuit to get lateral displacement. The co-ordination is based in a parallel scheme with three behaviours running at the same time. This scheme is broken when the hypothesis of permanent vergence is no longer guarantee. In this situation the output of the version process does not have correct input and the positional error estimation can not be extracted. The vergence behaviour inhibits3 the pursuit behaviour. The scheme of this algorithm can be seen in figure 3(a).

The gaze shifting is the ballistic change to a new point in the three-dimensional scene. This behaviour needs three basic movements, focus and vergence for depth information and saccade for lateral displacement. The co-ordination follows a sequential schema. First of all, a saccade movement is performed, that movement is ordered by an attentional process.

After this movement, the system has a new visual scenario, the eye that had visible the new target point of fixation, now it has the object centred in the middle of the image. The other eye needs to make a movement of vergence that is driven by the focus system The focus algorithm gives to the system the information about depth, and thus limit the search area for the vergence movement. In figures 3(a) and 4 we can see the co-ordination scheme and the graphical sequence of the algorithm steps.

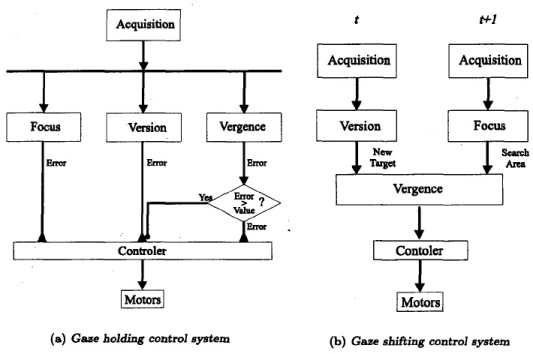
Fig. 3. Gaze control scemes

6.2. Gaze Shifting

After this movement, the system has a new visual scenario, the eye that had visible the new target point of fixation, now it has the object centred in the middle of the image. The other eye needs to make a movement of vergence that is driven by the focus system. The focus algorithm gives to the system the information about depth, and thus limit the search area for the vergence movement. In figures 3(a) and 4 we can see the co-ordination scheme and the graphical sequence of the algorithm steps.

7. Experiments

In this section we show the results of some experiments on the presented gaze control algorithms. The system runs in a Pentium-166 over a mobile platform called Gidebot [14].

The mobile platform use the parameters of the gaze control algorithms to decide the movements to be done. The experiments are directed to implement some visual tasks:

Time-to-contact (figure 5): the system selects a target and moves ahead the platform until the vergence angle is bigger than a value of security. If pan angle has a deviation bigger than a fixed value the system turn to left or to right to straight again.
Following moving objects (figure 6): the gaze control parameters are used as in previous task. Now, if the vergence is bigger than the security value the mobile platform remains stopped, if vergence angle is smaller than the security value the platform moves ahead.
Obstacle avoidance (figure 7): the system selects a target and moves ahead until the security distance, then, it turns around taken the fixation point as a centre of the avoidance movement, i.e. the system have to maintain the vergence angle fixed while the platform turns and advances to avoid the obstacle.

Fig. 4. Gaze control scemes

8. Concluding Remarks

We have presented two visual behaviours, gaze holding and gaze shifting, for head-eye systems. The gaze control is built from a set of basic movements. The systems proposed in this work for the basic movements is based on the simplicity of the algorithms and in the fact that the use of a feedback control architecture compensates low precision errors. This design let rise a behaviour with a high level of confidence.

These behaviours have been used for solving a set of relevant problems for autonomous system as time-to-contact, following a moving objects and obstacle avoidance strategy. These algorithms use information of the state of the head system, i.e. vergence angle, pan and tilt of the mount, to decide the next movement of the mobile platform.

Working example of diferent visual tasks. Sequence a following moving objects

Fig. 7. worm exmple of diferent visu& tasks. Sequence of a obstacle avoidance

References

D. Marr, Vision, W.H. Freeman, San Francisco, CA, 1982.
R. Bajcsy, “Active perception vs. passive perception,” in Proceedings Third IEEE Workshop on Computer Vision, Bellair, MI, October 1985, pp. 55-59.
Y. Aloimonos, I. Weiss, and A. Bandyopadhyay, “Active vision,” in Proceedings 1st International Conference of Computer Vision (ICCV), London, June 1987, pp. 35-54.
D. Ballard, “Animate vision,” in Procedeeins of the International Join Conference on Artificial Intelligence AAAI, Detroit, 1989.
X. Roca, X. Binefa, and J. VitriB, “New autofocus algorithm for cytological tissue in a microscopy environment,” Optical Engineering, vol. 37, no. 2, pp. 635-641, February 1998.
X. Binefa and J. VitriB, “A contrast-based focusing criterium,” in 13th International Conference of Pattern Recognition, Vienna (Austria), 1996, pp. 805-809.
E.P. Krotkov, Active Computer Vision by Cooperative Focus and Stereo, Springer-Verlag, New-York, 1989
D.J. Coombs, ReaLTime Gaze Holding in Binocular Robot Viaion, Ph.D. thesis, University of Rochester, June 1992.
A. Maki and T. Uhlin, “Disparity selection in binocular pursuit,” Tech. Rep. ISRN KTH/NA/P-95/17-SE, Royal Institute of Technology. Computational Vision and Active Perception Laboratory, September 1995
K. Pahlavan, Active Robot Vision and Primary Ocular Processes, Ph.D. thesis, Royal Institute of Technology. Computational Vision and Active Perception Laboratory, 1993.
A. Bernardino, “Seguimento binocular de alvos mbveisbaseado em imagens log-polar,” M.S. thesis, Instituto Superior Tbcnico, Lisbon, Portugal, January 1997.
M.J. Swain and M.A. Stricker, i‘Promising directions in active vision,” International Jurnal of Computer Vision, vol. 11, pp. 109-126, 1993
R.H.S. Carpenter, The Eye Movements, Pion Limited, London, 1988.
X. Roca, Processos Oculars Bbics: Zmplementacid i Integmcid. Aplicacid a1 Control de la Marada en Temps Real, Ph.D. thesis, Universitat Autbnoma de Barcelona, June 1998.