Источник: Министерство образования Российской Федерации. Нижегородский государственный университет им. Н.И. Лобачевского. Учебное пособие. Издание 2-е, дополненное. Издательство Нижегородского госуниверситета. Нижний Новгород. 2003 г.

Настоящий текст посвящен изложению теоретических основ приближенных методов решения обыкновенных дифференциальных уравнений. Он написан на основе курса лекций, которые автор читал в 1991 – 96 гг. на механико-математическом факультете Новосибирского государственного университета.

Здесь представлены одно- и многошаговые методы решения задачи Коши, описаны понятия аппроксимации, устойчивости и сходимости разностных схем, приведены признаки сходимости, изложены методы решения жестких уравнений. Для краевых задач описаны методы стрельбы, конечно-разностные и проекционные методы решения. Кроме того, в третьей главе совсем кратко описаны приближенные методы решения интегральных уравнений. Основное внимание уделяется идейной стороне вопроса, конкретные методы решения описываются лишь как иллюстративный материал, очень мало обсуждаются алгоритмические вопросы. Как правило, мы старались обращать внимание на геометрическую, а не на аналитическую суть описываемых методов.

§ 1.1. Сведения из теории обыкновенных дифференциальных уравнений. Постановки задач

В этом параграфе кратко напоминаются основные сведения из теории обыкновенных дифференциальных уравнений, описываются возможные методы приближенного решения задачи Коши и постановка задачи о разностных методах решения задачи Коши.

1.1.1. Воспоминания о курсе "Обыкновенные дифференциальные уравнения"

Если не оговорено противное, мы будем рассматривать систему обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно старшей производной, т. е. систему вида

x′ = f(t, x),

(E)

где f: R×R^m → R^m — непрерывная функция.

На протяжении всего курса R^m — m-мерное линейное вещественное пространство. Мы всегда считаем, что в R^m фиксирован базис и отождествляем R^m с координатным m-мерным вещественным пространством: точки из R^m — это упорядоченные наборы m вещественных чисел x = (x₁, ..., x_m). Таким образом, (E) — это сокращенная форма записи системы дифференциальных уравнений

x′1= f1(t, x1, ..., xm),

...

x′m= fm(t, x1, ..., xm),

в которой x = (x₁, ..., x_m), а f(t, x) = (f₁(t, x), ..., f_m(t, x)) = (f₁(t, x₁, ..., x_m), ..., f_m(t, x₁, ..., x_m)). Кроме того, предполагается, что в R^m фиксирована некоторая норма || · ||.

Решением уравнения (E) на промежутке [a, b] называется функция φ: [a, b] → R^m, обращающая (E) в тождество на [a, b]:

φ′(t) ≡ f(t, φ(t)),   t ∈ [a, b].

График решения (лежащий, по определению, в расширенном фазовом пространстве R×R^m) называется интегральной кривой I_φ. Проекция интегральной кривой на фазовое пространство R^m параллельно R называется траекторией T_φ. Здесь же отметим, что независимую переменную t мы в первой главе всегда будем трактовать как время.

В общей ситуации, уравнение (E) имеет бесконечное множество решений (точнее, m-параметрическое семейство решений). Для того чтобы выделить одно из них, нужны дополнительные условия (уравнения). Такие условия могут быть различными. В этой главе рассматривается только один вид дополнительных условий, так называемые начальные условия — требование, чтобы решение в заданной точке принимало заданное значение:

x(t0) = x0.

(C)

Задача о нахождении решения уравнения (E), удовлетворяющего начальному условию (C), называется задачей Коши. Обозначение "задача Коши (E) – (C)" будет универсальным, т.е. действовать на протяжении всей книги; универсальные обозначения и предположения будут заключаться в рамку:

Задача Коши (E) – (C).

Говорят, что функция f удовлетворяет условию Липшица по второму аргументу, если

∃(L) ∀(t ∈ R; x, y ∈ Rm) [||f(t, x) – f(t, y)|| ≤ L||x – y||]

(число L называется константой Липшица).

Фундаментальное в теории обыкновенных дифференциальных уравнений утверждение о разрешимости задачи Коши — следующая

Теорема Коши — Пикара. Если функция f непрерывна по первому аргументу и удовлетворяет условию Липшица по второму, то задача Коши (E) – (C) на любом отрезке вида [t₀, t₀ + T] имеет единственное решение.

Всюду ниже мы всегда будем предполагать, что

выполнены условия теоремы Коши — Пикара. При этом обозначение L для константы Липшица будет универсальным.

Простым достаточным условием выполнения условия Липшица является следующее утверждение. Если функция f дифференцируема по второму аргументу и ее производная равномерно ограничена некоторой константой L: ||∂f(t, x)/∂x|| ≤ L при всех (t, x) ∈ R×R^m, то она удовлетворяет условию Липшица с константой L.

Это же утверждение в "координатной форме": если функции (t, x) → f_i(t, x) = f_i(t, x₁, ..., x_m) дифференцируемы по последним m аргументам и все частные производные ограничены некоторой константой K: |∂f_i(t, x₁, ..., x_m)/∂x_j| ≤ K при всех (t, x₁, ..., x_m) ∈ R×R^m и i, j = 1, ..., m, то функция f удовлетворяет условию Липшица с некоторой константой L. (Найдите L через K и m.)

Несколько слов о геометрической трактовке уравнения (E). В каждой точке расширенного фазового пространства это уравнение задает направление касательной к интегральной кривой, поскольку предписывает, чему должна равняться производная φ′(t) в точке (t, x) = (t, φ(t)). Если в каждой точке R×R^m вектором (1, f(t, x)) указать направление касательной, то получившийся объект называют полем направлений, отвечающим уравнению (E)

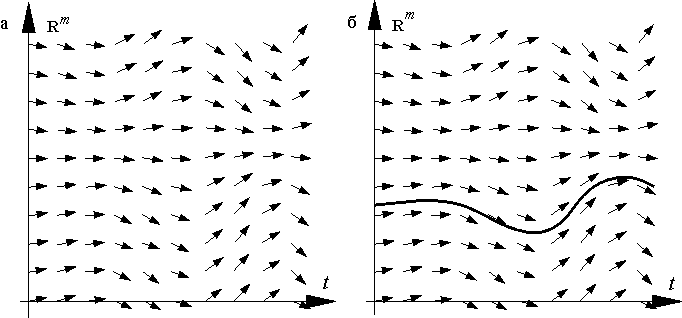
Рисунок 1 — Поле направлений и интегральные кривые

(рис. 1, а). Интегральная кривая должна "касаться" векторного поля в каждой своей точке (рис. 1, б). Поэтому расширенное фазовое пространство можно представлять как парк, часто заполненный стрелками-указателями, а решение — как прогулку по этому парку в соответствии со стрелками (в направлении, указываемом стрелками).

Утверждение о гладкости решений. Если в задаче (E) – (C) функция f является k раз непрерывно дифференцируемой, то ее решение φ непрерывно дифференцируемо k + 1 раз.

1.1.2. Для чего нужны дифференциальные уравнения и чего мы от них хотим?

Дифференциальные уравнения являются инструментом познания мира и, как всякий инструмент, они развиваются и самосовершенствуются. Поэтому с точки зрения теории это самодостаточный объект. С прикладной же точки зрения дифференциальные уравнения описывают окружающий нас мир, и с их помощью мы можем узнавать о нем новое. "Познание мира" с помощью дифференциальных уравнений обычно состоит из двух этапов: составление модели (дифференциального уравнения, описывающего то или иное явление) и исследование получившейся модели.

Нас интересует в данном курсе второй этап. Поскольку именно решения описывают те или иные природные процессы, в конечном счете прикладнику важна информация именно о них. Большáя часть теории обыкновенных дифференциальных уравнений посвящена изучению решений в случаях, когда оно точно не известно. Это так называемая качественная теория обыкновенных дифференциальных уравнений. К ней относится, например, теория устойчивости, позволяющая, не зная решения, по свойствам уравнения указать свойства устойчивости решений. В конкретных задачах часто возникает необходимость найти решение или иметь возможность вычислить решение в каждой точке. Иногда решение некоторых дифференциальных уравнений удается выписать в явном виде. В то же время множество дифференциальных уравнений, решения которых можно в явном виде выразить через элементарные функции, весьма и весьма бедное. Уже простейшее нелинейное уравнение первого порядка x′ = t² + x² не допускает решений в квадратурах. Поэтому нужны методы, позволяющие вычислять решения произвольных дифференциальных уравнений приближенно.

1.1.3. Как можно решать дифференциальные уравнения приближенно? Метод разложения в ряды.

Исторически первым методом решения дифференциальных уравнений, который использовал еще их автор Ньютон, был метод разложения в ряды. Искомое решение разлагается в ряд (например, Тейлора) с неизвестными коэффициентами. Этот ряд подставляется в (E) и из получившегося уравнения находятся коэффициенты.

Предположим, например, что в уравнении (E) функция f аналитична, т.е. допускает разложение в ряд по степеням t и x:

f(t, x) = f00 + f10t + f01x + f20t2 + f11tx+ f02x2 + ... .

(1)

Тогда известно (это достаточно громоздко доказываемая теорема), что решение φ задачи (E) – (C) также аналитично, т.е. представимо в виде ряда

φ(t) = x0 + x1t + x2t2 + ...

(2)

с неизвестными пока коэффициентами x₀, x₁, .... Очевидно,

φ′(t) = x1 + 2x2t + 3x3t2 + ... .

(2)

Подставим разложения (1) – (3) в уравнение (E) и в получившемся уравнении приравняем коэффициенты при одинаковых степенях t. Кроме того, подставим разложение (2) в начальное условие (для простоты, будем считать, что t₀ = 0). Получим бесконечную систему уравнений

x0 = x0, x1 = f00 + f01x0 + f02x20+ ..., 2x2 = f10 + f01x1 + f11x0 + 2f02x0x1 + ..., 3x3 = f20 + f11x1 + f01x2 + f02x21+ 2f02x0x1 + ..., . . .

Из второго уравнения находится x₁ (через x₀ и f_ij), из третьего — x₂ (через x₀, x₁ и f_ij) и т. д. Таким способом могут быть найдены все коэффициенты в разложении (2). Частичные суммы ряда (2) аппроксимируют решение с заданной точностью.

Задача 1.1.1. Найдите описанным методом решение скалярной задачи Коши x′ = ax, x(t₀) = x⁰.

Эти методы требуют, как правило, большого объема аналитической плохо алгоритмизируемой работы. Например, для нахождения коэффициентов ряда Тейлора решения нужно вычислять производные высоких порядков от правой части уравнения. В силу этого разложения решений в такие ряды пока мало пригодны для практического использования на ЭВМ. Кроме того, эти методы обладают плохими свойствами устойчивости в вычислительном плане.

1.1.4. Как можно решать дифференциальные уравнения приближенно? Метод последовательных приближений.

Для отыскания приближенного решения можно воспользоваться также методом последовательных приближений. Напомним его суть. Задача Коши (E) – (C) эквивалентна интегральному уравнению

x(t) = x0 + ∫ t t0 f[s, x(s)]ds,   t ∈ [t0, t0 + T]

(4)

в следующем смысле: если φ — решение задачи Коши (E) – (C), то φ удовлетворяет уравнению (4) и наоборот.

Обозначим правую часть уравнения (4) через (Jx)(t). Тогда оно перепишется в операторном виде

x = Jx.

Если применить к получившемуся уравнению метод простой итерации, начиная, например, с функции x⁰(t) ≡ x⁰, то получим рекуррентно определяемую последовательность функций:

xn(t) = Jxn–1 = x0 + ∫ t t0 f[s, xn–1(s)]ds,    n = 1, 2, ... .

(5)

Известно, что последовательность функций xⁿ равномерно сходится к решению задачи (E) – (C), причем известна оценка скорости сходимости. Если теперь заменить в (5) интеграл (вовсе не обязательно берущийся) какой-либо квадратурной формулой (возможность такой замены требует, конечно, обоснования), то получится метод, позволяющий вычислять все более и более точные приближения решения.

Задача 1.1.2. Найдите описанным методом решение скалярной задачи Коши x′ = ax, x(t₀) = x⁰.

Поскольку этот метод требует большого объема вычислительной работы (на каждой итерации приходится неоднократно вычислять значения правой части уравнения), он играет, в основном, теоретическую роль - например, он полезен при доказательстве теоремы Коши — Пикара или при доказательстве утверждений о дифференцируемости решений по параметру или начальным данным.

1.1.5. Как можно решать дифференциальные уравнения приближенно? Асимптотические методы.

Искать приближенные решения можно также, пытаясь найти интегрируемое в квадратурах дифференциальное уравнение, решения которого аппроксимируют решения исходного. Такое уравнение указать, как правило, все-таки трудно. Поэтому можно попытаться искать более простое уравнение, аппроксимирующее решения исходного. С этим направлением тесно связаны асимптотические методы или методы разложения по параметру. В данном курсе мы их тоже не рассматриваем.

В настоящее время наиболее универсальными и эффективными методами приближенного решения дифференциальных уравнений признаны так называемые конечно-разностные (их еще называют разностными или сеточными) методы.

1.1.6. Конечно-разностные методы. Постановка задачи.

Пусть для любого τ > 0 задано множество G_τ точек t₀ < t₁ < ... < t_n = t₀ + T отрезка [t₀, t₀ + T] такое, что τ = max_{0≤i≤ n}{t_i+1 – t_i}. Множество G_τ называется сеткой, его элементы — узлами, а числа τ_i = t_i+1 – t_i — шагами сетки. Если τ_i ≡ τ = T/n, то говорят о сетке с постоянным шагом, или сетке с шагом τ, или равномерной сетке.

Конечно-разностным или разностным методом приближенного решения задачи (E) – (C) называют любые методы (приемы, способы), позволяющие для каждого τ > 0 указать φτ: Gτ → Rm (такие функции называют сеточными), которая в том или ином смысле аппроксимирует решение φ задачи (E) – (C). Разумеется, возникает вопрос: в каком смысле понимать фразу "сеточная функция аппроксимирует решение"? Поскольку φτ и φ принадлежат разным пространствам, то естественно изометрично вложить пространство сеточных решений и пространство решений в одно пространство, и уже в этом пространстве измерять расстояние между ними. Например, вложить пространство сеточных функций в пространство непрерывных функций, заменив сеточную функцию φτ ломаной φτ, и считать, что φτ хорошо аппроксимирует φ, если ||φτ – φ||C ≝ max{||φτ(t) – φ(t)||Rm: t ∈ [t0, t0 + T]} мала.

Чаще поступают следующим образом. "Проектируют" решение φ на пространство сеточных функций S_τ, ставя в соответствие функции φ ее сужение P_τφ на сетку G_τ. На пространстве сеточных функций S_τ задают норму, обычно, либо равномерную: ||y|| = max_t∈Gτ{|| y(t)||}, либо вадратичную: ||y|| = (∑_t∈Gτ || y(t)||²)^1/2. Теперь можно считать, что φ_τ хорошо аппроксимирует φ, если ||φ_τ –P_τφ||_Sτ мала.

Всюду ниже мы будем считать, что на пространстве Sτ задана равномерная норма и будем обозначать эту норму через || · ||τ.

Если x — сеточная функция на Gτ, то ее значение в точке ti мы всегда будем обозначать через xi, а не стандартно x(ti).

Pτφ для любой функции φ на отрезке [t0, t0 + T] всегда обозначает сужение φ функции на сетку Gτ: [Pτφ]i = [Pτφ](ti) = φ(ti).

В данном параграфе на примере явного метода Эйлера даются основные понятия теории разностных схем — понятия сходимости, аппроксимации и устойчивости. Доказывается теорема Лакса. Описываются основные приемы построения разностных схем.

1.2.1. Метод ломаных Эйлера.

Напомним, что метод ломаных Эйлера – это метод нахождения аппроксимирующей интегральную кривую ломаной, который в образах парка со стрелками-указателями может быть представлен так (рис. 2). Из точки (t₀, x₀) = (t₀, x⁰) расширенного фазового пространства движемся τ "секунд", сообразуясь со стрелкой, помещенной в этой точке, и не обращая внимания на остальные стрелки. Придя (через время τ) в точку (t₁, x₁), меняем направление, пользуясь указанием, задаваемым стрелкой в точке (t₁, x₁); через τ секунд приходим в точку (t₂, x₂), опять меняем направление и  т. д. Полученная траектория и является ломаной Эйлера, аппроксимирующей решение задачи (E) – (C).

Рисунок 2 — Метод ломаных Эйлер

Легко видеть, что координаты i-й вершины (i = 1,..., n) ломаной Эйлера определяются формулами

ti = t0 + iτ,   x0 = x0,    xi = xi–1 + τf(ti–1, xi–1).

(1)

Перепишем эти равенства в следующем виде:

xi – xi–1 τ  – f(ti–1, xi–1) = 0,  если i = 1,..., n,

xi = x0, если i = 0.

1.2.2. Операторная запись задачи (E) – (C).

Запишем метод ломаных Эйлера в общем виде, в котором могут быть записаны другие разностные методы и который позволяет укладывать исследование таких методов в общую схему. Для этого сначала запишем задачу (E) – (C) в операторной форме. Начальное условие (C) можно записать в виде

g(x) = 0,

где функция g имеет вид g(x) = x(t₀) – x⁰. Тогда начальную задачу (E) – (C) можно записать в операторной форме

F(x) = 0,

(O)

где F(x) = (x′(·) – f(·, x), g(x)). Не будем обсуждать подробно вопрос об областях определения и значений оператора F. В случае задачи (E) – (C) можно считать, например, что областью определения D(F) оператора F служит пространство C¹([t₀, t₀ + T], R^m) непрерывно дифференцируемых на отрезке [t₀, t₀ + T] функций со значениями в R^m, а областью значений R(F) — декартово произведение C¹([t₀, t₀ + T], R^m)×R^m. Заметим, что решение φ задачи (E) – (C) есть прообраз нуля для оператора F: φ = F^–1(0).

1.2.3. Операторная форма метода ломаных Эйлера.

Пусть x — сеточная функция из S_τ. Определим на S_τ оператор F_τ равенством

[Fτ(x)]i = { xi – xi–1 τ   –  f(ti–1, xi–1),  если i = 1, ..., n, xi – x0,  если i = 0;

(2)

(Здесь [F_τ(x)]_i обозначает значение сеточной функции [F_τ(x)] в точке t_i.)

Задача о нахождении ломаной Эйлера, очевидно, эквивалентна задаче о нахождении решения φ_τ уравнения

Fτ(x) = 0

(S)

в пространстве Sτ сеточных функций в следующем смысле: значения (φτ)i решения уравнения (S) в узлах сетки и только они являются ординатами вершин ломаной Эйлера в точках ti (см. формулу (1)). Таким образом, вместо точного решения φ = F–1(0) мы ищем приближенное решение φτ = Fτ–1(0).

1.2.4. Разностные схемы.

Любое уравнение вида (S) для нахождения сеточной функции x будем называть разностной схемой, а его (уравнения) решение, которое мы всегда будем обозначать φ_τ, — разностным или сеточным решением (уравнения (S)). Оператор F_τ будем называть разностным оператором. Разумеется, в таком общем виде определение разностной схемы никак не связано с исходной задачей Коши (E) – (C) (уравнением (O)). В то же время, если в (S) оператор F_τ определен формулой (2), то разностная схема (S) имеет к задаче (E) – (C) самое непосредственное отношение (объяснить, что означают эти слова, и есть цель остальной части параграфа).

В последнем случае разностная схема (S) называется явной (разностной) схемой Эйлера. Явной она называется потому, что ее решение может быть выписано в явном виде с помощью рекуррентных соотношений:

(φτ)0 = x0,

(φτ)i = (φτ)i–1 +τf[ti–1,(φτ)i–1],   i = 1, ..., n.

Единственное отличие метода ломаных Эйлера от явной схемы Эйлера заключается в том, что в первом ищется функция, заданная на отрезке [t₀, t₀ + T] (ломаная Эйлера), а во втором — на сетке G_τ (вершины этой ломаной).

Задача 1.2.1. Докажите, что разностное решение φ_τ явной схемы Эйлера для задачи Коши

x′ = ax,   x(t0) = x0

(a ∈ R) на равномерной сетке (τ_i = iτ) задается формулой (φ_τ)_i = x⁰(1 + τa)ⁱ.

1.2.5. Пример. Сходимость явной разностной схемы Эйлера.

В условиях задачи 1.2.1 разностное решение φ_τ аппроксимирует решение φ(t) = x⁰e^at интересующей нас исходной (дифференциальной) задачи в следующем смысле: при всех t ∈ [0, T]

(φτ)i→ x0eat при τ→ 0,

(3)

где i = [t/τ] (здесь [t/τ] — целая часть числа t/τ; ниже мы наряду с обозначением [a] для целой части числа a используем обозначение {a} для его дробной части: a = [a]+ {a}). Действительно,

lim τ→0 (φτ)i =  lim τ→0 x0(1 + τa)i = x0· lim τ→0 (1 + τa)[t/τ] =

= x0· lim τ→0 (1 + τa)t/τ–{t/τ} =

= x0· lim τ→0 (1 + τa)t/τ· lim τ→0 (1 + τa)–{t/τ}.

Сомножитель lim_τ→0(1 + τa)^–{t/τ} равен единице, поскольку {t/τ} ∈ (0, 1). Второй сомножитель также вычисляется тривиально:

lim τ→0 (1 + τa)t/τ =  lim τ→0 (1 + τa)[1/(τa)] ·at =  [ lim τ→0 (1 + τa)1/τa ] at  = eat

и соотношение (3) доказано.

Задача 1.2.2. Докажите более сильное, чем (3) утверждение

||φτ – Pτφ||τ→ 0 при τ→ 0.

означающее, что предельное соотношение (3) выполнено равномерно по i ∈ {1, ..., n).

1.2.6. Сходимость разностных схем.

Будем говорить, что разностная схема (S) сходится (к решению φ задачи (E) – (C)), если

||φτ – Pτφ||τ→ 0 при τ→ 0.

(4)

Сходимость разностной схемы означает, что при достаточно малом τ значения сеточного (приближенного) решения φ_τ и точного решения φ мало отличаются. Соотношение (4) на практике оказывается мало полезным, поскольку на основании его нельзя судить о том насколько малым мы должны выбрать шаг τ, чтобы в узлах сетки точное и приближенное решения отличались друг от друга не более, чем на ε (заранее заданную точность). Если удается доказать, что при достаточно малых τ > 0

||φτ – Pτφ||τ ≤ Cτk,

(5)

где C — не зависящая от τ константа, то говорят, что схема (S) сходится с порядком k (или является схемой k-го порядка (сходимости)). Оценка (5), если в ней известна (для конкретной задачи (E) – (C)) константа C, позволяет по заранее выбранной точности ε a priori выбрать шаг так, чтобы приближенное решение аппроксимировало решение данной (дифференциальной) задачи Коши с точностью ε:

||φτ – Pτφ|| τ ≤ ε;

достаточно взять τ ≤ k√ε/C.

1.2.7 Аппроксимация.

Явная схема Эйлера обладает двумя важными свойствами, из которых, как будет показано ниже, последует ее сходимость с первым порядком. Во-первых, при достаточно малых τ

||Fτ(Pτφ)||τ ≤ Caτ,

(6)

где C_a — константа, не зависящая от τ, а φ — как обычно, точное решение задачи (E) – (C). В этом случае говорят, что схема (S) имеет первый порядок аппроксимации на решении. (Если в правой части неравенства (6) стоит C_aτ^k, то, соответственно, говорят о схеме k-го порядка аппроксимации (на решении).) Другими словами, неравенство (6) эквивалентно тому, что ||F_τ(P_τφ)||_τ = O(τ) (в случае схемы k-го порядка аппроксимации — O(τ^k)). Тот факт, что разностная схема обладает аппроксимацией на решении, означает, грубо говоря, что при подстановке точного решения дифференциальной задачи в разностную схему мы получаем невязку соответствующего порядка малости по τ. (Было бы идеально, если бы после такой подстановки мы получали в левой части нуль, однако в общем случае конструктивно такие схемы выписать нельзя.)

Часто вместо свойства аппроксимации на решении рассматривают формально более жесткое требование, которое называют свойством аппроксимации (в зарубежной литературе — согласованностью); именно, говорят, что схема (S) является схемой k-го порядка аппроксимации на функции x, если при достаточно малых τ

||Fτ(Pτx) – PτF(x)||τ ≤ Caτk.

Обычно требуется, чтобы схема обладала свойством аппроксимации на множестве функций из некоторого класса гладкости. Очевидно, если решения дифференциального уравнения (E) m раз непрерывно дифференцируемы, а разностная схема обладает k-м порядком аппроксимации (согласованности) на m раз непрерывно дифференцируемых функциях, то она обладает k-м порядком аппроксимации на решении.

1.2.8. Аппроксимация явной схемы Эйлера.

Покажем, что если функция f в (E) непрерывно дифференцируема по t и x, то явная схема Эйлера имеет первый порядок аппроксимации на решении. Действительно, пусть φ — решение задачи (E) – (C):

φ′(t) ≡ f[t, φ(t)],   t ∈ [t0, t0 + T].

Поскольку f дифференцируема по t и x, решение φ дважды непрерывно дифференцируемо (см. утверждение о гладкости решений). В частности, найдется M такое, что ||φ′′(t)|| ≤ M при всех t ∈ [t₀, t₀ + T]. Кроме того, в силу гладкости φ для любых t = 1, ..., n

φ(ti) = φ(ti–1 + τ) = φ(ti–1) +τφ′(ti–1) +  τ2 2 φ′′(ti–1 + Φiτ),

где Φ ∈ (0, 1). Но тогда

[Fτ(Pτφ)]i =  (Pτφ)i – (Pτφ)i–1 τ – f[ti–1, (Pτφ)i–1] =

=  φ(ti) – φ(ti–1) φ – f[ti–1, φ(ti–1)] =

=  φ(ti–1) + τφ′(ti–1) +  τ2 2 φ′′(ti–1 + Φiτ) – φ(ti–1) τ  –

– f[ti–1, φ(ti–1)] = φ′(ti–1) +  τ2 2 φ′′(ti–1 + Φiτ) – f[ti–1, φ(ti–1)] =

=  τ 2 φ′′(ti–1 + Φiτ).

(Если i = 0, то очевидно, [F_τ(P_τφ)]_i = 0.) Из сказанного следует, что

||Fτ(Pτφ)|| τ =  max 0≤i≤n ||[Fτ(Pτφ)]i|| ≤

≤  τ 2 max 0≤i≤n ||φ′′(ti–1+Φiτ)|| ≤ τ M 2 ≝ Caτ.

Задача 1.2.3. Покажите, что явная схема Эйлера обладает первым порядком аппроксимации (согласованности) на любой дважды непрерывно дифференцируемой функциию

1.2.9. Устойчивость.

Второе важное свойство, которым обладает явная схема Эйлера, называется устойчивостью и определяется так: если z ∈ S_τ и, кроме того, ||z||_τ и τ достаточно малы, то уравнение

Fτ(y) = z

(7)

однозначно разрешимо и существует такая не зависящая от τ и ||z||_τ константа C_s, что

||y – φτ||τ = ||Fτ–1(z)– φτ||τ ≤ Cs||z||τ.

(8)

Устойчивость разностной схемы означает, что малые возмущения z в начальных данных и правой части разностной схемы приводят к равномерно малому по τ изменению решения (напомним, что φτ — решение невозмущенной системы, а Fτ–1(z) — возмущенной). Поскольку φτ = Fτ–1(z),неравенство (8), переписанное в виде ||Fτ–1(z)– Fτ–1(0)||τ ≤ Cs||z|| τ, означает, в частности, непрерывность обратного к разностному оператору оператора Fτ–1в нуле.

Устойчивость — очень важное в приложениях свойство разностных схем. При практической реализации на ЭВМ разностных методов возникают, в частности, проблемы, связанные с невозможностью представления точных чисел в компьютере. В результате мы решаем не разностную схему (S), а несколько отличающееся от (S) уравнение. Все такие возмущения в разностной схеме, грубо говоря, можно "перенести в правую часть" и, таким образом, считать, что в ЭВМ ищется решение не разностной схемы (S), но решение возмущенного уравнения (7). Свойство устойчивости разностной схемы гарантирует близость при достаточно малых τ между точным (теоретическим) решением φτ разностной схемы и его практической реализацией Fτ–1(z)(где z — суммарный вектор возмущений). Источником возмущений служит не только невозможность точного представления данных в ЭВМ, но и неточность определения физических параметров модели, погрешность измерений и т.п.

1.2.10. Пример. Устойчивость явной схемы Эйлера.

Докажем, что явная схема Эйлера устойчива.

Разрешимость уравнения (7) для любых τ и z очевидным образом следует из того, что явная схема Эйлера является явной: значения yi решения y = Fτ–1(z) этого уравнения определяются рекуррентными формулами

y0 = x0 + z0,

yi = yi–1 + τf(ti–1, yi–1) + τzi,   i = 1, ..., n.

Обозначим y – φ_τ через ξ. Очевидно,

ξ0 = z0,

ξi = ξi–1 + τf(ti–1, yi–1) – τf[ti–1,(φτ)i–1] + τzi,   i = 1, ..., n.

Покажем теперь, что

||ξi|| ≤ (1 + τL)i· L + 1 L ||z||τ.

Для этого заметим сначала, что

||ξi|| = ||ξi–1 + τf(ti–1, yi–1) – τf[ti–1,(φτ)i–1] + τzi|| ≤

≤ ||ξi–1|| + τ||f(ti–1, yi–1) –f[ti–1,(φτ)i–1]|| + τ||zi|| ≤

≤ ||ξi–1|| + τL||yi–1 – (φτ)i–1|| + τ||z|| τ = (1 + τL)||ξi–1|| + τ||z|| τ.

Проведя такие оценки i раз, получим

||ξi|| ≤ (1 + τL)||ξi–1|| + τ||z|| τ ≤

≤ (1 + τL)[(1 + τL)||ξi–2|| +τ||z|| τ] + τ||z|| τ =

= (1 + τL)2||ξi–2|| + [(1 + τL) + 1]τ||z|| τ ≤ ...

... ≤ (1 +τL)i|| ξ0|| + [(1 + τL)i–1 + ... + (1 + τL) + 1]τ||z|| τ =

= (1 + τL)i|| ξ0|| +  (1 + τL)i – 1 (1 + τL) – 1 τ||z||τ ≤

≤ (1 + τL)i|| z|| τ +  (1 + τL)i– 1 L ||z|| τ =

=  (1 + τL)iL + (1+ τL)i – 1 L ||z||τ ≤ (1+τL)i· L + 1 L ||z||τ.

Воспользуемся теперь известным неравенством (1 + α)^1/α < e (напомним также, что τ = T/n):

(1 + τL)i ≤ (1 + τL)n = (1 + τL)[(TL)/(τL)] ≤ [(1 + τL)[ 1/(τL)]]TL < eTL.

Окончательно,

||Fτ–1z– φτ|| τ = ||y – φτ|| τ = ||ξ|| τ =  max 0≤i≤n ||ξi|| ≤

≤  max 0≤i≤n eTL·  L + 1 L ||z|| τ = eTL· L + 1 L ||z||τ ≝ Cs|| z|| τ.

Итак, явная схема Эйлера устойчива.

Покажем теперь, что из аппроксимации и устойчивости следует сходимость разностной схемы.

1.2.11. Теорема Лакса.

Любая устойчиваяA> разностная схема k-го порядка аппроксимации на решении является схемой k-го порядка сходимости.

Д о к а з а т е л ь с т в о.  Действительно, если разностная схема имеет k-й порядок аппроксимации на решении, то ||Fτ(Pτφ)||τ ≤ Caτk и поэтому, в частности, при малых τ мала и ||Fτ(Pτφ)||τ. Следовательно, в силу устойчивости, Fτ–1[Fτ(Pτφ)] существует и ||Fτ–1[Fτ(Pτφ)]– φτ||τ ≤ Cs||Fτ(Pτφ)||τ. Но тогда, очевидно,

||Pτφ– φτ|| τ = ||Fτ–1[Fτ(Pτφ)]– φτ||τ ≤

≤ Cs|| Fτ(Pτφ)|| τ ≤ CsCaτ ≝ Cτk.

что и требовалось доказать.

Эта теорема описывает наиболее распространенный способ доказательства сходимости разностных схем.

Задача 1.2.4. Приведите пример не сходящейся разностной схемы, обладающей своством аппроксимации.

1.2.12. Немного о методах построения разностных схем.

Явная схема Эйлера может быть построена, исходя из различных соображений. Каждый из описываемых ниже приемов порождает ряд обобщений явной схемы Эйлера и может иллюстрировать основные методы построения разностных схем. В дальнейшем эти методы будут рассматриваться подробнее.

Попытаемся, отталкиваясь от уравнения (E), заменить его приближенным в том или ином смысле уравнением так, чтобы в результате получилась разностная схема. Первая идея выглядит так. Заменим в уравнении

x′(t) = f[t, x(t)]

(9)

производную x′(t) в точке t_i–1 ее приближенным значением [x(t_i) – x(t_i–1]/τ, а правую часть — ее значением в этой точке. В результате получим приближенное уравнение

x(ti) – x(ti–1) τ ≈ f[ti–1, x(ti–1)]

для отыскания значений точного решения уравнения (E) в точках сетки G_τ. Переход к сеточным функциям и замена приближенного равенства точным приводит к точному уравнению для приближенных значений решения, а именно, к явной схеме Эйлера. Использование других аппроксимаций производной в (9) (например, x′(t_i–1) ≈ [x(t_i+1) – x(t_i–1)]/2τ, а также других аппроксимаций правой части (например, f[t_i, x(t_i)]) взамен f[t_i–1, x(t_i–1)] позволяет получать другие разностные схемы.

Вторая идея основывается на замене дифференциального уравнения (9) интегральным

x(t + τ) = x(t) +  ∫ t+τ t f[s, x(s)]ds,

(10)

Если заменить в (10) t на t_i–1, а интеграл — приближенной квадратурной формулой (в данном случае прямоугольников), то мы получим приближенное уравнение

x(ti) ≈ x(ti–1) + τf[ti–1, x(ti–1)],

которое так же, как и выше приводит к явной схеме Эйлера. Если использовать другие квадратурные формулы (заменяя, например, интеграл на τf[t_i, x(t_i)] или τ[f(t_i–1, x(t_i–1)) + f(t_i, x(t_i))]/2), то будут получаться другие разностные схемы.

Третья возможность построения разностных схем связана с разложением решения в ряд Тейлора:

x(ti) = x(ti–1) + τx′(ti–1) +  τ2 2 x′′(ti–1) + ... .

"Обрежем" этот ряд до второго члена и выразим производную x′(t_i–1) из (9). В результате получим все то же приближенное уравнение

x(ti) ≈ x(ti–1) + τf[ti–1, x(ti–1)],

приводящее к явной схеме Эйлера. Удлинение отрезка ряда и другие аппроксимации коэффициентов приводят к другим разностным схемам.

Наконец, четвертая возможность связана с поиском решения в виде полинома. Допустим, мы ищем решение в виде полинома первого порядка:

ψ(t) = xi–1 + a·(t – ti–1)

с неизвестным коэффициентом a. Потребуем, чтобы этот полином точно удовлетворял уравнению (9) в некоторой точке t_i–1 + α:

ψ′(ti–1 + α) = a = f(ti–1 +α, xi–1 + aα).

Переходя к сеточным функциям, как и выше, получаем разностную схему:

xi = ψ(ti) = ψ(ti–1 + τ) = xi–1 + τf(ti–1 + α, xi–1 + aα).

При α = 0 это явная схема Эйлера. Если выбирать отличные от нуля α, а также брать полиномы более высоких порядков, то получается класс различных разностных схем.

Сопровождающие изложение задачи носят учебный характер, причем некоторые из них являются неотъемлемой частью излагаемой теории, и их результаты используются в последующем изложении.

Предисловие
Глава 1. Задача Коши
	§ 1.1. Сведения из теории обыкновенных дифференциальных уравнений. Постановки задач
	§ 1.2. Разностные схемы, сходимость, устойчивость
	§ 1.3. Методы Рунге — Кутты
	§ 1.4. О сходимости явных методов
	§ 1.5. Анализ погрешностей
	§ 1.6. Многошаговые методы
	§ 1.7. Устойчивость разностных схем
	§ 1.8. Жесткие системы
Глава 2. Краевая задача
	§ 2.1. Простейшие краевые задачи
	§ 2.2. Методы стрельбы
	§ 2.3. Конечно-разностные методы
	§ 2.4. Проекционные методы
	§ 2.5. Сходимость проекционных методов для линейных уравнений
Глава 3. Интегральные уравнения
	§ 3.1. Основные понятия теории интегральных уравнений
	§ 3.2. Приближенные методы решения интегральных уравнений II рода
Литература
Предметный указатель

Автор благодарен своему коллеге и товарищу

Анатолию Георгиевичу Слепцову

 за внимательное прочтение рукописи, полезные обсуждения, замечания и советы.