Назад в библиотеку

Сравнение мер расстояния в эволюционной сегментации временных рядов

Авторы: Jingwen Yu, Jian Yin, Jun Zhang

Перевод: Е.С. Шагаева

Источник (англ.): Comparison of Distance Measures in Evolutionary Time Series Segmentation

Аннотация: Сегментация является основным этапом в процессе анализа и исследования временных рядов. Учитывая набор шаблонов проектирования, эволюционное вычисление является подходящим инструментом для сегментации временных рядов, гибким и эффективным.

Предисловие

Сегментация временных рядов является основным этапом в процессе анализа и исследования временных рядов. Учитывая набор шаблонов проектирования, эволюционное вычисление является подходящим инструментом для сегментации временных рядов, гибким и эффективным. Однако, выбор мер расстояний в фитнесс-функции является очень важным этапом для эволюционной сегментации временных рядов, так как значительно влияет на сходимость алгоритма. В качестве подхода, используется прямой метод точка-точка (DPPD), он всегда используется в качестве меры подобия. Тем не менее, это хрупкие по времени жизни фазы. В этой статье будут представлены три другие меры расстояния для оценки фитнес-функций, которые основываются на замкнутых областях, времени и деформации тенденция подобия соответственно. Более того, эксперименты проводятся для сравнения производительности новых мер расстояния с DPPD подходом. Результаты показывают, что новое новые подходы к измерению величины расстояния превосходит DPPD-подход в точности сегментации.

Введение

Недавно, увеличивающееся использование временных данных стало толчком для различного рода научно-исследовательских работ в области сбора данных. Временные ряды - основные источники временных баз данных и могут быть легко получены из финансовых и научных приложений. Исследование временных рядов имеет фундаментальное значение [1]. Данные о временном ряде характеризуются их числовой и непрерывной природой, а также трудностью их обработки. Следовательно, есть потребность в дискретизации непрерывного временного ряда на значимые символы [2, 3]. Этот процесс назван "числовым-к-символическому" преобразованием (N/S) и рассматривается как один из большинства основных процессов перед исследованием временных рядов.

В работе [2] используется подход с фиксированной длиной окна сегмента временного ряда и представляет его со сформированными простыми образцами. Некоторые другие подходы в работах [4, 5] предлагают делить временной ряд с определенными точками перехода и представлять сегменты с соответствующими функциями. Чтобы найти циклическую периодичность во временном ряде, в работах [6, 7] используются методы сбора данных с сегментационной периодичностью.

В работах [1, 8], авторы рассмотрели проблемы нахождения подходящих моментов времени для сегментации ряда, когда шаблонов ряда-образца задан. Эту проблему рассматривают, как проблему оптимизации и она может быть решена с помощью эволюционных вычислений по выявлению важных моментов непосредственно из временных интервалов. В работе [1] использует прямое двухточечное (точка-точка) расстояние (DPPD) как мера подобия оценки фитнес-функции. Однако, DPPD не является подходящим методом, когда у двух последовательностей различная длина.

В этой статье отображено расширение к работе, представленной по ссылке [1], и рассматривается ограничение меры по расстоянию, основанной на DPPD. Представляются три другие меры по расстоянию для эволюционной сегментации временного ряда. Остальная часть статьи организована следующим образом: во втором разделе рассмотрены важные моменты в измерении и анализе меры расстояний, рассмотрены основные проблемы этих мер по расстоянию в DPPD для сегментации временного ряда. В третьем разделе, подробно обсуждаются три предложенные меры расстояния. В четвертом разделе представлены результаты эксперимента сравнения предложенного расстояния меры с оригинальными, представленными в работе [1]. В пятом разделе приводятся выводы по данной работе.

Обзор мер расстояния в эволюционной сегментации временных рядов

В этом разделе кратко рассматривается и анализируется подход DPPD.

2.1. Определение восприятия важных пунктов

При анализе временных рядов, часто встречающиеся образцы обычно могут быть абстрактно представлены несколькими критическими точками. Эти пункты имеют перцепционно важное влияние в человеческом видении. Основанный на этой идее, подход DPPD, использующий важные моменты (PIPs), чтобы охарактеризовать временную последовательность, в то время как последовательность запросов задана. Псевдокод процесса идентификации PIP приводится ниже:

  function FindPIP (P,Q) 
  Input: sequence P[1,...,m], length 
    of pattern Q[1,...,n] 
  Output: pattern SP[1,...,n], which 
    are the PIPs of sequence P. 
    Begin 
      First set SP[1] := P[1] and 
      SP[n] := P[m] 
      Repeat 
        Select point p[j] with highest 
        fluctuation rate to the adjacent 
        points in SP and add p[j] to SP 
        until all the PIPs of P are found, 
      i.e. SP[I,...,n] is fully filled 
        return SP 
    end.

2.2. Измерение расстояния

После определения PIPs, расстояние межвременной последовательности P и запрашиваемой последовательности Q, которые обе представляют из себя ряд PIPs, может быть вычислено непосредственно с помощью point-to-point (токчка-точка) сравнения. Предположим, что: SP={ (SP_k, SP_kt) | k = 1, ..., n } обозначает извлеченные PIPs из последовательности P, SP_k и SP_kt соответственно обозначают координату амплитуды и координату времени PIPs последовательности P; и Q={(Q_k,Q_kt) | k = 1,..., n} имеет тот же смысл. Взять и временное искажение, и искажение амплитуды при рассмотрении меры расстояния, определенной в [1], как указано ниже:

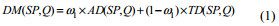
где, AD(SP, Q) расстояние амплитуды и может быть сформулировано, как указано ниже:

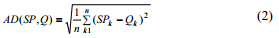
в то время как TD(SP, Q) обозначает временное расстояние и может быть вычислено как указано ниже:

w1 обозначает весовой коэффициент для амплитуды расстояния и временного расстояния, который может быть рассмотрен в качестве параметра и может быть определен пользователем.

2.3. Приобретенные и исключенные проблемы PIPs

В ссылке [1], необходимо число PIPs для каждого сегмента такое, чтобы соответствовать длине шаблона. Следовательно, проблемы могут быть у добавленных PIPs или у потерянных, когда количество очевидно колеблющихся пунктов в сегменте более или менее, чем длина соответствующего шаблона (см. Рисунок 1).

Рисунок 1 – PIPs добавил и потерял проблемы; (a) – в третьем PIP сегмент является не колеблющимся и является избыточным; (b) – пропустит два очка соответственно между 3м и 4м , 6м и 7м.

Мера расстояния по формуле (1) основана на DPPD. Это нестабильное состояние, когда есть PIPs, которые приобрели или потеряли проблемы. На Рисунке 1 изображено: (a) – частично добавленный PIP между 2й, без обозначения даты, и 4й точкой (точка-точка), нанесенный на карту после 3го PIP, и деформирующий точку, которая приводит к деформации вычисления расстояния передачи точек. Та же самое происходит, когда есть потерянные PIPs проблемы. Поэтому, расстояние по формуле (1) для двух подобных последовательностей все еще очень большое, когда PIPs приобрели или потеряли проблемы. В этом случае мера по DPPD может не отражать фактическое расстояние двух последовательностей хорошо.

Предлагаемые меры расстояния

Во втором разделе, были подробно проанализированы недостатки DPPD-подхода. На самом деле, существуют и другие, более качественные подходы к измерению подобия двух последовательностей. Ниже представлены три из них.

3.1. Ограничение области расстояния (EAD)

Область, заключенная между временной последовательностью и шаблоном (образцом) будет естественным определением для измерения расстояния в интуиции. Обратите внимание на тень на Рисунке 2. Когда последовательность подобна шаблону образца, ограниченная область будет меньшей. Если последовательность подобна заданному шаблону, включенная область будет равна 0 и наоборот.

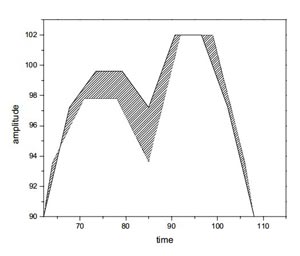
Рисунок 2 – Ограниченная область

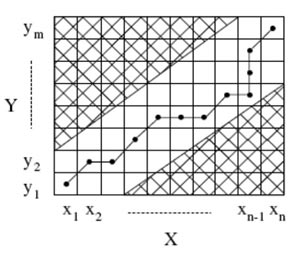
Рисунок 3 – Деформированный (искривленный) путь

Таким образом, огражденная область удовлетворяет монотонному (линейному) свойству, которое рассматривают как важный фактор в определение функции пригодности (fitness-функции). Предположим f(x) и g(x) соответственно обозначив кривую функции сегмента времени и шаблона, тогда включенная область D_ea (SP, Q) может может быть вычислена как указано ниже:

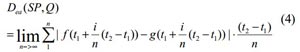
В качестве приближенного вычисления площадей, вычисляется только сумма |f(x)-g(x)| на промежутке [t1, t2] особенно, когда n является длиной интервала [t1, t2]. Кроме того, огороженная область коротких последовательностей всегда меньше, чем длинных. Следовательно, нужно взять среднее число огороженной области, как меру расстояния, чтобы сделать его объективным на малых последовательностях. Новая формула представлена ниже:

Литература

1. L. Chung, T. C. Fu, and R. Luk, “An evolutionary approach to pattern-based time series segmentation,” IEEE Trans. Evol. Comput., vol. 8, vol. 5, Oct. 2004, pp. 471-489.
2. Das, K. I. Lin, and H. Mmmila, “Rule discovery from time series,” in Proc. ACM SIGKDD Int. Conf. Knowledge Discovery Data Mining, 1998, pp. 16-22.
3. Y. Kai, W. Jia, P. Zhou, and X. Meng, “A new approach to transforming time series into symbolic sequences,” in Proc. 1st joint BMES/EMBS Conf., Oct. 1999, vol. 2, p. 974.
4. J. Oliver, R. A. Baxter, and C. S. Wallace, “Minimum message length segmentation,” in Proc. Pacific-Asia Conf. Knowledge Discovery Data Mining, 1998, pp. 222-233.
5. J. Oliver and C. S. Forbes, “Bayesian approaches to segmenting a simple time series,” Dept. Comput. Sci., Monash Univ., Victoria, Astralia, Tech. Rep. 97/336, 1997.
6. Han, W. Gong, and Y. Tin, “Mining segment-wise periodic patterns in time-related databases,” in Proc. Int. Conf. Knowledge Discovery Data Mining, 1998, pp. 214-218.
7. Han, G. Dong, and Y. Yin, “Efficient mining of partial periodic patterns in time series database,” in Proc. 15th Int. Conf. on Data Engineering: IEEE Computer Society Press, 1999, pp. 106-115.
8. C. Fu, F. L. Chung, V. Ng, and R. Luk, “Evolutionary segmentation of financial time series into subsequences,” in Proc. Congr. Evolutionary Computation, Seoul, Korea, 2001, pp. 426-430.
9. Xiao, X. F. Feng, and Y. F. Hu, “A new segmented time warping distance for data mining in time series database,” in Proc. 3th Int. Conf. Machine Learning and Cybemetics. Shanghai, Aug. 2004, pp. 1277-1281.
10. Wong and M. H. Wong, “Efficient subsequence matching for sequences databases under time Warping,” in Proc. 7th Int. Conf. Database Engineering and Applications Symposium, 2003, p.139.
11. Rabiner and B.-H. Juang, “Fundamentals of Speech Recognition,” Prentice Hall, 1993.
12. S. Lei and V. Govindaraju, “Regression time warping for similarity measure of sequence,” in Proc. 4th Int. Conf. on Computer and Information Technology, 2004, pp. 826-830.
13. D.Wang and G. Rong, “Pattern distance of time series”, Journal of Zhejiang University (Engineering Science), vol. 38, no. 7, Jul. 2004, pp. 795-798.
14. YOON J, L. EE. J, and KIM. S, “Trend similarity and prediction in time series databases,” in Proceedings of SPIE on Data Mining and Knowledge Discovery: Theory, Tools, and Technology II [C], Washington: SPIE, 2000, pp. 201-212.
15. Wang, G. Rong, and H. L. Li, “Variable setp algorithm for sub-trend sequence searching”, Journal of Zhejiang University (Engineering Science), vol. 38, no. 12, Dec. 2004, pp. 1566-1569.
16. Z. Yu, H. Peng, and Q. L. Zheng, “Pattern distance of time series based on segmentation by important points,” in Proc. 4th Int. Conf. on Machine Learning and Cybemetics, Aug. 2005, pp. 1563-1567.

Назад в библиотеку