Аннотация
Сиротюк Е.Я., Васяева Т.А. Отбор оптимальной регрессионной модели для прогнозирования перинатального риска с помощью метода группового учета аргументов. Разработан метод выбора оптимальной регрессионной модели для прогнозирования перинатального риска. Рассматривается сопутствующая задача отбора факторов риска, влияющих на перинатальный риск у беременных.
Введение
Ежедневно в мире от осложнений, связанных с беременностью и родами, умирает 1500 женщин. По оценкам экспертов большинство этих случаев можно было предотвратить. В настоящее время в медицине особое значение приобретает направление, связанное со снижением перинатальной смертности.
Наиболее действенный путь в снижении перинатальной смертности лежит в разработке программ прогнозированиях перинатального риска [1]. Сложность их разработки заключается в необходимости научного анализа большого количества клинических и лабораторных показателей, которые находятся в сложной зависимости друг от друга и не всегда поддаются количественной оценке [2].
Постановка проблемы
Достаточно часто для решения задачи прогнозирования используются регрессионные модели. Для построения регрессионной модели необходимо выполнить отбор необходимых факторов и затем рассчитать коэффициенты уравнения. При выборе того или иного набора параметров можно получать различные регрессионные модели, причем многие из них будут показывать хорошие результаты. Всегда при построении математической функции классификации или регрессии основная задача сводится к выбору наилучшей модели из всего множества вариантов. Однако может существовать множество функций, одинаково классифицирующих одну и ту же обучающую выборку (рис. 1).
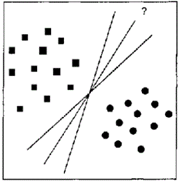
Рисунок 1 – Варианты линейного разделения обучающей выборки
Теория множественности моделей [3] утверждает, что по экспериментальным данным принципиально нельзя найти единственную модель. Например, в качестве полинома регрессии можно взять полином любого вида и любой степени, и для каждого из них регрессионный анализ укажет значения коэффициентов. Решение вопроса о выборе единственного уравнения регрессии оптимальной сложности дает принцип внешнего дополнения. Только внешний критерий приводит к единственной модели оптимальной сложности.
Разработка алгоритма
В большинстве случаев, в медицинских задачах, результат прогнозирования зависит от большого количества неодинаковых по значимости факторов, которые к тому же могут быть взаимосвязаны. Этот факт значительно усложняет этап отбора данных, исключая возможность использовать большую часть известных методов. Отбор данных для анализа выполняется врачом по следующему принципу: сначала осуществляется выделение факторов риска, относящихся к определенной патологии, затем группы факторов риска определяются временем их воздействия, видом (биологические, средовые и т.д.) и количеством воздействующих факторов. При анализе данных, предоставленных различными врачами для прогнозирования тех или иных заболеваний в области гинекологии можно сделать вывод, что перечень собранных факторов является относительно стабильным, причем одинаковым для анализа большинства гинекологических проблем и очень большим. В него входят медицинские и социально-демографические факторы.
Однако выделение факторов риска является не единственной задачей, также необходимо оценить роль каждого из них. Из этого следует, что значимость каждого фактора на риск развития различных акушерских осложнений будет различна [4]. Тем не менее, отбор факторов риска является одним из самых важных этапов построения прогнозирующей модели и в значительной степени определяет ее качество.
Полный перебор регрессионных моделей, даже в пределах заданной опорной функции, при достаточно большом наборе входных параметров на практике реализовать не представляется возможным. Для достаточно сложных задач моделирования (например, большой набор обучающих данных) применяются многорядные алгоритмы метода группового учета аргументов (МГУА) [3]. Многорядный алгоритм МГУА исключает из перебора некоторые модели благодаря наличию порогов.
Предварительно в многорядном (пороговом) алгоритме МГУА на вход подается некоторый вектор входных переменных x = x1, x2,..., xn. На первом ряду селекции образуются «частные описания» (1) – (3), объединяющие входные переменные по две:
| |
(1) |
| |
(2) |
...
| |
(3) |
Из них выбирается некоторое число моделей наиболее удовлетворяющих внешнему критерию селекции. В нашем случае в качестве такого критерия будет среднеквадратичная ошибка (4) на проверочных данных.
 |
(4) |
где М – количество обучающих примеров, F – полученный результат, Y – действительный результат.
На втором ряду образуются «частные описания» второго ряда:
| |
(5) |
...
| |
(6) |
...
| (7) |
Из них также выбирается некоторое количество наилучших для использования в следующем, третьем ряду и т.д. Для каждого ряда находится наилучшая (по критерию селекции) модель (рис. 2). Ряды селекции наращиваются, пока оценка критерия уменьшается («правило останова»). На последнем ряду лучшая модель будет оптимальной. Коэффициенты в регрессионных моделях рассчитываются методом наименьших квадратов (МНК).

Рисунок 2 – Многорядный МГУА
Выводы
Рассмотрена актуальная задача отбора оптимальной регрессионной модели, для прогнозирования перинатального риска, включая задачу отбора факторов риска. В дальнейшем планируется реализовать рассмотренный математический аппарат и протестировать на реальных медицинских данных, предоставленных сотрудниками центра материнства и детства. Также планируется разработка и внедрение системы прогнозирования перинатального риска.
Список использованной литературы
- Радзинский В.Е. Акушерский риск. Максимум информации минимум опасности для матери и младенца. / В.Е. Радзинский, С.А. Князев, И.Н. Костин. – Изд.: Эксмо. – 2009 г. – С. 285
- Т.А. Васяева Применение метода группового учета аргументов для отбора оптимальной регрессионной модели прогнозирования потери крови при родах// Т.А. Васяева/ Вестник Херсонского национального технического университета. – 2012. – № 1(44). – С. 374.
- Ивахненко А.Г. Самоорганизация прогнозирующих моделей / Ивахненко А.Г., Мюллер И.А. – К.: Техника, 1985. – 223 с.
- Т.А. Васяева Анализ методов отбора факторов риска развития патологий в акушерстве и гинекологии / Т.А. Васяева, Д.Е. Иванов, И.В. Соков, А.С. Сокова // Збірка матеріалів ІІ Всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених.ІУС КМ-2011 11–13 квітня 2011р., Донецьк: ДонНТУ, 2011. – № 1. – С. 209–212.