Принципы построения параллельных вычислительных систем

Авторы: Гергель В.П., Стронгин Р.Г.
Источник: Основы параллельных вычислений для многопроцессорных вычислительных систем. Учебное пособие. Издание 2-е, дополненное. Издательство Нижегородского госуниверситета, Нижний Новгород. – 2003. [Электронный ресурс]. – Режим доступа: http://www.hpcc.unn.ru/files/HTML_Version/part1.html

1. Пути достижения параллелизма

В общем плане под параллельными вычислениями понимаются процессы обработки данных, в которых одновременно могут выполняться нескольких машинных операций. Достижение параллелизма возможно только при выполнимости следующих требований к архитектурным принципам построения вычислительной системы:

• независимость функционирования отдельных устройств ЭВМ – данное требование относится в равной степени ко всем основным компонентам вычислительной системы – к устройствам ввода-вывода, к обрабатывающим процессорам и к устройствам памяти;
• избыточность элементов вычислительной системы – организация избыточности может осуществляться в следующих основных формах:
• использование специализированных устройств таких, например, как отдельных процессоров для целочисленной и вещественной арифметики, устройств многоуровневой памяти (регистры, кэш);
• дублирование устройств ЭВМ путем использования, например, нескольких однотипных обрабатывающих процессоров или нескольких устройств оперативной памяти.

Дополнительной формой обеспечения параллелизма может служить конвейерная реализация обрабатывающих устройств, при которой выполнение операций в устройствах представляется в виде исполнения последовательности составляющих операцию подкоманд; как результат, при вычислениях на таких устройствах могут находиться на разных стадиях обработки одновременно несколько различных элементов данных.

Возможные пути достижения параллелизма детально рассматриваются в [22, 29]; в этой же работе рассматривается история развития параллельных вычислений и приводятся примеры конкретных параллельных ЭВМ (см. также [9, 29, 31]).

При рассмотрении проблемы организации параллельных вычислений следует различать следующие возможные режимы выполнения независимых частей программы:

• многозадачный режим (режим разделения времени), при котором для выполнения процессов используется единственный процессор; данный режим является псевдопараллельным, когда активным (исполняемым) может быть один единственный процесс, а все остальные процессы находятся в состоянии ожидания своей очереди на использование процессора; использование режима разделения времени может повысить эффективность организации вычислений (например, если один из процессов не может выполняться из-за ожидании вводимых данных, процессор может быть задействован для готового к исполнению процесса – см. [6, 13]), кроме того, в данном режиме проявляются многие эффекты параллельных вычислений (необходимость взаимоисключения и синхронизации процессов и др.) и, как результат, этот режим может быть использован при начальной подготовке параллельных программ;
• параллельное выполнение, когда в один и тот же момент времени может выполняться несколько команд обработки данных; данный режим вычислений может быть обеспечен не только при наличии нескольких процессоров, но реализуем и при помощи конвейерных и векторных обрабатывающих устройств;
• распределенные вычисления; данный термин обычно используют для указания параллельной обработки данных, при которой используется несколько обрабатывающих устройств, достаточно удаленных друг от друга и в которых передача данных по линиям связи приводит к существенным временным задержкам; как результат, эффективная обработка данных при таком способе организации вычислений возможна только для параллельных алгоритмов с низкой интенсивностью потоков межпроцессорных передач данных; перечисленные условия является характерными, например, при организации вычислений в многомашинных вычислительных комплексах, образуемых объединением нескольких отдельных ЭВМ с помощью каналов связи локальных или глобальных информационных сетей.

В рамках данного пособия основное внимание будет уделяться второму типу организации параллелизма, реализуемому на многопроцессорных вычислительных системах.

2. Классификация вычислительных систем

Одним из наиболее распространенных способов классификации ЭВМ является систематика Флинна (Flynn), в рамках которой основное внимание при анализе архитектуры вычислительных систем уделяется способам взаимодействия последовательностей (потоков) выполняемых команд и обрабатываемых данных. В результате такого подхода различают следующие основные типы систем [9, 22, 29, 31]:

• SISD (Single Instruction, Single Data) – системы, в которых существует одиночный поток команд и одиночный поток данных; к данному типу систем можно отнести обычные последовательные ЭВМ;
• SIMD (Single Instruction, Multiple Data) – системы c одиночным потоком команд и множественным потоком данных; подобный класс систем составляют МВС, в которых в каждый момент времени может выполняться одна и та же команда для обработки нескольких информационных элементов;
• MISD (Multiple Instruction, Single Data) – системы, в которых существует множественный поток команд и одиночный поток данных; примеров конкретных ЭВМ, соответствующих данному типу вычислительных систем, не существует; введение подобного класса предпринимается для полноты системы классификации;
• MIMD (Multiple Instruction, Multiple Data) – системы c множественным потоком команд и множественным потоком данных; к подобному классу систем относится большинство параллельных многопроцессорных вычислительных систем.

Следует отметить, что хотя систематика Флинна широко используется при конкретизации типов компьютерных систем, такая классификация приводит к тому, что практически все виды параллельных систем (несмотря на их существенную разнородность) относятся к одной группе MIMD. Как результат, многими исследователями предпринимались неоднократные попытки детализации систематики Флинна. Так, например, для класса MIMD предложена практически общепризнанная структурная схема [29, 31], в которой дальнейшее разделение типов многопроцессорных систем основывается на используемых способах организации оперативной памяти в этих системах (см. рис. 1.1). Данный поход позволяет различать два важных типа многопроцессорных систем – multiprocessors (мультипроцессоры или системы с общей разделяемой памятью) и multicomputers (мультикомпьютеры или системы с распределенной памятью).

Далее для мультипроцессоров учитывается способ построения общей памяти. Возможный подход – использование единой (централизованной) общей памяти. Такой подход обеспечивает однородный доступ к памяти (uniform memory access or UMA) и служит основой для построения векторных суперкомпьютеров (parallel vector processor, PVP) и симметричных мультипроцессоров (symmetric multiprocessor or SMP). Среди примеров первой группы суперкомпьютер Cray T90, ко второй группе относятся IBM eServer p690, Sun Fire E15K, HP Superdome, SGI Origin 300 и др.

Общий доступ к данным может быть обеспечен и при физически распределенной памяти (при этом, естественно, длительность доступа уже не будет одинаковой для всех элементов памяти). Такой подход именуется как неоднородный доступ к памяти (non-uniform memory access or NUMA). Среди систем с таким типом памяти выделяют:

• Системы, в которых для представления данных используется только локальная кэш память имеющихся процессоров (cache-only memory architecture or COMA); примерами таких систем являются, например, KSR-1 и DDM;
• Системы, в которых обеспечивается однозначность (когерентность) локальных кэш памяти разных процессоров (cache-coherent NUMA or CC-NUMA); среди систем данного типа SGI Origin2000, Sun HPC 10000, IBM/Sequent NUMA-Q 2000;
• Системы, в которых обеспечивается общий доступ к локальной памяти разных процессоров без поддержки на аппаратном уровне когерентности кэша (non-cache coherent NUMA or NCC-NUMA); к данному типу относится, например, система Cray T3E.

Мультикомпьютеры (системы с распределенной памятью) уже не обеспечивают общий доступ ко всей имеющейся в системах памяти (no-remote memory access or NORMA). Данный подход используется при построении двух важных типов многопроцессорных вычислительных систем – массивно-параллельных систем (massively parallel processor or MPP) и кластеров (clusters). Среди представителей первого типа систем – IBM RS/6000 SP2, Intel PARAGON/ASCI Red, транспьютерные системы Parsytec и др.; примерами кластеров являются, например, системы AC3 Velocity и NCSA/NT Supercluster.

Следует отметить чрезвычайно быстрое развитие кластерного типа многопроцессорных вычислительных систем – современное состояние данного подхода отражено, например, в обзоре, подготовленном под редакцией Barker (2000). Под кластером обычно понимается (см., например, Xu and Hwang (1998), Pfister (1998)) множество отдельных компьютеров, объединенных в сеть, для которых при помощи специальных аппаратно-программных средств обеспечивается возможность унифицированного управления (single system image), надежного функционирования (availability) и эффективного использования (performance). Кластеры могут быть образованы на базе уже существующих у потребителей отдельных компьютеров либо же сконструированы из типовых компьютерных элементов, что обычно не требует значительных финансовых затрат. Применение кластеров может также в некоторой степени снизить проблемы, связанные с разработкой параллельных алгоритмов и программ, поскольку повышение вычислительной мощности отдельных процессоров позволяет строить кластеры из сравнительно небольшого количества (несколько десятков) отдельных компьютеров (lowly parallel processing). Это приводит к тому, что для параллельного выполнения в алгоритмах решения вычислительных задач достаточно выделять только крупные независимые части расчетов (coarse granularity), что, в свою очередь, снижает сложность построения параллельных методов вычислений и уменьшает потоки передаваемых данных между компьютерами кластера. Вместе с этим следует отметить, что организации взаимодействия вычислительных узлов кластера при помощи передачи сообщений обычно приводит к значительным временным задержкам, что накладывает дополнительные ограничения на тип разрабатываемых параллельных алгоритмов и программ.

В завершении обсуждаемой темы можно отметить, что существуют и другие способы классификации вычислительных систем (достаточно полный обзор подходов представлен в [22], см. также материалы сайта http://www.parallel.ru/computers/taxonomy/); при рассмотрении данной темы параллельных вычислений рекомендуется обратить внимание на способ структурной нотации для описания архитектуры ЭВМ, позволяющий с высокой степенью точности описать многие характерные особенности компьютерных систем.

3. Характеристика типовых схем коммуникации в многопроцессорных вычислительных системах

При организации параллельных вычислений в МВС для организации взаимодействия, синхронизации и взаимоисключения параллельно выполняемых процессов используется передача данных между процессорами вычислительной среды. Временные задержки при передаче данных по линиям связи могут оказаться существенными (по сравнению с быстродействием процессоров) и, как результат, коммуникационная трудоемкость алгоритма оказывает существенное влияние на выбор параллельных способов решения задач.

Структура линий коммутации между процессорами вычислительной системы (топология сети передачи данных) определяется, как правило, с учетом возможностей эффективной технической реализации; немаловажную роль при выборе структуры сети играет и анализ интенсивности информационных потоков при параллельном решении наиболее распространенных вычислительных задач. К числу типовых топологий обычно относят следующие схемы коммуникации процессоров (см. рис. 1.1):

• полный граф (completely-connected graph or clique) - система, в которой между любой парой процессоров существует прямая линия связи; как результат, данная топология обеспечивает минимальные затраты при передаче данных, однако является сложно реализуемой при большом количестве процессоров;
• линейка (linear array or farm) – система, в которой каждый процессор имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами; такая схема является, с одной стороны, просто реализуемой, а с другой стороны, соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений);
• кольцо (ring) – данная топология получается из линейки процессоров соединением первого и последнего процессоров линейки;
• звезда (star) – система, в которой все процессоры имеют линии связи с некоторым управляющим процессором; данная топология является эффективной, например, при организации централизованных схем параллельных вычислений;
• решетка (mesh) – система, в которой граф линий связи образует прямоугольную сетку (обычно двух- или трех- мерную); подобная топология может быть достаточно просто реализована и, кроме того, может быть эффективно используема при параллельном выполнении многих численных алгоритмов (например, при реализации методов анализа математических моделей, описываемых дифференциальными уравнениями в частных производных);
• гиперкуб (hypercube) – данная топология представляет частный случай структуры решетки, когда по каждой размерности сетки имеется только два процессора (т.е. гиперкуб содержит 2N процессоров при размерности N); данный вариант организации сети передачи данных достаточно широко распространен в практике и характеризуется следующим рядом отличительных признаков:
• два процессора имеют соединение, если двоичное представление их номеров имеет только одну различающуюся позицию;
• в Nмерном гиперкубе каждый процессор связан ровно с N соседями;
• N-мерный гиперкуб может быть разделен на два (N–1)-мерных гиперкуба (всего возможно N различных таких разбиений);
• кратчайший путь между двумя любыми процессорами имеет длину, совпадающую с количеством различающихся битовых значений в номерах процессоров (данная величина известна как расстояние Хэмминга).

Дополнительная информация по топологиям МВС может быть получена, например, в [9, 22 – 23, 29, 31]; при рассмотрении вопроса следует учесть, что схема линий передачи данных может реализовываться на аппаратном уровне, а может быть обеспечена на основе имеющейся физической топологии при помощи соответствующего программного обеспечения. Введение виртуальных (программно-реализуемых) топологий способствует мобильности разрабатываемых параллельных программ и снижает затраты на программирование.

4. Высокопроизводительный вычислительный кластер ННГУ

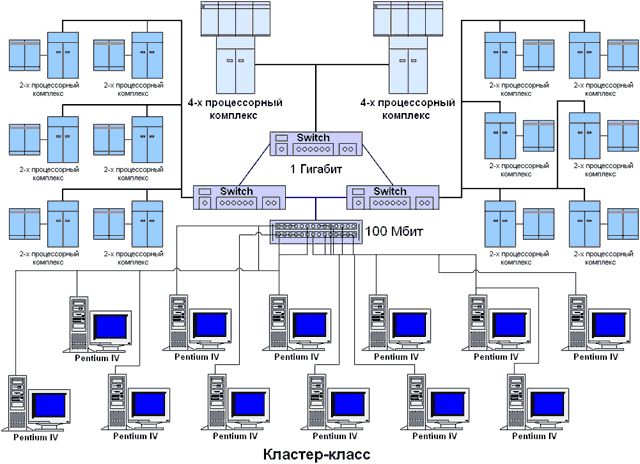
Для проведения вычислительных экспериментов использовался вычислительный кластер Нижегородского университета, оборудование для которого было передано в рамках Академической программы Интел в 2001 г. В состав кластера входит (см. рис. 1.3):

• 2 вычислительных сервера, каждый из которых имеет 4 процессора Intel Pentium III 700 Мгц, 512 MB RAM, 10 GB HDD, 1 Гбит Ethernet card;
• 12 вычислительных серверов, каждый из которых имеет 2 процессора Intel Pentium III 1000 Мгц, 256 MB RAM, 10 GB HDD, 1 Гбит Ethernet card;
• 12 рабочих станций на базе процессора Intel Pentium 4 1300 Мгц, 256 MB RAM, 10 GB HDD, CD-ROM, монитор 15", 10/100 Fast Ethernet card.

Следует отметить, что в результате передачи подобного оборудования Нижегородский госуниверситет оказался первым вузом в Восточной Европе, оснащенным ПК на базе новейшего процессора INTEL® PENTIUM® 4. Подобное достижение является дополнительным подтверждением складывающегося плодотворного сотрудничества ННГУ и корпорации Интел.

Важной отличительной особенностью кластера является его неоднородность (гетерогенность). В состав кластера входят рабочие места, оснащенные новейшими процессорами Intel Pentium 4 и соединенные относительно медленной сетью (100 Мбит), а также вычислительные 2- и 4- процессорные сервера, обмен данными между которыми выполняется при помощи быстрых каналов передачи данных (1000 Мбит). В результате кластер может использоваться не только для решения сложных вычислительно-трудоемких задач, но также и для проведения различных экспериментов по исследованию многопроцессорных кластерных систем и параллельных методов решения научно-технических задач.

В качестве системной платформы для построения кластера выбраны современные операционные системы семейства Microsoft Windows (для проведения отдельных экспериментов имеется возможность использования ОС Unix). Выбор такого решения определяется рядом причин, в числе которых основными являются следующие моменты:

• операционные системы семейства Microsoft Windows (так же как и ОС Unix) широко используются для построения кластеров; причем, если раньше применение ОС Unix для этих целей было преобладающим системным решением, в настоящее время тенденцией является увеличение числа создаваемых кластеров вод управлением ОС Microsoft Windows;
• разработка прикладного программного обеспечения выполняется преимущественно с использованием ОС Microsoft Windows;
• корпорация Microsoft проявила заинтересованность в создании подобного кластера и передала в ННГУ для поддержки работ все необходимое программное обеспечение (ОС MS Windows 2000 Professional, ОС MS Windows 2000 Advanced Server и др.).

В результате принятых решений программное обеспечение кластера является следующим:

• вычислительные сервера работают под управлением ОС Microsoft Windows 2000 Advanced Server; на рабочих местах разработчиков установлена ОС Microsoft Windows 2000 Professional;
• в качестве сред разработки используются Microsoft Visual Studio 6.0; для выполнения исследовательских экспериментов возможно использование компилятора Intel C++ Compiler 5.0, встраиваемого в среду Microsoft Visual Studio;
• на рабочих местах разработчиков установлены библиотеки:
• Plapack 3.0 (см. www.cs.utexas.edu/users/plapack);
• MKL (см. developer.intel.com/software/products/mkl/index.htm);
• в качестве средств передачи данных между процессорами установлены две реализации стандарта MPI:
• Argonne MPICH;
• MP-MPICH.
• в опытной эксплуатации находится система разработки параллельных программ DVM (см. www.keldysh.ru/dvm/).

Литература

1. Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. – Н.Новгород, ННГУ, 2001.
2. Богачев К.Ю. Основы параллельного программирования. – М.:БИНОМ. Лаборатория знаний, 2003.
3. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002.
4. Немнюгин С., Стесик О. Параллельное программирование для многопроцессорных вычислительных систем – СПб.: БХВ-Петербург, 2002.
5. Березин И.С., Жидков И.П. Методы вычислений. – М.: Наука, 1966.
6. Дейтел Г. Введение в операционные системы. Т.1.- М.: Мир, 1987.
7. Кнут Д. Искусство программирования для ЭВМ. Т. 3. Сортировка и поиск. – М.: Мир, 1981.
8. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: МЦНТО, 1999.
9. Корнеев В.В.. Параллельные вычислительные системы. – М.: Нолидж, 1999.
10. Корнеев В.В. Параллельное программирование в MPI. Москва-Ижевск: Институт компьютерных исследований, 2003.
11. П.Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.:Наука, 1977.
12. Хамахер К., Вранешич З., Заки С. Организация ЭВМ. – СПб: Питер, 2003.
13. Шоу А. Логическое проектирование операционных систем. – М.: Мир, 1981.
14. Andrews G.R. Foundations of Multithreading, Parallel and Distributed Programming. Addison-Wesley, 2000 (русский перевод Эндрюс Г.Р. Основы многопоточного, параллельного и распределенного программирования. – М.: Издательский дом "Вильяме", 2003)
15. Barker, M. (Ed.) (2000). Cluster Computing Whitepaper http://www.dcs.port.ac.uk/~mab/tfcc/WhitePaper/.
16. Braeunnl Т. Parallel Programming. An Introduction.- Prentice Hall, 1996.
17. Chandra, R., Menon, R., Dagum, L., Kohr, D., Maydan, D., McDonald, J. Parallel Programming in OpenMP. – Morgan Kaufinann Publishers, 2000.
18. Dimitri P. Bertsekas, John N. Tsitsiklis. Parallel and Distributed Computation. Numerical Methods. – Prentice Hall, Englewood Cliffs, New Jersey, 1989.
19. Fox G.C. et al. Solving Problems on Concurrent Processors. – Prentice Hall, Englewood Cliffs, NJ, 1988.
20. Geist G.A., Beguelin A., Dongarra J., Jiang W., Manchek В., Sunderam V. PVM: Parallel Virtual Machine – A User's Guide and Tutorial for Network Parallel Computing. MIT Press, 1994.
21. Group W, Lusk E, Skjellum A. Using MPI. Portable Parallel Programming with the Message-Passing Interface. – MIT Press, 1994. (http://www.mcs.anl.gov/mpi/index.html)
22. Hockney R. W., Jesshope C.R. Parallel Computers 2. Architecture, Programming and Algorithms. – Adam Hilger, Bristol and Philadelphia, 1988. (русский перевод 1 издания: Р.Xокни, К.Джессхоуп. Параллельные ЭВМ. Архитектура, программирование и алгоритмы. – М.: Радио и связь, 1986)
23. Kumar V., Grama A., Gupta A., Karypis G. Introduction to Parallel Computing. – The Benjamin/Cummings Publishing Company, Inc., 1994.
24. Miller R., Boxer L. A Unified Approach to Sequential and Parallel Algorithms. Prentice Hall, Upper Saddle River, NJ. 2000.
25. Pacheco, S. P. Parallel programming with MPI. Morgan Kaufmann Publishers, San Francisco. 1997.
26. Parallel and Distributed Computing Handbook. / Ed. A.Y. Zomaya. - McGraw-Hill, 1996.
27. Pfister, G. P. In Search of Clusters. Prentice Hall PTR, Upper Saddle River, NJ 1995. (2nd edn., 1998).
28. Quinn M. J. Designing Efficient Algorithms for Parallel Computers. – McGraw-Hill, 1987.
29. Rajkumar Buyya. High Performance Cluster Computing. Volume l: Architectures and Systems. Volume 2: Programming and Applications. Prentice Hall PTR, Prentice-Hall Inc., 1999.
30. Roosta, S.H. Parallel Processing and Parallel Algorithms: Theory and Computation. Springer-Verlag, NY. 2000.
31. Xu, Z., Hwang, K. Scalable Parallel Computing Technology, Architecture, Programming. McGraw-Hill, Boston. 1998.
32. Wilkinson В., Allen M. Parallel programming. – Prentice Hall, 1999.

Информационные ресурсы сети Интернет

33. Информационно-аналитические материалы по параллельным вычислениям (http://www.parallel.ru)
34. Информационные материалы Центра компьютерного моделирования Нижегородского университета (http://www.software.unn.ac.ru/ccam)
35. Foster I. Designing and Building Parallel Programs. – Addison Wesley, 1994. (http://www.mcs.anl.gov/dbpp)