Проблемно-орієнтоване паралельне моделююче середовище для динамічних мережних об'єктів
Авторы: Святний B.A., Молдованова O.B., Перерва А.О.
Источник: Наукові праці Донецького національного технічного університету. Серiя «Проблеми моделювання та автоматизації проектування» (МАП-2001). Випуск: 29 – Донецьк: ДонНТУ. – 2001.
Abstract
Svjatnyj V.A., Motdovanova O.V., Pererva A.O. Problem oriented parallel simulation environment for dynamic network objects: The article describes main features of dynamic network objects and offers a problem oriented parallel simulation environment as a mean of object modelling and simulation. The represented simulation environment consists of two parts: hardware and software parts. The hardware part contains computing systems of SIMD- and MIMD-architectures and clusters of PCs, which work by MTMD-principle. The software part consists of a topological analyser, an equation generator and two equation solvers for an object with concentrated and distributed parameters correspondingly). The software part contains tools to visualize the simulation results. Structures and algorithms of all software elements are described in the article. The results of experimental researches are also given in the article.
1. Bcтyп
Динамічні об'єкти, що мають структуру мережі, належать до поширеного класу складних технічних систем енергетики, гірничої справи, газо- і водопостачання, хімічних технологій. Формальний опис об'єктів складається із двох суттєвих частин: опису топології та рівнянь фізичних процесів, що мають місце в гілках та вузлах мереж. 3 огляду на велику кількість гілок та вузлів, нелінійність рівнянь, розподіленість параметрів процесів мережні об'єкти майже не піддаються аналітичному дослідженню, тому основним методом підтримки технологічного проектування і вирішення задач автоматизації є математичне моделювання. Розглянемо питання системної організації засобів моделювання та методику побудови моделей цього класу об'єктів.
2. Формальний опис мережних об'єктів
Мережні об'єкти характеризуються топологією зв'язків між гілками та вузлами, розташуванням активних елементів (насоси, компресори, генератори, вентилятори та ін.) в мережі та фізичними процесами динаміки потоків (рідин, газів, повітря, електричного струму та ін.) в гілках та вузлах.
Топологія мережного об'єкта представляється орієнтованим сильно зв'язним графом G(m,n) з числами гілок m та вузлів n. Мережі реальної складності мають такі особливості: відносно велика кількість гілок та вузлів (m > 100, n > 50); різноманітність технологічного призначення елементів топології; фізичні параметри гілок та вузлів можуть бути змінними величинами, як в функції часу, так і інших параметрів; теоретично в кожній гілці графа може знаходитися активний елемент, що впливає на динаміку потоків; в період експлуатації топологія мережних об'єктів зазнає змін (з'являються нові гілки та вузли, можуть зникати відпрацьовані елементи топологій). На рис. 1 показано приклад шахтної вентиляційної мережі з m=117, n=61.
Топологію графа G(m,n) пропонується формально описувати таблицею, що має m рядків та s+5 колонок з наступними іменами-ідентифікаторами:
AKJ EKJ OI PAR(PI1, PI2,...,PIs) AEI VECOMI (1)
де AKJ, EKJ – номери початкових та кінцевих вузлів гілки QI (фізичний потік Q та номер гілки I), J = (l, 2,...,n), I = (l, 2,...,m); PAR(PI1, PI2,...,PIs) – множина s параметрів PI кожної гілки; AEI – активний елемент в І-й гілці; VECOMI – вербальний коментар, що пояснює технологічне призначення І- ї гілки.
Другою складовою частиною формального опису мережних об'єктів є диференціальні рівняння динамічних процесів в гілках та вузлах. Отримання рівнянь є основною задачею теорії мережних об'єктів в усіх без винятку предметних областях. B мережах розподілу фізичних потоків (гідравліка, пневматика, вентиляція, газодинаміка, електротехніка, ряд технологій) рівняння виводяться за такою методикою:
- в гілці виділяється безкінечно малий об'єм dv=dxdydz;
- аналізуються сили, що діють на об'єм на безкінечно малому інтервалі часу dt, записуються рівняння руху потоку та його нерозривності; для деяких об'єктів в цьому ж об'єкті можуть аналізуватися декілька процесів (дифузія домішків, фазове перетворення та ін.);
- переходом від безкінечно малих параметрів отримують систему диференціальних рівнянь у часткових похідних для І-ї гілки;
- на основі аналізу умов на кінцях формулюють крайову динамічну задачу для І-ї гілки графа;
- математичний опис графа мережі буде складатись з m гілкових систем рівнянь та n крайових (вузлових) умов.
Так, для І- ї гілки шахтної вентиляційної мережі (ШВМ , рис. 1) маємо систему рівнянь [1]:
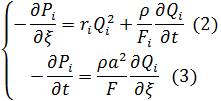
в якій Pi, Qi – тиск та потік повітря вздовж координати ξ, що відраховується від початкового AKJ до кінцевого EKJ вузлів; r, F – питомий аеродинамічний опір та площа поперечного розтину (гірнича виробка); p, а – густина повітря та швидкість розповсюдження звуку в повітрі.
Крайові умови для рівнянь (2), (3) – це функції тиску в початковому Рbeg та кінцевому Рend вузлах гілки QI. За видами крайових умов гілки мережі поділяються на три типи:
- гілки, інцидентні внутрішнім вузлам мережі, в яких тиск підраховується в процесі вирішення мережної системи рівнянь відповідно до вузлових динамічних умов
- гілки, що інцидентні вузлу підключення вентилятора; в цьому вузлі тиск задається як характеристика вентилятора
- гілки, що інцидентні вузлу виходу в атмосферу; тут має прийматись постійний тиск атмосфери
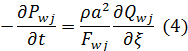
Pwj=PAEI(QI) (5)
Pwj=PATM=const (6)
Таким чином, мережний об'єкт з розподіленими параметрами з топологією (1) описується m рівняннями (2), (3) з n = nl + n2 + n3 крайовими умовами, де nl , n2, n3 – відповідно кількості вузлів з умовами (4), (5), (6).
B кожній предметній області є можливість з відповідними припущеннями розглядати мережі як об'єкти з зосередженими параметрами. Так, наприклад, за умови розгляду в певній смузі частот повітряних потоків як нестискуваних маємо в рівнянні (3) і рівняння (2) інтегрується вздовж координати ξ, в межах довжини гілок 1; (0 < ξ < lj):
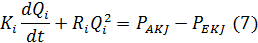
Тут Kі, Ri - відповідно коефіцієнт інерційності потоку та аеродинамічний опір гілки QI.
Крайова умова (4) трансформується в вузлове рівняння, аналогічне першому закону Кірхгофа в електричних мережах для гілок QI, що інциндентні вузлу WJ:
∑QI(WJ)=0 (8)
Введемо вектори потоків Q = (Qi,…, Qm) , характеристик активних елементів H = (Hi(Qi),...,Hm(Qm))1, нелінійних членів z = (Qi2,...,Qm2), топологічні матриці інциденцій A та незалежних замкнутих контурів S, а також діагональні матриці параметрів K, R. Це дає змогу записати рівняння мережного об'єкту матрично-векторній формі [1]:
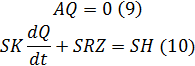
До рівнянь виду (9), (10) можуть додаватись рівняння газодинаміки [2] та багатозв'язної системи керування [2] шахтних вентиляційних мереж, або інші рівняння, характерні для відповідної предметної області.

3. Вимоги до засобів моделювання мережних об'єктів
Аналіз формального опису та досвіду побудови моделей мережних об'єктів [1, 2], можливостей наявних обчислювальних систем та тенденцій розвитку моделюючих середовищ [3] дозволяє сформулювати вимоги, на основі яких повинні розроблятися сучасні та перспективні засоби моделювання цього класу об'єктів:
- повна комп'ютерна підтримка підготовчих робіт з мережними об'єктами (побудова графа, його кодування, запис параметрів та вербальних характеристик гілок, внесення змін);
- автоматизація побудови матриць інциденцій та контурів;
- автоматичне генерування рівнянь для мереж з зосередженими та розподіленими параметрами у формі, що потрібна для чисельного їх вирішення;
- наявність високопотужного вирішувача рівнянь, що забезпечує моделювання як в реальному, так і в прискореному масштабі часу;
- наочна візуалізація етапів побудови моделей мережних об'єктів та результатів моделювання;
- спроможність об'єктів до сумісної роботи з реальною апаратурою контролю та керування потоками в гілках об'єктів;
- доброзичливість засобів моделювання до експертів предметної області, наявність високорозвиненої підсистеми діалогу та засобів навчання користувачів моделей і тренінгу персоналу, що обслуговує мережні об'єкти.
4. Структура моделюючого середовища
Сформульованим вище вимогам відповідає системна організація засобів моделювання у формі паралельного моделюючого середовища, що орієнтоване на вирішення проблеми моделювання мережних об'єктів.
Моделююче середовище, що пропонується, містить у собі дві частини – апаратні та програмні засоби. До апаратних засобів належать обчислювальні системи SIMD та MEMD-архітектур, а також паралельно функціонуючі групи персональних ЕОМ, які називаються кластерами і разом працюють за MIMD-принципом. Структура цих засобів зображена на рис. 2.
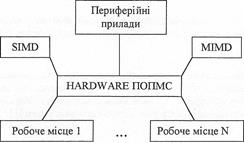
Доступ до апаратних ресурсів виконується за допомогою мережної технології з робочих місць, які базуються на потужних персональних комп'ютерах. Оскільки тут йдеться про паралельне моделююче середовище, то для досягнення високошвидкісного доступу необхідно використовувати комп'ютери тільки цього класу. Для візуалізації й документації результатів моделювання використовуються периферійні прилади. До них відносяться дисплеї, принтери, дигитайзери. Пропонована структура програмних засобів проблемно орієнтованого паралельного моделюючого середовища (ПОПМС) для мережних динамічних об'єктів з зосередженими та з розподіленими параметрами показана на рис. 3.
Усі компоненти ПОПМС мають інтерактивну частину для доступу користувачів та підтримуються за допомогою підсистеми діалогу. Розглянемо основні функції та принципи побудови елементів структури.

5. Топологічний аналізатор
Топологічний аналізатор – це логічно завершена сукупність програм, що реалізують алгоритм побудови дерева і антидерева, а також матриць інциденцій A і незалежних контурів S. Таблиця кодування графа G(m,n) (1) містить всю інформацію, необхідну для побудови цих алгоритмів. Нами запропоновані таблично орієнтовані алгоритми, які перетворюють таблицю (1) в таблиці кодування дерева
NUJ KUJ XID (11)
та антидерева
NUJ KUJ YIAD (12)
в яких відповідно XID – це потоки в гілках дерева (ID=1, 2, n-l), a YIAD – потоки в плках антидерева (IAD=1, 2, у, y=m-n+l). Таким чином, вектор потоків Q графа G(m,n) після побудови дерева і антидерева розбивається на підвектори X і Y:
Q=(X,Y)T (13)
Відповідно структуруються матриці A (Ах Ау) та S (Sx Sy), що будуються із (11), (12), та матриці параметрів і вектор AE.
6. Генератори рівнянь
Генератори рівнянь – це програми, що реалізують алгоритми матрично-векторних операцій приведення системи рівнянь мережних об'єктів у форму, необхідну для чисельного вирішення. Так, для розглянутої вище системи (9), (10) ця форма має вигляд:
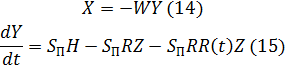
B цих рівняннях матриці
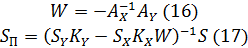
формулюються генератором рівнянь як результат послідовності дій над топологічними матрицями та матрицями параметрів.
Для мережних об'єктів з розподіленими параметрами генерування рівнянь організується в такому порядку:
- з топологічного аналізатора видаються вектори X, Y, матриці Ах, Ау;
- вибирається метод апроксимації рівнянь у часткових похідних системою звичайних диференціальних рівнянь; так, за методом прямих рівняння виду (2), (3) апроксимуються для і-ї гілки графа мережі системою 2M; рівнянь
- відповідно до апроксимації (18), (19) визначаються вектори потоків та тисків в гілках дерева
- формуються матриці параметрів та правила виконання операцій, що формально приводять рівняння кожного елемента мультивекторної системи до форми, що потребують чисельні методи вирішення рівнянь:
- записуються в загальному вигляді крайові умови в вузлах трьох типів: внутрішніх, тих, що виходять в атмосферу та вузлів підключення активних елементів (AE).

де k=l, 2, ... , Mi – номер елемента гілки, Mi – кількість елементів, на які розбивається і-та гілка при апроксимації;
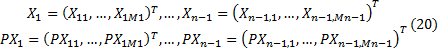
та антидерева
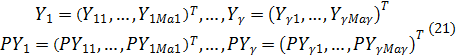
Таким чином, мережний об'єкт з розподіленими параметрами містить мультивектори X, PX, Y, PY, елементи яких у свою чергу мають M та Ma компонентів.
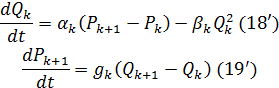
Алгоритми функціонування генератора рівнянь з апроксимацією методом прямих запропоновані та експериментально досліджені в [6]. Алгоритми, що реалізують апроксимацію за методом характеристик та за частотним методом, знаходяться в стадії розробки.
7. Вирішувачі рівнянь
Вирішувачі рівнянь пропонується будувати на основі принципу сумісності ПОПМС з наявними мовами та системами моделювання. Ця сумісність забезпечується використанням об'єктно- (БО) та рівняння-орієнтованих (PO) мов SIMULINK та ACSL, а також чисельних методів, які реалізовані в цих мовах. Мова SIMULINK спроможна використовувати матрично-векторний запис рівнянь, що видається генераторами. Для використання мови ACSL треба представити сформовані рівняння в операторному вигляді.
SIMD-версія паралельних вирішувачів для об'єктів з зосередженими і розподіленими параметрами будується за єдиним методичним підходом:
- матрично-векторні рівняння, що сформовані генераторами, перетворюються в модельні дискретні рівняння, що відповідають вибраному чисельному методу вирішення; при цьому зберігається матрично-векторний запис формул для ітераційних обчислень, який найбільш прийнятний для SIMD-реалізації;
- розробляється програма на SIMD-мові програмування; керування циклами чисельного інтегрування виконує HOST-машина, а паралельні обчислення – поле процесорних елементів (ПЕ) вибраної конфігурації; для об'єктів з зосередженими параметрами всі варіанти матриць та векторів покриваються віртуальною конфігурацією ПЕ розміром m*m (m – кількість гілок графа мережі); віртуальна конфігурація ПЕ для мереж з розподіленими параметрами може будуватися за координатним методом, або за методом з'єднання моделей гілок відповідно до матриці інциденцій A (Ах Ау).
Паралельний MIMD-вирішувач для мереж з зосередженими параметрами може будуватись як за БО-, так і за РО-принципами. Аналіз показує, що ефективне використання паралельності досягається за умови застосування SPMD-організації циклів чисельного вирішення рівнянь мережі.
Матрично-мультивекторне представлення мереж з розподіленими параметрами потребує решітчатої структури MIMD-процесорів та SPMD-організації циклічних програм.
8. Підсистема діалогу
Головним завданням підсистеми діалогу (ПД) є забезпечити доброзичливість моделюючого середовища до розробників та користувачів паралельних моделей складних мережних об'єктів та систем керування ними. ПД має виконувати такі групи функцій:
- Презентацію ПОПМС з графічним зображенням структури ПМС, описом ресурсів ПМС, автоматичним документуванням виконаних експериментів моделювання й наявністю демо-версії моделі мережного об'єкта.
- Навчання користувачів ПМС з таких питань, як: технічні характеристики мереж; топології мереж; рівняння процесів у гілках мережі; структури паралельних моделей; тестові приклади; методи адаптації моделі й ідентифікації мереж; вирішення прикладів вибраних задач; методи візуалізації результатів моделювання.
- Інтерактивне моделювання мережних об'єктів: таблична специфікація мережної топології та введення параметрів, графічне зображення мережі; детальний розгляд фрагментів мережі; використання топологічного аналізатора; візуалізація дерева та антидерева, а також матриць інциденцій та незалежних контурів; перевірка топологічних рішень; генерування та вирішення рівнянь.
- Інтерактивний аналіз моделей: вибір, планування та виконання експериментів моделювання; формулювання необхідних даних моделювання та вихідних функцій; візуалізація, аналіз і документування результатів моделювання; архівація моделей.
9. Імплементація та експериментальні дослідження
Для імплементації SIMD-компонента ПОПМС використано мову паралельного програмування PARALLAXIS, а MIMD-моделей – мову C та стандарт MPI взаємодії паралельних процесів у паралельному середовищі. Були виконані та підтверджені експериментальні дослідження на прикладі малої, середньої та реальної за розмірами шахтних вентиляційних мереж. Є також досвід моделювання електричних мереж.
10. Висновки
Запропоновано проблемну орієнтацію паралельного моделюючого середовища на задачі моделювання мережних об'єктів.
Розроблено структуру апаратних засобів проблемно орієнтованого паралельного моделюючого середовища на сучасних засобах обчислювальної техніки та можливостях доступу до паралельних ресурсів за мережними інформаційними технологіями.
Запропонована структура програмних засобів ПОПМС відповідає особливостям мережних об'єктів як складних систем, вимогам до засобів моделювання систем, забезпечує системний підхід до створення ПОПМС.
Експериментальні дослідження показали [4,5,6,7,8], що ідея побудови проблемно орієнтованих моделюючих середовищ відкриває нові перспективи в галузі моделювання динамічних систем реальної складності. Автори продовжують системну реалізацію ПОПМС для шахтних вентиляційних мереж.
Лiтepaтypa
- Абрамов Ф.А., Фельдман Л.П., Святний BA. Моделирование динамических процессов рудничной аэрологии. – Киев: Наукова думка, 1981.
- Святний B.A. Моделирование аэрогазодинамических процессов и разработка систем управления проветриванием шахт. Докт. дисс., Донецк, ДПИ, 1986.
- Святний B.A. Проблеми паралельного моделювання складних динамічних систем. Наукові праці ДонДТУ, Серія DCOT, вип. 6, 1999, с. 6-14.
- Перерва A.A. Топологический анализатор параллельной модели сетевого обьекта. Наукові праці ДонДТУ, Серія ПСОТ, вип. 6, 1999, с.73-78.
- Перерва A.A. Генератор и решатель уравнений проблемно ориентированной параллельной моделирующей среди для сетевих обьектов с сосредоточенними параметрами. Наукові праці ДонДТУ, Серія "Проблеми моделювання та автоматизації проектування динамічних систем". Випуск 10, 1999, 164-169.
- Святний B.A., Молдованова OB Генератор уравнений параллельной модели сетевого динамического обьекта с распределенними параметрами. Наукові праці ДонДТУ, Серія "Проблеми моделювання та автоматизації проектування динамічних систем". Випуск 10, 1999.
- Перерва A.A. Магістерська дисертація, ДонДТУ, Донецьк, 2000.
- Молдованова O.B. Магістерська дисертація, ДонДТУ, Донецьк, 2000.