Метод нечеткого управления на основе переменных с многомерными функциями принадлежности

Автор: А.Н. Шушура, И.А. Тарасова

Источник: Сборник статей «Искусственный интеллект» [Перейти]

В статье приведено исследование существующих методов нечеткого управления, разработан метод управления на основе нечетких переменных с функциями принадлежности нескольких аргументов, проведено исследование эффективности разработанного метода в задаче управления очисткой воды, выполнен сравнительный анализ результатов работы алгоритмов управления. Применение разработанного метода позволит повысить эффективность нечеткого управления плохо формализуемыми объектами со сложной структурой взаимосвязей входных и выходных переменных. 

 Введение
Одним из наиболее популярных и быстро развивающихся направлений в области современных методов управления плохо формализуемыми объектами является нечеткое моделирование. Вопросам проблематики методологии нечеткого моделирования и технологии решения практических задач посвящены работы: Л. Заде, Э. Мамдани, А.В. Леоненкова, С.Д. Штовбы, А.П. Ротштейна [1-6]. Существующие методы нечеткого управления в основном используют в качестве термов нечеткие переменные с функциями принадлежности одного аргумента. К таким методам относятся Мамдани, Цукамото, Ларсена, Сугено и т.п. [4], [5]. С одной стороны, это позволяет использовать простое и наглядное представление функций принадлежности (например, треугольные или трапециевидные), а также применять несложные вычислительные процедуры при проведении всех этапов нечеткого вывода. С другой стороны, теряется зависимость между управляющими переменными, обусловленная наличием ряда ограничений на управление. Применение для моделирования объектов иерархических систем нечеткого вывода при переходе между уровнями иерархии возникает определенная степень размытости, что может привести к потере значимости результата. Поэтому исследования в области методов нечеткого управления являются актуальными.
    Постановка задачи
Целью данной работы является повышение эффективности управления плохо формализованными объектами за счет разработки метода нечеткого управления, использующего в качестве термов нечеткие переменные с функциями принадлежности нескольких аргументов.
В данной работе решаются следующие задачи:
− разработка метода нечеткого управления на основе нечетких переменных с функциями принадлежности нескольких аргументов;
− проверка эффективности метода на примере конкретного объекта управления и сравнительный анализ результатов его работы с существующими методами.

Разработка метода нечеткого управления на основе нечетких переменных с функциями принадлежности нескольких аргументов

Метод нечеткого управления на основе многомерных функций принадлежности включает в себя следующую последовательность действий:
а) постановка задачи нечеткого управления;
б) формирование термов и их функций принадлежности;
в) формирование базы правил системы нечеткого вывода;
г) фаззификация входных переменных;
д) агрегирование подусловий в нечетких правилах продукций;
е) активизация подзаключений в нечетких правилах продукций;
ж) аккумулирование заключений нечетких правил продукций;
з) дефаззификация выходных переменных.
В рамках постановки задачи определяются входные и выходные переменные объекта управления, на основе входных переменных выбираются управляющие переменные. Выделенные величины представляются в виде лингвистических переменных. Для каждой из лингвистических переменных формируются терм-множества в виде нечетких переменных. Если лингвистическая переменная обладает простой структурой, то для нее могут быть выбраны термы в виде нечетких переменных с одномерной функцией принадлежности. Иначе рекомендуется использовать нечеткие переменные с многомерными функциями принадлежности. Для формирования названий термов и их функций принадлежности могут быть привлечены эксперты. Кроме этого, для определения числа термов и вида их функций принадлежности могут быть использованы методы нечеткого кластерного анализа. В дальнейшем для построения многомерных функций принадлежности в работе используется метод нечетких с-средних [7]. База правил системы нечеткого вывода формируется на основе эмпирических знаний или знаний экспертов в проблемной области и представляется в виде нечетких продукций стандартного вида. Процедура фаззификации заключается в установлении соответствия между конкретным значением i-й входной переменной системы нечеткого вывода и значением 'im b функции принадлежности соответствующего ей терма входной лингвистической переменной, которая в случае многомерных функций рассчитывается по формуле многомерной табличной интерполяции (полиномами Эрмита):

bim = μ m ai , (1)
где ai – значение i-й входной переменной системы нечеткого вывода;
μm(ai ) – функция принадлежности m-го терма.

Агрегирование представляет собой процедуру определения степени истинности условий по каждому из правил системы нечеткого вывода. Если условие правила задано в форме нечетких лингвистических высказываний вида «β есть α», этап их агрегирования оставляет степени истинности без изменения. Если же условие состоит из нескольких подусловий, причем лингвистические переменные в подусловиях попарно не равны друг другу, то определяется степень истинности сложного высказывания на основе известных значений истинности подусловий. При этом для определения результата нечеткой конъюнкции используется формула:

μ (A∧ B) = min{μ (A),μ (B)}, (2)

а для определения результата нечеткой дизъюнкции используется формула:

μ (A∨ B) = min{μ (A) +μ (B),1}. (3)

На этапе агрегирования определяется степень истинности условий bk´´ для каждого к-го правила, входящего в рассматриваемую базу правил системы нечеткого вывода. Это множество значений обозначим через В´´. На этапе активизации для каждой из выходных лингвистических переменных, входящих в отдельные подзаключения правил нечетких продукций, определяются функции принадлежности нечетких множеств их значений. Расчет значения функции принадлежности каждого из подзаключений для рассматриваемых выходных лингвистических переменных осуществляется по формуле:

y) min{с , ( y)} k k μ = μ , (4)

где μ ( y) – функция принадлежности терма, который является значением некоторой выходной переменной; ск – степень истинности каждого из подзаключений, равная алгебраическому произведению соответствующего значения bк´´ на весовой коэффициент правила.
Этап аккумуляции заключается в том, чтобы объединить или аккумулировать с использованием операции max-дизъюнкции все степени истинности заключений для получения функции принадлежности каждой из выходных переменных.
Дефаззификация заключается в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить обычное количественное значение каждой из выходных переменных, которое может быть использовано специальными устройствами, внешними по отношению к системе нечеткого вывода. Для одномерных функций принадлежности применяется стандартный метод центра тяжести. Для многомерного случая используется обобщенный метод центра тяжести:

x j V j ... ' 1 , (5)

где ' 1x … ' n x – результат дефаззификации; V – объем фигуры, образованной функцией принадлежности. Разработанный метод необходимо проверить в задаче управления конкретным объектом.

Исследование эффективности метода нечеткого управления на основе переменных с многомерными функциями принадлежности в задаче управления очисткой воды

С целью установления эффективности разработанного метода нечеткого управления, проведен сравнительный анализ работы данного метода и нечеткого управления на основе алгоритма Мамдани на установке очистки воды. Недостатком существующей организации управления процессом очистки воды является отсутствие контроля качества умягченной воды, что обуславливает актуальность разработки новой системы управления. Поскольку управляющие переменные (параметры дезинфекции) задаются оператором на основе субъективной оценки потока воды, при решении задачи управления целесообразно использовать методы нечеткого моделирования. На основании анализа процесса очистки воды выделены входные и выходные переменные блока нечеткого управления. В качестве входных лингвистических переменных следует использовать:
а) σ – «жесткость воды».
В качестве выходных лингвистических переменных выбраны:
а) β – «способ дезинфекции»;
б) γ – «необходимый поток воды».
Для определения элементов терм-множеств и их функций принадлежности проводится нечеткая кластеризация на основе собранных статистических данных. Присвоив кластерам названия, были получены термы переменных. В качестве терм-множества лингвистической переменной «Жесткость воды» используется множество Т1 = {«минимальная», «нормальная», «максимальная»} с функциями принадлежности, изображенными на рис. 1. В качестве терм-множества лингвистической переменной «Способ дезинфекции» будем использовать множество Т2 = {«интенсивный», «умеренный», «слабый»} с функциями принадлежности, изображенными на рис. 2. В качестве терммножества лингвистической переменной «Поток воды» выбрано множество Т3 = {«максимальный», «нормальный», «слабый»} с функциями принадлежности, изображеннымна рис. 3.

Рисунок 1 – График функции принадлежности для термов лингвистической переменной «Жесткость воды»

Рисунок 2 – График функции принадлежности для термов лингвистической переменной «Способ дезинфекции»

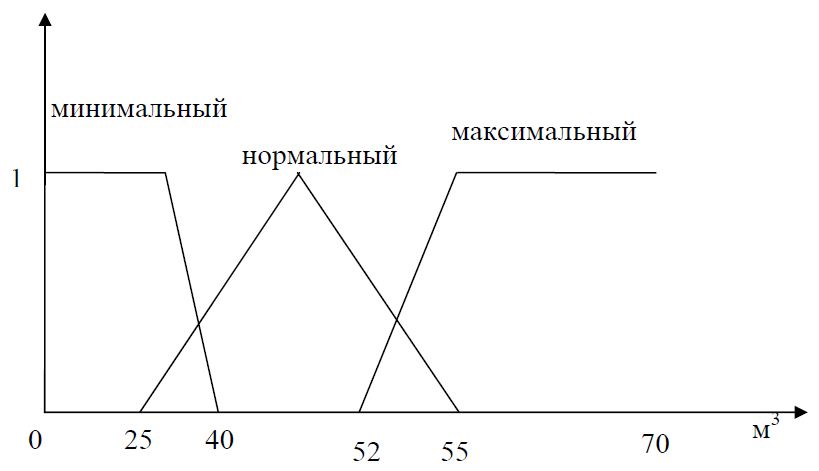
Рисунок 3 – График функции принадлежности для термов лингвистической переменной «Поток воды»

На основании опросов экспертов сформирована база нечетких продукций из трех правил следующего вида:
1. Если «жесткость минимальная», то «поток максимальный» и «способ дезинфекции интенсивный».
2. Если «жесткость нормальная», то «поток нормальный» и «способ дезинфекции умеренный».
3. Если «жесткость максимальная», то «поток минимальный» и «способ дезинфекции слабый».
    Следующим этапом нечеткого вывода является агрегирование подусловий в нечетких правилах продукций. Поскольку все условия правил 1 – 3 заданы в форме нечетких лингвистических высказываний вида «β есть α», этап их агрегирования оставляет степени их истинности без изменения.
    Активизация правил оставляет их степень истинности без изменения, поскольку все заключения правил 1 – 3 заданы в форме нечетких лингвистических высказываний вида «β есть α», а весовые коэффициенты правил равны 1.
    Этап аккумуляции объединяет с использованием операции max-дизъюнкции все степени истинности заключений для получения функции принадлежности каждой из выходных переменных.
    Этап дефаззификации выполняется в соответствии с формулой (5).

Сравнительный анализ результатов работы алгоритмов управления

Численные расчеты по приведенному алгоритму были выполнены в системе MATLAB 6.5. Был проведен сравнительный анализ результатов работы созданного алгоритма с данными, полученными в ходе эксперимента на объекте управления и с помощью стандартного алгоритма Мамдани. Значения управляющих переменных сравнивались со значениями, указанными операторами установки очистки воды. Резуль-
таты сравнения представлены в виде графиков на рис. 4 и 5.

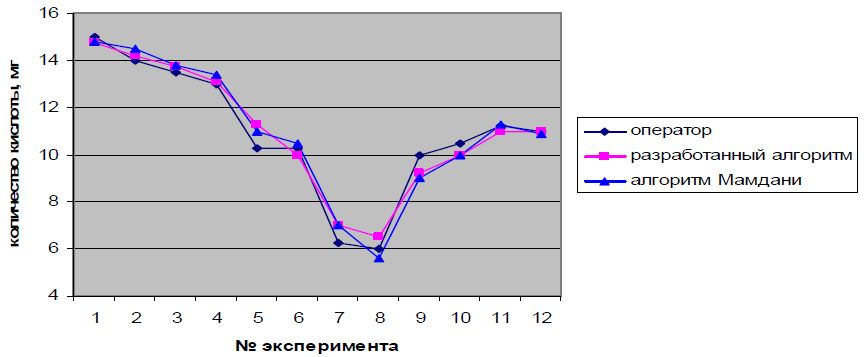
Рисунок 4 – График результата сравнения выходной лингвистической переменной «Количество кислоты»

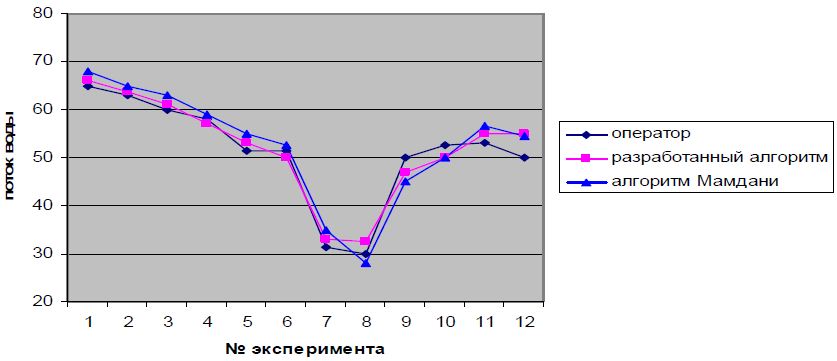
Рисунок 5 – График результата сравнения выходной лингвистической переменной «Поток воды»

Как видно на рис. 4 и 5, алгоритмы нечеткого управления достаточно хорошо описывают принимаемые оператором установки решения, однако алгоритм, использующий многомерные функции принадлежности, обеспечивает более плавный переход из одного состояния в другое, что подтверждает адекватность и эффективность разработанного метода нечеткого управления.

Выводы

В данной работе на основе существующих методов нечеткого управления был разработан новый метод, использующий для задания термов нечеткие переменные с функциями принадлежности нескольких аргументов. В качестве одного из способов задания функций принадлежности нечетких переменных предложено использовать методы нечеткой кластеризации. Данный подход позволяет сохранить в нечеткой модели  правления нелинейные взаимосвязи между переменными объекта. К недостаткам метода следует отнести зависимость результатов его работы от качества решения задачи кластеризации.

Для предложенного метода была проведена проверка его эффективности на примере решения задачи управления процессом очистки воды. Результаты исследования показали эффективность применения предложенных подходов.

Литература: