Назад
в библиотеку
Применение нечеткой логики в имитационной системе автономного
адаптивного управления
Автор: Караваев М.В.
Источник: Журнал: Труды Института
системного программирования РАН [Перейти]
Аннотация. Описан
способ построения автономных адаптивных систем управления на основе
математического аппарата нечеткой логики. Для этой цели было
разработано расширение теории нечётких множеств.
1. Введение
Наиболее продвинутые
на сегодня методы построения автоматических систем управления основаны
на использовании строгих математических моделей объектов. Однако,
для подавляющего большинства как искусственных, так и естественных
объектов управления (ОУ), которыми необходимо управлять, построение
точных математических моделей практически невозможно ввиду их плохой
формализуемости. К тому же, эти объекты могут функционировать в среде,
свойства которой изменяются или же вообще не могут быть определены
заранее. Управление такими объектами возможно только с использованием
адаптивных принципов. В случае плохой формализуемости ОУ особый интерес
вызывают системы, построенные на новых, интеллектуальных принципах [1].
Эти системы используют наработки таких направлений искусственного
интеллекта (ИИ) как нечеткая логика, экспертные системы, генетические
алгоритмы, искусственные нейронные сети и т.д.
Среди всех
интеллектуальных управляющих систем особенно эффективны системы,
построенные не на основе только одного из вышеперечисленных направлений
ИИ, но объединяющие в себе сразу несколько из них.
В данной статье
предлагается один способ объединения двух такого рода методов, именно,
метода ААУ [2,3,4] и нечёткой логики [5,6,7], и построение системы ААУ
на основе модернизированного математического аппарата нечеткой логики,
с целью объединить концептуальность метода ААУ со сравнительной
простотой нечетких систем управления.
Работа поддержана
РФФИ, проекты № 03-01-00323 и№ 04-01 -08023.
Построение
системы ААУ на основе аппарата нечеткой логики позволяет упростить
элементы структуры системы, сохраняя общие принципы метода ААУ, а также
наделяет дискретный по своей сути метод ААУ некоторыми непрерывными
свойствами, что должно повысить качество управления и сократить объем
базы знаний. Нечеткая логика
дает возможность достаточно просто заложить в систему ААУ априорную
информацию об объекте в виде нечетких правил управления, близость формы
записи которых к естественному языку позволяет без особого труда
получать необходимые знания у экспертов. Априорная информация
обеспечивает одно из основных начальных условий системы, построенной по
методу ААУ - условие максимальной начальной приспособленности.
Соблюдение этого условия позволяет получить результат, аналогичный
результату действия механизмов естественного отбора и передачи
наследственной информации, присущих живым организмам.
2. Нечеткая логика
Обработка
нечеткой
информации и нечеткий вывод давно применяются в различных
интеллектуальных системах, однако наиболее широкое распространение
нечеткие системы получили в области управления.
Общая схема
обработки нечеткой информации выглядит следующим образом. Точные
исходные данные с датчиков, контролирующих управляющий процесс,
переводятся в значения лингвистических переменных в специальном блоке,
получившем название “фазификатор”. Далее реализуются
процедуры нечеткого вывода на множестве продукционных правил,
составляющих базу знаний системы управления, в результате чего
формируются выходные лингвистические значения, которые переводятся в
точные значения результатов вычислений в блоке
“дефазификатор”. На выходе последнего формируются
управляющие воздействия подаваемые на исполнительные механизмы. Эта
концептуальная схема лежит в основе так называемого нечеткого
контроллера, используемого в интеллектуальных системах обработки
неопределенной информации, в частности, в
“интеллектуальных” системах управления.
В классических
нечетких регуляторах не предусмотрены механизмы адаптации в реальном
времени к изменяющимся характеристикам взаимодействия объекта
управления с окружающей средой, что не позволяет применять нечеткие
системы для управления объектами с изменяющимся во времени свойствами.
Однако существует ряд методов, расширяющих возможности нечетких
регуляторов в этой области [8].
Одним из
серьёзных недостатков нечетких систем управления является невозможность
предсказания поведения системы на несколько шагов вперед, так как
существующий математический аппарат нечеткой логики позволяет строить
правила управления,
связывающие лишь текущее состояние объекта с желаемым при помощи
управляющего воздействия, которое необходимо предпринять в текущей
ситуации.
3. Математический аппарат нечеткой
логики для систем ААУ
Одни из основных
задач, которые необходимо решить при построении системы ААУ -задача
получения и представления в базе знаний (БЗ) эмпирической информации и
задача принятия решений на основе найденных в этих знаниях
закономерностей. Под БЗ в системах ААУ понимается подсистема, хранящая
знания, необходимые системе ААУ для управления объектом, где
«знания» для системы ААУ представляют собой тройки
«образ ситуации»-«образ действия»-«образ
результата», отражающие закономерности во взаимодействиях объекта
управления с окружающей средой. Исходя из вышесказанного, существует
возможность построения управляющей системы ААУ с использованием
математического аппарата нечеткой логики, которая чаще всего
применяется как раз для решения подобных задач. При этом в
разрабатываемой системе необходимо объединить концептуальность метода
ААУ и сравнительную простоту нечетких систем управления.
Для описания
системы ААУ мы предлагаем использовать нечеткие и лингвистические
переменные, имеющие некоторые отличия от принятых в традиционной
нечеткой логике.

Рис. 1.
Графическое представление функций принадлежности нечетких переменных.
Нечеткая
переменная, используемая в системе, характеризуется множеством: V = {Н,
Р}, где Н - наименование нечеткой переменной, совпадающее с номером
интервала (нечеткого
множества) из диапазона значений физической переменной (рисунок 1), а Р
-значение степени принадлежности физической переменной нечеткому
множеству, соответствующему этому диапазону.
Лингвистическая
переменная в системе представлена набором 2 = {У 1, , Умо, Ц, где У],
...,
Умо -
значения
нечетких переменных, а Ь - уровень детализации лингвистической
переменной, численно равный количеству интервалов, на которые
разбивается диапазон значений физической переменной. Значение константы
М0 равно максимальному числу нечетких переменных, входящих в
терм-множество этой лингвистической переменной, значение функций
принадлежности для которых одновременно может принимать значения
большие нуля. Значение М0 полностью определяется видом функции
принадлежности: для линейной и квадратичной функций М0 принимает
значение 2, для обратной квадратичной Мо равно 4.
Нечеткий
образ
характеризуется набором О = /2/, Е}, где - значения лингвистических
переменных системы, количество которых определяется константой N0, а Е
- значение оценки данного образа, вычисляемое по формуле на рисунке 1:
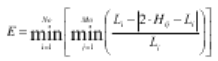 (1)
(1)
Такой вид формулы
следует из предположения, что область с максимальной оценкой находится
в центре диапазона значений любой физической переменной и большую
оценку имеет та нечеткая переменная, которая находится ближе всех к
середине диапазона с любой стороны от нее.
Для образа
состояния объекта управления оценка Е означает близость образа к
состоянию ОУ с минимальными отклонениями от заданных значений всех
входных переменных. Для образа управляющего воздействия оценка
характеризует, например, энергозатраты исполняющего органа при
выполнении управляющего действия: значение выходной физической
переменной, близкое к центру диапазона значений, означает отсутствие
управляющего действия.
Пусть
«память истории управления» состоит из образов текущего
состояния ОУ и управляющего воздействия О а, и имеет вид конечной
последовательности:
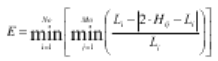 , (2)
, (2)
где Н, -
количество образов в памяти истории управления.
Применительно к
модели управляющей системы стабилизации углового движения космического
аппарата “Пилот”, подробно описанной в [2], в образ
текущего состояния входят две
лингвистические переменные: “угловое отклонение” и
“угловая скорость”, а в образ управляющего воздействия Ом -
лингвистическая переменная “выходное воздействие”.
Для модели
управляющей системы “Пилот” история управления в терминах
нечетких переменных будет выглядеть следующим образом (здесь Мо=2, Мо=2
для линейной функции принадлежности):

Вид нечетких
правил управления, используемых в системе, также отличается от
традиционного: традиционное правило управления является лишь частью
правила модернизированного
аппарата нечеткой логики, определяющей управление объектом только на
одном такте. Выраженное в лингвистической форме, правило управления
системы “Пилот” будет выглядеть следующим образом:
если Zsi есть Vsu
И Zs2 есть Vsi2, то Za есть Vai —> если Zsi есть Vs2iH Zsi
есть Vs22, то Za есть Va2 —>... —> если Zsi есть Vsu
И Zs2 есть Vs,2, то Za есть Vai где Zsi, ZS2 и ZA
- значения входных лингвистических переменных “угловое
отклонение” и “угловая скорость” и выходной
“управляющее воздействие”, Vsu, Vs/2 и Vai - конкретные
значения нечетких переменных, с которыми происходит сопоставление
значений Zsi, Zs2 и Za-
На уровне
нечетких переменных правила управления хранятся в виде
последовательности:
{{Hsu , РSil ,
Lsil}, {Hsi2 , РSi2 , LSi2}, Щм, LAi}} —»..., (3)
где Hsu и HSi2 -
наименования входных нечётких переменных; PSil и PSi2 - степени
значимости данных нечётких переменных в г-ом элементе правила; Lsa и
Lsu - уровень детализации лингвистических переменных, в терм-множества
которых входят эти нечеткие переменные, Hai и Lai - наименование и
уровень детализации выходной нечеткой переменной.
Степень
значимости PSi нечёткой переменной в г-ом элементе правила вычисляется
как среднее значение степеней принадлежности входных физических
переменньк нечётким переменным соответствующего образа при формировании
правила из повторяющихся фрагментов истории управления. Этот принцип в
некоторой степени соответствует назначению веса синапса в искусственных
нейронных сетях, определяющему влияние значений входных и промежуточных
переменных на результат, а также соответствует коэффициенту посылки в
экспертных системах.
Работа элементов
правил определяется минимаксной композицией (1).
Выходное
управляющее воздействие может вычисляться в соответствии с формулой
нахождения средневзвешенной величины:
где а* - выходные
воздействия правил, Р* - степени принадлежности выходного управляющего
воздействия нечеткой переменной, задаваемой этим правилом, или по
методу центра тяжести:
формула для
которого применительно к линейной функции принадлежности принимает вид:
Возможен вариант
управления, при котором среди сработавших элементов правил выбирается
одно правило с максимальным результатом и выполняется действие,
заданное этим элементом.
4. Структура и
основные принципы работы системы ААУ на основе нечеткой логики
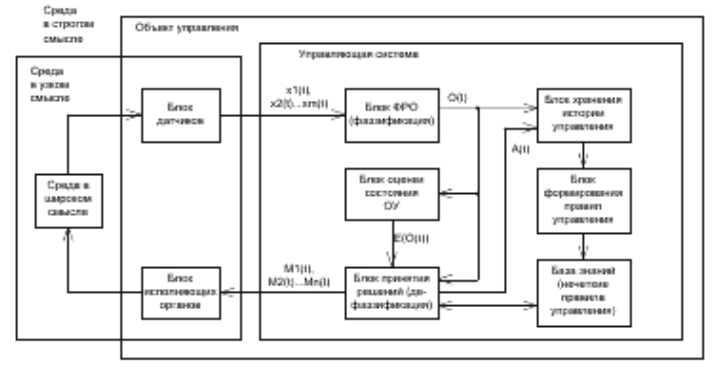
Общая структура
системы, основные блоки которой с некоторыми изменениями заимствованы
из базовой системы ААУ[2,3,4], изображена на рисунке 2.
Система
состоит
из следующих модулей: блока датчиков, блока формирования и
распознавания образов, блока памяти истории управления, блока
формирования правил управления, блока оценки состояния объекта
управления, базы знаний нечетких правил управления, блока принятия
решений и исполняющего органа, а также окружающей среды. Здесь под
средой в широком смысле понимается вся внешняя среда, на которую может
оказывать воздействие исполняющий орган и параметры которой может
регистрировать блок датчиков, включая сам объект управления. Под средой
в узком смысле понимается внешняя среда без ОУ.
Под базой
знаний
системы в дальнейшем подразумевается совокупность памяти истории
управления и набора нечетких правил управления. Последний также можно
назвать базой знаний правил управления.
Блок
датчиков
через равные интервалы времени (на каждом такте работы управляющей
системы) измеряет параметры внешней среды, например для спутника:
угловое отклонение и угловую скорость. Они в виде значений физических
переменных х\ф, хг(0,... хпф поступают на вход блока формирования и
распознавания образов.
Рис. 2. Общая
структура системы ААУ с использованием нечеткой логики.
Блок ФРО
производит сопоставление входных физических переменных Х\ф,
х2ф,... хпф, нечётким множествам соответствующих нечетких переменных
(фазификация) -
вычисление для
каждой нечеткой переменной значения характеристической
функции принадлежности.
Далее происходит
формирование образа текущего состояния объекта управления в
соответствии с текущим уровнем детализации /,/, каждой г-ой входной
лингвистической переменной. Изначально каждая входная физическая
переменная сопоставляется, например, только с тремя входными нечёткими
переменными: /,/, = 3. При накоплении определённого количества знаний
для повышения качества управления часто возникает необходимость в более
точном измерении какого-либо входного параметра. Тогда диапазон
значений соответствующей входной физической переменной разбивается на
большее число интервалов, например, на Ы,+2, и система начинает
оперировать уже 5-ю нечёткими переменными вместо 3-х и т.д..
Затем
сформированный нечеткий образ поступает на вход блока оценки состояния
объекта управления, который вычисляет для этого образа оценку по
формуле (1).
Блок
хранения
истории управления сохраняет конечную последовательность образов
состояний объекта и управляющих воздействий в виде (2). Причём для
соблюдения условия дискретности память истории управления может хранить
информацию, полученную только на последних Мр тактах управления, а все
сведения о состоянии объекта на тактах управления, отстоящих от
текущего момента времени более чем на Мр тактов - утрачиваются
(“забываются”). Величина Мр влияет на качество формируемых
правил управления и задается априорно, исходя из предполагаемого
периода повторения характерных для системы закономерностей во входных и
выходных данных. Обобщенная информация о более ранних событиях в
истории управления может сохраниться в базе знаний нечетких правил
управления, если она еще не потеряла своей актуальности.
Блок
формирования
правил управления обеспечивает один из аспектов адаптивности
разрабатываемой системы: динамическое формирование нечетких правил
управления. Он работает следующим образом. Через определенное число
тактов просматривается история управления и производится поиск
повторяющихся фрагментов. Далее из этих участков формируется правило
управления при соблюдении следующих обязательных условий:
а) все суммы
степеней принадлежностей входных переменных нечётким
множествам повторяющегося участка превышают некоторый порог Ра;
б) последним
результирующим образом этого участка истории является
образ с максимальной оценкой для текущего уровня детализации;
в) среднее
качество управления (средняя оценка образов) на данном
отрезке превышает порог Еа,
г) общие затраты
энергии исполнительным органом на данном участке
истории не превышают величину й7,,;
д) длина данного
фрагмента не превышает некоторую априорно задаваемую
величину ыа.
При несоблюдении
последнего условия от отрезка истории отсекается начальная его часть
необходимой для выполнения этого условия длины. Однако при этом может
перестать выполняться третье условие.
При
формировании
двух или более противоречащих друг другу правил в базу знаний заносится
правило, имеющее наибольшее среднее качество управления и наименьшие
энергозатраты исполняющего органа. В зависимости от конкретной задачи
разрабатываемой системы управления критерий выбора оптимального правила
может варьироваться.
Противоречивыми
правилами считаются правила, значения лингвистических переменных первых
образов которых полностью совпадают, за исключением степени
уверенности.
Набор правил
управления в какой-либо точке пространства входных переменных считается
точечно-полным, если в этой точке средняя степень принадлежности
значений всех физических переменных входным множествам нечетких правил
превышает некоторую априорно задаваемую величину Р„. Набор правил
управления считается полным, если среднее значение степеней
принадлежности превосходит Рг во всех точках пространства входных
признаков.
Если на
каком-то
такте при текущих значениях входных переменных в соответствующей точке
пространства условие полноты правил управления не выполняется, то при
вычислении выходного управляющего воздействия сумма степеней
принадлежности выходных нечётких переменных дополняется до значения Рг
случайной величиной, тяготеющей к нулевому воздействию. Таким образом
происходит обучение системы управления при недостатке в базе знаний
эмпирической информации в виде нечетких правил.
Помимо
динамического формирования правил управления, свойства адаптивности
системы стабилизации обеспечиваются механизмом удаления неадекватных
текущим условиям правил: у каждого правила управления имеется счётчик
сбоев, который увеличивается на единицу при каждом срабатывании
правила, не приведшем к ожидаемому результату (образу с максимальной
оценкой). После хотя бы одного удачного выполнения правила счётчик
сбрасывается. Превышение счётчиком некоторой априорно задаваемой
величины С* говорит об изменении свойств объекта или внешней среды,
после чего данное правило нельзя больше использовать для управления
объектом. В этом случае правило удаляется из базы знаний.
При
превышении
степеней принадлежности всех нечётких переменных распознанного образа
какого-либо правила порогового значения Р„ задаваемого априорно,
примем, что ситуация управления развивается по данному правилу. Примем
также, что правило сработало, если это условие выполнялось в течение
определенного количества тактов, равного половине длины правила. Если
существует несколько правил, для которых выполняется условие, то в
рассмотрение попадает каждое из них. Если на последующем такте
управления суммарная степень принадлежности нечётким переменным
становится
ниже порога
Рг,
то данное правило выпадает из рассмотрения. Но если при этом отношение
8ит(Р^/Мг (где - количество образов(тактов управления) входящих в
правило) превышает априорно задаваемую величину Ря то считается, что
это правило сработало с отрицательным результатом и значение счётчика
сбоев этого правила увеличивается на единицу.
Если при
формировании нового правила в базе знаний отсутствует место для его
сохранения, то из набора существующих правил могут быть удалены правила
в соответствии со следующими критериями (в порядке убывания
значимости): с наибольшим значением счетчика сбоев, наименьшим средним
качеством управления, наибольшей длиной и энергозатратами.
Блок принятия решений
вычисляет степени принадлежности значений выходных воздействий выходных
нечётких переменных каждого правила в соответствии с основными
операциями над нечёткими множествами, подставляя в посылки правил
степени принадлежности входных переменных соответствующих нечётким
образам. Далее по вычисленным степеням принадлежности находится
значение выходного воздействия в соответствии с формулой (4) или (5).
В процессе
управления используются все правила, находящиеся в базе знаний. При
этом правила, нечеткие переменные которых имеют отличный от текущего
уровень детализации, влияют на результирующее выходное воздействие с
некоторым поправочным коэффициентом, равным Ьр / Li , где Li - значение
текущего уровня детализации г-ой лингвистической переменной, а Ьр -
уровень детализации соответствующей нечеткой переменной_/-ого правила
управления.
Уровень
детализации вычисления выходного управляющего воздействия может
поддерживаться на уровне округленного в большую сторону среднего
значения уровней детализации всех входных лингвистических переменных.
Увеличение
общего
уровня детализации происходит при достижении полноты системы правил
управления, в то время как среднее качество управления не превышает
некоторой априорно заданной величины Е„.
Повышение
уровня
детализации одной из входных лингвистических переменных производится
также при нахождении двух повторяющихся последовательностей образов в
истории управления, в которых одно и то же управляющее воздействие при
одних и тех же начальных условиях приводит к переходу объекта
управления в различные состояния. Причем эти состояния отличаются друг
от друга именно значением этой лингвистической переменной.
Исполняющий орган
выполняет управляющие воздействия Мф, пытаясь изменить тем самым
параметры внешней среды по отношению к объекту управления.
5. Практическая
реализация системы ААУ с элементами нечеткой логики
На основе
модернизированного метода ААУ были построены две программные модели для
управления угловым движением автоматического космического аппарата и
для управления активной автомобильной подвеской.
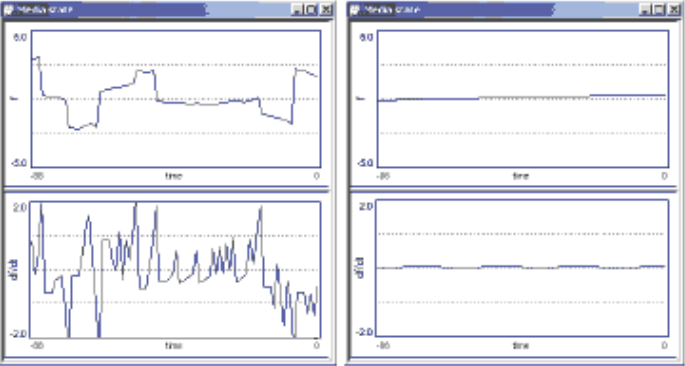
На рисунке 3
изображены графики зависимостей углового отклонения и угловой скорости
корпуса космического аппарата от времени на начальном этапе управления
с использованием нечеткой логики (б) и без нее (а). Такое преимущество
было достигнуто за счет внесения в систему априорных знаний.
Рис. 3. Сравнение
качества управления на начальном этапе работы адаптивной системы
управления с использованием нечеткой логики (б) и без нее (а).
Помимо сокращения
времени обучения на начальном этапе, построение системы ААУ на нечетких
принципах позволило примерно в 4 раза сократить объем базы знаний при
сохранении высокого качества управления (5*5 образов против 11*11
образов в эталонной версии системы “Пилот”).
При испытании
программной модели было также определено, что оптимальной для системы
“Пилот” является линейная (треугольная) функция
принадлежности входных физических переменных нечетким множествам, к
тому же, она наиболее проста для вычисления, а так же то, что
оптимальный вариант объединения выходных результатов сработавших правил
- по среднему значению.
Аналогичные
результаты были получены и при испытании программной модели
управления активной подвеской автомобиля.
6. Заключение и направления дальнейших
исследований
Основной результат
представленной работы состоит в том, что был
расширен математический аппарат нечеткой логики, это позволило
использовать нечеткую логику в системах ААУ. В частности:
а) разработана
структура системы ААУ и ее формальное описание с
использованием математического аппарата нечеткой логики;
б) разработаны
алгоритмы работы системы и основных ее блоков на основе
нечеткой логики: именно, блока принятия решений и блока формирования
правил управления;
в) определена
структура базы знаний, состоящая из памяти истории
управления и набора нечетких правил управления;
По отношению к
базовой версии системы ААУ, предлагаемая система
обладает следующими преимуществами:
а) новая система
имеет в 2-4 раза меньший объем базы знаний при
одинаковом качестве управления;
б) использование
математического аппарата нечеткой логики позволяет вводить в систему
правила управления, полученные на основании априорных знаний экспертов,
и выраженные в форме, близкой к естественному языку. Этим значительно
повышается качество управления на начальном этапе работы системы и
сокращается время самообучения;
в) система
способна автоматически определять необходимую для заданного качества
управления точность представления входных и выходных данных.
В ходе дальнейших
исследований предполагается разработать формальную модель нейрона с
использованием математического аппарата нечеткой логики, тем самым
приблизив функциональные свойства модели нейрона к его биологическому
оригиналу.
Правила нечеткой
логики могут быть использованы для построения структуры нейроноподобной
сети. В процессе исследований предполагается разработать метод
формирования таких правил путем анализа эмпирической информации,
накопленной объектом управления на начальном этапе своего
функционирования, а также методы объединения и минимизации нечетких
правил с целью оптимизации структуры управляющей системы. Для целей
оптимизации могут быть применены различные методы логического вывода,
используемые в булевой алгебре и логике предикатов, адаптированные к
нечеткой логике.
Развитие
различных методов оптимизации базы знаний должно открыть возможности
построения знаний над знаниями, получения нечетких правил (образов)
более высокого порядка, что может перевести исследования на новый
уровень - к построению иерархических управляющих систем.
В дальнейшем
предполагается разработка практических приложений модернизированной
системы ААУ - программных моделей систем управления различными
объектами, например, роботом или автомобильной подвеской.
Список литературы
1. Захаров В.Н.
Современная информационная технология в системах
управления. -Известия академии наук. Теория и системы управления №1,
2000, - с. 70-78.
2. Жданов
А.А. Об одной методологии автономного адаптивного управления.
-Труды института системного программирования, 1999. Том 1. Под ред.
Иванникова В. П. М.: Бионформсервис, 2000. - с.66-83.
3. Жданов
А.А. Метод автономного адаптивного управления. - Известия
академии наук. Теория и системы управления №5, 1999, - с. 127-134.
4. Zhdanov
A. A., Vinokurov А. N.. Emotions Simulation in Methodology
of Autonomous Adaptive Control. Proceedings of ISIC'99/ISAS'99. 1999.
5. Заде
JI.A. Понятие лингвистической переменной и его применение к
принятию приближенных решений. М.:Мир, 1976.
6. Пивкин
В.Я., Бакулин Е.П., Кореньков Д.И. Нечеткие множества в
системах управления, http://idisys.iae.nsk.su/fuzzy_book/
7. Баер П.,
Новак С., Винклер Р. Введение в нечеткую логику и системы
нечеткого управления, http://softlab.od.ua/algo/neuro/fuzzv-intro/
8. Бураков
М.В. Механизм адаптации нечёткого регулятора. - Известия
академии наук. Теория и системы управления №1, 1998, - с. 84-87.

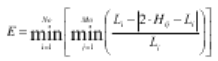 (1)
(1) 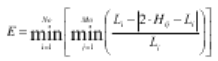 , (2)
, (2)