УДК 621.311.45
ПРИМЕНЕНИЕ НЕЧЕТКОЙ
ЛОГИКИ ДЛЯ СОГЛАСОВАНИЯ РЕЖИМОВ РАБОТЫ ВЕТРОЭНЕРГЕТИЧЕСКОЙ УСТАНОВКИ С
ГРАФИКОМ ЭЛЕКТРИЧЕСКОЙ НАГРУЗКИ
В.З.
Манусов, А.В. Седельников
Источник: Журнал: Известия Томского политехнического университета [Перейти]
Новосибирский
государственный технический университет Е-mail:
Manusov@merlin.power.nstu.ru
Предлагается
методика расчета, учитывающая фактор неопределенности силы ветра, как
энергоносителя, являющегося случайным неуправляемым природным
процессом, а также предложен системный подход для согласования
ветоэнергетических ресурсов с графиком нагрузки и возможности
аккумулирования энергии. Принцип оценки ветроиспользования основан на
теории нечетких множеств.
Введение
Важнейшим
условием повышения техникоэкономических показателей ветроэнергетических
установок (ВЭУ) является наиболее строгое соответствие характеристик
агрегата ветровому режиму
- с одной
стороны, и с другой - особенностям электропотребителя. В этом смысле
главным является нахождение оптимальных расчетных скоростей ветра,
определяющих установленную мощность, и скорости потока, при которой
вступает в действие система автоматического регулирования,
ограничивающая развиваемую ветроколесом мощность. Расчеты балансов
поступления энергии от ветроустановки и ее расхода (потребления) за
любой период или в любой момент времени являются важнейшей процедурой,
позволяющей определить большинство аспектов, характеризующих
эффективность ветроиспользования.
Ветроэнергетический
агрегат работает по неуправляемому графику, потребитель же часто не
допускает перебоев в подаче энергии или продукта
переработки,
требует обеспечения его энергией по заданному графику нагрузки [1, 2].
Нечёткая
логика наиболее хорошо подходит для решения задач оценки ситуации
управления и принятия решений в условиях неопределённости, в тех
случаях, когда человеком не могут быть даны точные количественные
оценки того или иного параметра, а также, когда нахождение точного
решения стандартными методами связано с большими временными,
вычислительными затратами, либо требуют для своей реализации больших
объёмов памяти. В связи с этим предполагается перспективным применение
нечёткого анализа в области ветроэнергетики.
1. Нечеткие
переменные
Представим
шкалу Бофорта (табл. 1) характерными функциями принадлежности
лингвистических переменных ветра [3]: для пограничных интервальных
значений скоростей ветра каждой характеристики ^=0,5. При ^=1 значение
скорости в каждом диапазоне будет равна (^^^/2.
Таблица 1.
Нечеткая характеристика силы ветра
| Скорость ветра, м/с |
Принадлежность, отн. ед |
Характеристика силы ветра |
| 1,8 |
0,5 |
Легкий |
| 2,7 |
1 |
| 3,6 |
0,5 |
| 4,7 |
0,5 |
Слабый |
| 5,8 |
1 |
| 5,8 |
0,5 |
| 7,15 |
0,5 |
Умеренный |
| 8,5 |
1 |
| 8,5 |
0,5 |
| 9,75 |
0,5 |
Свежий |
| 11 |
1 |
| 11 |
0,5 |
| 12,5 |
0,5 |
Сильный |
| 14 |
1 |
| 14 |
0,5 |
| 15,5 |
0,5 |
Крепкий |
| 17 |
1 |
| 17 |
0,5 |
| 19 |
0,5 |
Очень крепкий |
| 21 |
1 |
| 22 |
0,5 |
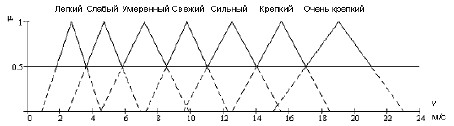
При рассмотрении
функции принадлежности скорости ветра (рис. 1), необходимо учитывать
принадлежность на интервале от 0 до 1. Поэтому достроим каждое значение
нечеткой переменной, основание которой будет иметь значение ^=0, и для
наглядности расчетов сделаем сечения в нескольких точках значений
^=(0...1), где каждое сечение будет характеризовать уровень
принадлежности а] (рис. 2), гдеу=0; 0,25; 0,5; 0,75; 1.
Рис. 1. Нечеткие
значения ветра
Рис. 2. Характеристика
нечетких значений ветра на полном интервале принадлежности
Соответственно, для
ветроустановки, технические характеристики которой указаны в табл. 2,
найдем значения вырабатываемой мощности, с учетом всех уровней
принадлежности. При скорости ветра и0 и плотности воздуха р
ветроколесо, ометающее площадь А, развивает мощность:
Здесь Ср - параметр,
характеризующий эффективность использования ветроколесом энергии
ветрового потока и называемый коэффициентом
мощности.
Коэффициент мощности Ср зависит от конструкции ветроколеса и скорости
ветра. Найденные значения вырабатываемой мощности сведем в табл. 3.
Технические
характеристики ВЭУ
Таблица 2 - Технические характеристики ВЭУ
| Номинальная мощность,
P, кВт |
1000 |
| Диаметр ветроколеса,
D, м |
35 |
| Число лопастей, k, шт. |
3 |
| Коэффициент мощности,
Ср |
0,38 |
| Частота вращения,
nmin/nmax, об/мин |
40 |
| Диапазон рабочих
скоростей ветра, U0, м/с, min; nom; max |
5,5; 17; 25 |
| Номинальное
напряжение, U„, кВ |
10 |
Номинальная частота,
f, Гц |
50 |
| Площадь ометаемой
поверхности, А, м2 |
963 |
| Высота установки
гондолы ВЭУ, H, м |
40 |
| Тип генератора |
АГ |
Зависимость вырабатываемой мощности от
скорости ветра
| Уровень
принадлежности, отн. ед. |
Скорость ветра, м/с |
Характеристика
скорости ветра |
Значения
мощности ВЭУ, кВт |
Характеристика
мощности ВЭУ |
| 0 |
0,9 |
4,5 |
Легкий |
0,146 |
18,31 |
Очень малая |
| 0,25 |
1,35 |
4,05 |
0,494 |
13,35 |
| 0,5 |
1,8 |
3,6 |
1,172 |
9,377 |
0,75 |
2,25 |
3,15 |
2,289 |
6,282 |
| 1 |
2,7 |
3,956 |
3,956 |
| 0 |
2,5 |
6,9 |
Слабый |
3,140 |
66,03 |
Малая |
| 0,25 |
3,05 |
6,35 |
5,702 |
51,46 |
| 0,5 |
3,6 |
5,8 |
9,377 |
39,21 |
| 0,75 |
4,15 |
5,25 |
14,36 |
29,08 |
| 1 4 |
4,7 |
20,36 |
20,86 |
| 0 |
4,45 |
9,85 |
Умеренный |
17,,71 |
192,0 |
Средняя |
| 0,25 |
5,13 |
9,18 |
27,13 |
155,4 |
| 0,5 |
5,18 |
8,5 |
39,21 |
123,4 |
| 0,75 |
6,48 |
7,83 |
54,69 |
96,48 |
| 1 |
7,15 |
73,47 |
73,47 |
| 0 |
7,25 |
12,25 |
Свежий |
76,59 |
369,4 |
Больше
среднего |
| 0,25 |
7,88 |
11,63 |
98,35 |
316,1 |
| 0,5 |
8,5 |
11 |
123,4 |
267,5 |
| 0,75 |
9,13 |
10,38 |
152,9 |
224,7 |
| 1 |
9,75 |
186,2 |
186,2 |
| 0 |
9,5 |
15,5 |
Сильный |
172,3 |
748,4 |
Большая |
| 0,25 |
10,25 |
14,75 |
216,4 |
645,0 |
| 0,5 |
11 |
14 |
267,5 |
551,5 |
| 0,75 |
11,75 |
13,25 |
326,0 |
467,5 |
| 1 |
12,5 |
392,5 |
392,5 |
| 0 |
12,5 |
18,5 |
Крепкий |
392,5 |
1000 |
Очень
большая |
| 0,25 |
13,25 |
17,75 |
467,5 |
1000 |
| 0,5 |
14 |
17 |
551,5 |
987,5 |
| 0,75 |
14,75 |
15,25 |
645,0 |
862,4 |
| 1 |
15,5 |
748,4 |
748,4 |
| 0 |
15 |
23 |
Очень
крепкий |
678,3 |
1000 |
Максимальная |
| 0,25 |
16 |
22 |
823,2 |
1000 |
| 0,5 |
17 |
21 |
987,5 |
1000 |
| 0,75 |
18 |
20 |
1000 |
1000 |
| 1 |
19 |
1000 |
1000 |
2. Анализ
режимов работы ВЭУ
В основу
анализа режима работы ВЭУ в нечетко
-
определенных условиях положен принцип построения нечеткой модели,
основанной на бинарных и условных нечетких отношениях [4, 5]. Первое из
этих нечетких отношений строится на двух базисных множествах X и Y, а
второе - на двух базисных множествах Y и Z. Здесь X - описывает
множество характеристик силы ветра, взятые по шкале Бофорта, Y -
множество характеристик вырабатываемой мощности, а Z - множество
суточных интервалов нагрузки. Нечеткое отношение L - описывает
выработку мощности ВЭУ при определенном ветре, а N - покрытие суточного
графика нагрузки.
Пусть Х={хь
Х2, Хз, Х4, х5, x„, X7}, Y={yb у2, y}, У4, у5, y6, у7} и Z={zi,
z2, z3, z4, z5, z6}. Элементы универсумов имеют следующий
содержательный смысл:
1. x1 -
“легкий”, х2 - “слабый”, х3 -
“умеренный”, х4 - “свежий”, х5 -
“сильный”, х6 - “крепкий”, х7 - “очень
крепкий”.
2. y1 -
“очень малая”, у2 - “малая”, у3 -
“средняя”, у4 - “больше среднего”, у5 -
“большая”, у6 - “очень большая”, у7 -
“максимальная”.
3. zi -
“0-4 ч”, Z2 - “4-8 ч”, Z3 - “8-12
ч”, Z4 -“12-16 ч”, z5 - “16-20 ч”, z6 -
“20-24 ч”.
В качестве
исходных данных принят график нагрузки (рис. 3), значение мощности
указано в кВт.
Рис. 3. Гоафик
нагрузки
Для
построения нечеткого отношения N покрытия суточного графика нагрузки
(табл. 4) можно воспользоваться понятием условного нечеткого
подмножества [5]. Тогда отношение, задающее нечеткое подмножество
определится как л(<уг,^>)=тах(тт(л(у//г), л(у)).
Нечеткое отношение N
покрытия суточного графика нагрузки, отн. ед.
Нагрузка
Покрытие суточного графика нагрузки
0-4
4-8 8-12 12-16 16-20 20-24
Очень малая 0,067
0,033 0,016 0,019 0,013 0,033
Малая 0,25 0,128 0,064
0,073 0,051 0,128
Средняя 0,5 0,308
0,194 0,222 0,155 0,308
Больше среднего 0,931
0,562 0,334 0,382 0,267 0,562
Большая 1 0,981 0,584
0,668 0,5 0,981
Очень большая 1 1
0,935 1 0,75 1
Максимальная 1 1 1 1 1
1
Рассмотрим,
каким образом получено одно из значений принадлежности, например первое
значение /ц(<у1гг1>)=0,067. Вначале, для каждого уровня
принадлежности а рассчитываем отношения мощности ВЭУ к мощности
нагрузки (мощность нагрузки на интервале 0-4 (рис. 3) равна 200
кВт):Рвэу/200.
Распределение мощности ветроустановки, отн.
ед.
Уровень
принадлежности Значение мощности ВЭУ, кВт Покрытие графика нагрузки
0 0,146
18,31 0,0007 0,0915
0,25 0,494 13,35
0,0024 0,067
0,5 1,172 9,377 0,0058
0,0468
0,75 2,289 6,282
0,0114 0,0314
1,0 3,956 3,956 0,0197
0,0197
Находим
минимальные значения принадлежности, а именно тт{0, 0,0007}=0, тт{0,25,
0,0024}=0,0024, тт{0,5, 0,0058}=0,0058, тт{0,75, 0,0114}=0,0114, тт{1,
0,0197}=0,0197, тш{0, 0,0915}=0, тт{0,25, 0,0667}=0,067, тт{0,5,
0,0468}=0,0468, тт{0,75, 0,0314}=0,0314.
Затем,
максимальное значение из полученных будет являться искомым значением
принадлежности л(?). л(г)=тах {0, 0,0024, 0,0058, 0,0114, 0,0197, 0,
0,067, 0,0468, 0,0314}=0,067.
Для
построения нечеткого отношения Ь выработки мощности ВЭУ при заданной
скорости ветра, отношение, задающее нечеткое подмножество определится
как л(<у;,^>)=тах(т1п(л(у//г), л(у)), табл. 5. Процедура
построения матрицы нечетких отношений аналогична предыдущей, за
исключением того, что характеристика мощности ветра задана функцией
принадлежности, которая соответственно зависит от функции
принадлежности скорости ветра. Поэтому для каждого уровня
принадлежности а, при построении искомой матрицы, необходимо учитывать
каждое нечеткое значение мощности ВЭУ.
Отношение выработки
мощности ВЭУ, отн. ед.
Ветер Очень
малая Ма- лая Сред- няя Больше сред- него Боль- шая Очень боль- шая
Макс.
Легкий 1
0,250 0,085 0,042 0,020 0,013 0,013
Слабый 1 1 0,317 0,162
0,079 0,051 0,051
Умеренный 1 1 1 0,461
0,241 0,155 0,155
Свежий 1 1 1 1 0,485
0,271 0,267
Сильный 1 1 1 1 1
0,542 0,500
Крепкий 1 1 1 1 1 1
0,750
Очень крепкий 1 1 1 1
1 1 1
Результат
операции нечеткой композиции отношений табл. 5 и 6 может быть
представлен в виде нечеткого отношения табл. 7:
Покрытие суточного
графика
Ветер Время
суток, ч.
0-4 4-8 8-12
12-16 16-20 20-24
Легкий 0,250 0,128
0,086 0,086 0,086 0,128
Слабый 0,318 0,308
0,194 0,222 0,163 0,308
Умеренный 0,500 0,461
0,334 0,382 0,267 0,461
Свежий 0,931 0,562
0,485 0,485 0,485 0,562
Сильный 1 0,981 0,584
0,668 0,542 0,981
Крепкий 1 1 0,935 1
0,750 1
Очень крепкий 1 1 1 1
1 1
3. Анализ
режимов, связанных с аккумулированием
энергии
При решении
вопросов, связанных с аккумулированием энергии, производимой
ветроустанов-кой, необходимо также учитывать, что источник энергии
обладает большой изменчивостью и его режимы заранее предсказать с
большой точностью трудно, а задачи разработки соответствующих методов и
эффективных устройств являются одними из важнейших и сложных проблем
ветроэнергетики.
В основе
анализа режимов, связанных с аккумулированием энергии, производимой
ветроустанов-кой, рассматривается построение модели, содержащей
информацию о недоиспользованной вырабатываемой мощности, с учетом
покрытия графика нагрузки.
Модель может
быть представлена такими нечеткими отношениями, как возможность
использования “избыточной” энергии в определенный период и
характеристикой силы ветра. Здесь, X -описывает множество характеристик
силы ветра, взятые по шкале Бофорта, У - множество характеристик
вырабатываемой мощности, Z - множество суточных интервалов нагрузки,
нечеткое отношение Ь - описывает выработку мощности ВЭУ при
определенном ветре, N - покрытие суточного графика нагрузки, а М -
недоиспользованная вырабатываемая мощность, с учетом покрытия графика
нагрузки в заданный период времени.
Для
построения нечеткого отношения М (табл. 8) можно также воспользоваться
понятием условного нечеткого подмножества. Тогда, аналогично алгоритму
нахождения нечеткого отношения N покрытия суточного графика нагрузки
(табл. 4), отношение, задающее нечеткое подмножество определится как
л(<у,к>)=тах(тт(л(у//к), л(у)), где к=(Рвэу—Рнагр)/Рвэу.
Если
значение коэффициента к отрицательно, значит электрическая нагрузка
покрывается не полностью и возможности аккумулирования нет. В этом
случае коэффициенту присваивается нулевое значение.
Результат
операции тахтт-ой композиции отношений табл. 5 и 7 может быть
представлен в виде нечеткого отношения (табл. 9). При построении данной
модели необходимо учесть тот фактор, что при недостаточной для покрытия
нагрузки скорости ветра, аккумулирование энергии не происходит. В
предыдущем отношении этот фактор учитывается коэффициентом к
, а в данном случае требуется обратиться к значениям принадлежности
покрытия нагрузки (табл. 6).
Если
ль®л(<ад>) < 1, то Ль®л(<Х,г,>) = 0.
Если ЛияЛ^г?) = 1, то
ль®л(<ад>) * 0, т.е. ве-троустановка вырабатывает резервную
мощность.
Где ® - композиция
нечетких отношений, при помощи тахтт-ой процедуры.
Недоиспользованная мощность установки, отн. ед.
Уровень
использования мощности Время суток, ч
0-4
4-8 8-12 12-16 16-20 20-24
Очень малый 0 0 0 0 0
0
Малый 0 0 0 0 0 0
Средний 0 0 0 0 0 0
Больше среднего 0,250
0 0 0 0 0
Большой 0,570 0,270 0
0 0 0,270
Очень большой 0,750
0,570 0,200 0,290 0 0,540
Максимальный 0,800
0,600 0,200 0,300 0 0,600
Недоиспользованная
вырабатываемая мощность, с учетом покрытия графика нагрузки, отн. ед.
Уровень
использования мощности Время суток, ч
0-4
4-8 8-12 12-16 16-20 20-24
Очень малый 0 0 0 0 0
0
Малый 0 0 0 0 0 0
Средний 0 0 0 0 0 0
Больше среднего 0 0 0
0 0 0
Большой 0,57 0 0 0 0 0
Очень большой 0,75
0,53 0 0,29 0 0,53
Максимальный 0,80 0,60
0,20 0,30 0 0,60
Заключение
Показано,
что лингвистическая переменная ветра может быть представлена
упорядоченным терм множеством нечетких переменных. Данный подход
позволяет предсказать возможную выработку электрической энергии с
помощью ВЭУ.
Используя
методику построения нечетких отношений, представлена возможность
сопоставления вырабатываемой мощности с графиком нагрузки, на основании
чего можно сделать вывод об использовании или аккумулировании
электрической энергии.
Простота,
наглядность и прозрачность данного подхода также создает предпосылку
для нечеткого управления, что требует дополнительных исследований.
СПИСОК ЛИТЕРАТУРЫ
1. Шефтер
Я.И. Использование энергии ветра. - М.: Энергоато-миздат, 1983. - 200
с.
2. Ресурсы и
эффективность использования возобновляемых источников энергии в России
/ Под ред. П.П. Безруких. - СПб.: Наука, 2002. - 314 с.
3. Заде Л.
Понятие лингвистической переменной и его применение к принятию
приближённых решений / Пер. с англ.
Н.И. Ринго.
Под ред. Н.Н. Моисеева и С.А. Орловского. - М.: Мир, 1976. - 165 с.
4. Нечеткие
множества и теория возможностей. Последние достижения / Под ред. Р.Р.
Ягера. - М.: Радио и связь, 1986. - 408 с.
5. Кофман А.
Введение в теорию нечетких множеств - М.: Радио и связь, 1982. - 432 с.