Алгоритм Дейкстры

Введение

Алгоритм Дейкстры называют кротчайшим путем единственного источника. Он также известен как единственная исходная проблема кратчайшего пути. Алгоритм вычисляет длину кратчайшего пути от источника к каждому из оставшихся вершин графа.
Проблема единственного источника кратчайшего пути может быть описана следующим образом:
Пусть G = {V, E} ориентированный взвешенный граф, имеющий множество вершин. Особая вершина s в V, где s является источником для любого ребра е из Е, EdgeCost (е) длину ребра е. Все веса в графе должно быть неотрицательным.
Прежде чем подробно рассказывать об алгоритме Дейкстры поговорим подробно о направленно-взвешенном графе.
Направленный граф может быть определена как упорядоченная пара G = (V, E) с V представляет собой набор, элементы которого называются вершинами или узлами, и Е, которое представляет собой множество упорядоченных пар вершин, называемых ориентированными ребрами, дуги, или стрелки. Ориентированные графы также известны как диграфы.

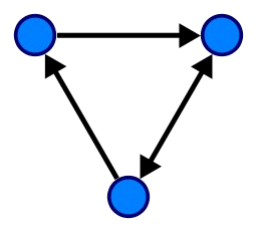
Рисунок 1 - Направленный граф

Направленно-взвешенный граф представляет собой ориентированный граф с весом каждого ребра, который прикреплен к каждому краю графика.

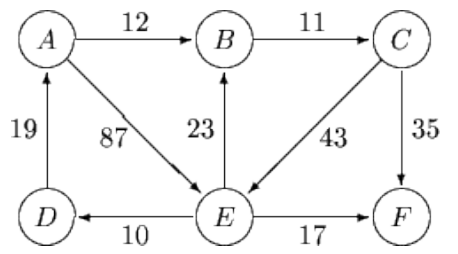
Рисунок 2 - Направленно-взвешенный граф

Жадные алгоритмы используют проблемные методы решения, основанные на действиях, чтобы видеть есть ли лучшая долгосрочная стратегия. Алгоритм Дейкстры использует жадный подход, чтобы решить единственный источник самой короткой проблемы. Это неоднократно выбирает из невыбранных вершин, вершину v, которая ближе всего к источнику s и объявляет, что это расстояние - фактически самое короткое расстояние от s до v. Края v проверяются для того, чтобы видеть, достигнуто ли их назначение исходящих ребер.

Описание алгоритма

Прежде чем углубляться в детали псевдокода алгоритма важно знаеть, как работает алгоритм. Алгоритм Дейкстры работает путем решения подзадачи К, который вычисляет кратчайший путь от источника к вершинам среди К-ближайших вершины к источнику. Для работы алгоритма Дейкстры это должен быть направленно-​​взвешенный граф и края не должны быть отрицательными. если края отрицательны, то фактически кратчайший путь не может быть получен.

В К-том контуре будет набор под названием Граница k вершин, которые будут состоять из вершин, самых близких к источнику и вершин, которые лежат вне границы. Они вычислены и помещены в новую границу. Полученное самое короткое расстояние сохраняется в sDist[w]. Это содержит оценку расстояния от s до w. Алгоритм Дэйкстры находит следующую самую близкую вершину, сохраняя новые граничные вершины в приоритетной очереди .

Алгоритм работает, сохраняя кратчайшее расстояние от вершины V к источнику в массиве sDist. Самое короткое расстояние от источника до него самого равна нулю. sDist для всех других вершин устанавливается в бесконечность, чтобы указать, что эти вершины еще не обработанные. После того, как алгоритм заканчивает обработку вершин, в sDist будет кратчайшее расстояние от вершины W до S. Два комплекта поддерживают пограничный и новые рубежи, которые помогают в обработке алгоритма. Границы относятся к вершинам, которые стоят ближе к источнику. Они будут иметь уже кратчайшие расстояния до этих вершин, ограниченных до K вершин. Вершины, которые находятся за пределами границ помещается в наборе под названием новая граница

Псевдокод алгоритма

Следующий псевдокод описывает работу алгоритма.

Алгоритм иллюстрирует Best-First-Breadth-First поиск. Это Best-First, потому что лучшая вершина выбирается для того, чтобы быть затем обработанной. Используемый Breadth-First поиск, начиная с новой границы, состоит из вершин, которые могут быть испробованы и исследованы от края до края.