Автор: Супонин О.

Разработка моделей параллельной системы прогнозирования поведения движущегося объекта

Введение

Сегодня весьма актуальной является тема программирования поведения движущихся объектов. Технический прогресс сделал большой шаг вперед и сегодня создается огромное множество проектов от нейронных нитей и заканчивая огромными космическими кораблями, морскими судами, авиалайнерами и другими движущимися объектами.

Актуальность моделей движущегося объекта заключается в том, что необходимо заранее знать и уметь рассчитывать и просчитывать поведение объекта в зависимости от внешних факторов и установок пользователя.

Существуют различные алгоритмы пути и траектории маршрута, способы их расчета и реализации на параллельных и последовательных вычислителях одно и многопроцессорных систем.

В данной работе рассматриваются генерация алгоритмов траектории Флойда-Уоршелла, Дейкстры и алгоритм Беллмана-Форда. В качестве фильтра рассматривается фильтр Калмана. Так же рассматриваются параллельные архитектуры, основанные на параллельных многопроцессорных и графических многопроцессорных системах.

1 Алгоритмы генерации траекторий
1.1 Алгоритм Флойда – Уоршелла

Алгоритм Флойда — Уоршелла — алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без иклов с отрицательными весами с использованием метода динамического программирования. Является базовым алгоритмом генерации траектории. В основе алгоритма лежат два свойства кратчайшего пути графа. Первое:
Имеется кратчайший путь p_1k=(v₁,v₂,… ,v_k) от вершины v₁ до вершины v_k, а также его подпуть p'(v_i,v_i+1,… ,v_j), при этом действует 1 <= i <= j <= k.
Если p — кратчайший путь от v₁ до v_k, то p' также является кратчайшим путем от вершины v_i до v_j

Это можно легко доказать, так как стоимость пути p складывается из стоимости пути p' и стоимости остальных его частей. Представив, что есть более короткий путь p', уменьшается сумма, что приводит к противоречию с утверждением, что эта сумма и так уже была минимальной.
Второе свойство является основой алгоритма. Рассматривается граф G с пронумерованными от 1 до n вершинами {v₁,v₂,… ,v_n} и путь p_ij от v_i до v_j, проходящий через определенное множество разрешенных вершин, ограниченное индексом k.

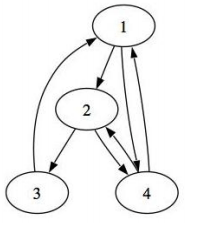
Рисунок 1.1.1 - Граф

То есть если k=0, то рассматриваются прямые соединения вершин друг с другом, так как множество разрешенных промежуточных вершин рано нулю. Если k=1 — рассматриваются пути, проходящие через вершину v₁, при k=2 — через вершины {v₁, v₂}, при k=3 — {v₁, v₃, v₃} и так далее. Рассмотрим граф на Рисунке 1.1.1 k=1, то есть в качестве промежуточных узлов разрешен только узел «1». В этом графе при k=1 нет пути p₄₃, но есть при k=2, тогда можно добраться из «4» в «3» через «2» или через «1» и «2».

Рассмотрим кратчайший путь p_ij с разрешенными промежуточными вершинами {1..k-1} стоимостью d_ij. Теперь расширим множество на k- тый элемент, так что множество разрешенных вершин станет {1..k}. При таком расширении возможно 2 исхода:
Случай 1. Элемент k не входит в кратчайший путь p_ij, то есть от добавления дополнительной вершины мы ничего не выиграли и ничего не изменили, а значит стоимость кратчайшего пути d^k_ij не изменился, соответственно
d^k_ij = d^k-1_ij — просто перенимаем значение до увеличения k.
Случай 2. Элемент k входит в кратчайший путь p_ij, то есть после добавления новой вершины в можество разрешенных, кратчайший путь изменился и проходит теперь через вершину v_k.

Новый кратчайший путь разбит вершиной v_k на p_ik и p_kj, используем первое свойство, согласно ему, p_ik и p_kj также кратчайшие пути от v_i до v_kи от v_k до v_j соответственно. Значит d^k_ij = d^k_ik + d^k_kj , а так как в этих путях k либо конечный, либо начальный узел, то он не входит в множество промежуточных, соответственно его из него можно удалить: d^k_ij = d^k-1_ij + d^k-1_kj.
Посмотрим на значение d^k_ij в обоих случаях — верно! Оно в обоих случаях складывается из значений d для k-1, а значит имея начальные (k=0) значения для d, мы сможем расчитать d для всех последующих значений k. А значения d для k=0 мы знаем, это вес/стоимость рёбер графа, то есть соединений без промужуточных узлов.
При k=n (n — количество вершин) мы получим оптимальные значения d для всех пар вершин.

При увеличении с k-1 до k, какое значение мы сохраним для d^k_ik? Минимумом значений случая 1 и 2, то есть смотрим дешевле ли старый путь или путь с добавлением дополнительной вершины.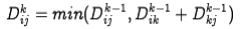

Как видно, сначала происходит инициализация матрицы кратчайших расстояний D⁰, изначально она совпадает с матрицей смежности, в цикле увеличиваем значение k и пересчитываем матрицу расстояний, из D⁰ получаем D¹, из D¹ — D² и так далее до k=n.

Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно. Правда, если не принять специальных мер, то при наличии в графе рёбер отрицательного веса, в результирующей матрице могут появиться числа вида ∞-1, ∞-2, и т.д., которые, конечно, по-прежнему означают, что между соответствующими вершинами вообще нет пути. Поэтому при наличии в графе отрицательных рёбер алгоритм Флойда лучше написать так, чтобы он не выполнял переходы из тех состояний, в которых уже стоит «нет пути»

2.2 Алгоритм Дейкcтры
Данный алгоритм находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса и широко применяется в программировании.
Суть алгоритма заключается в следующем.
Имеется ориентированный граф G, который изображен на рисунке 2.2

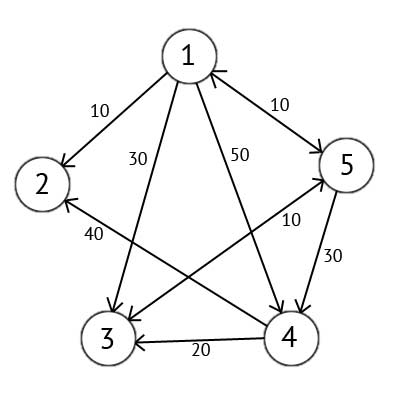
Рисунок 2.2 – Ориентированный граф G
Этот граф мы можем представить в виде матрицы С:
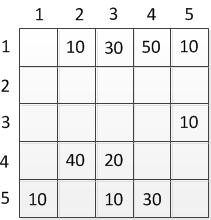
Таблица 2.2 - Матрица ориентированного графа

Выбираем вершину 1. Это означает, что будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5. Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере. Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.

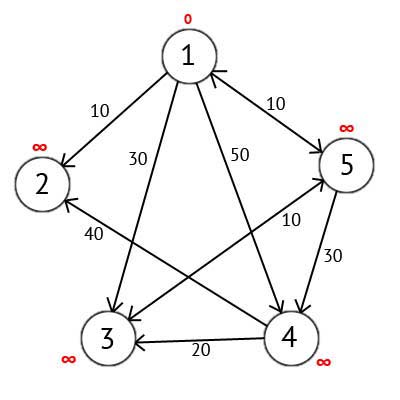
Рисунок 2.3 – Ориентированный граф после первого шага

Далее выберем такую вершину W, которая имеет минимальную метку и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.

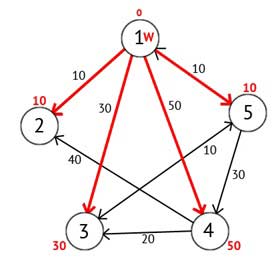
Рисунок 2.4 – Ориентированный граф после второго шага

Далее вершину W отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них можно выбрать как W.

Выберем вершину 2. Из нее нет ни одного исходящего пути, значит можно сразу отметить вершину как посещенную и перейти к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму.

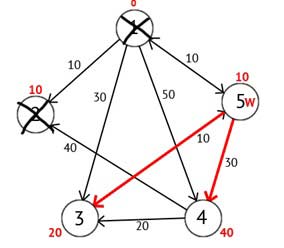
Рисунок 2.5 – Ориентированный граф после третьего шага

Исходя из рисунка 2.5 можно увидеть, что метки 3-ей и 4-ой вершин стали меньше, то есть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть не посещённые вершины.
Выполнив все действия, получим такой результат:

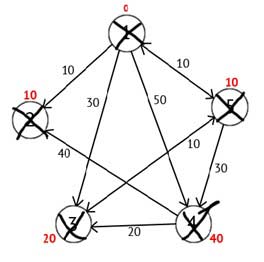
Рисунок 2.6 – Ориентированный граф на конечном шаге

3 Фильтр Калмана

Для улучшения качества сигнала необходимо проводить фильтрацию. Фильтрация — это алгоритм обработки данных, который убирает шумы и информацию, которая искажает полезность сигнала. Одним из распространенных фильтров является фильтр Калмана.

Фильтр Калмана — это алгоритм фильтрации, используемый во многих областях науки и техники. Его можно встретить в GPS-приемниках, интеллектуальных датчиках, в различных системах управления. Он использует динамическую модель системы. Алгоритм состоит из двух повторяющихся фаз: предсказание и корректировка. На первом рассчитывается предсказание состояния в следующий момент времени (с учетом неточности их измерения). На втором, новая информация с датчика корректирует предсказанное значение (также с учетом неточности и зашумленности этой информации):

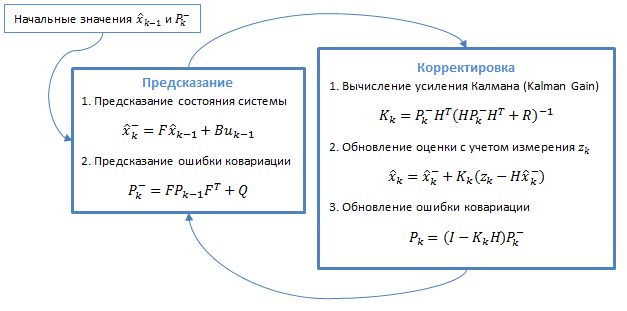
Рисунок 3.1 – Общий алгоритм фильтра

3.1 Модель динамической системы

Фильтры Калмана базируются на дискретизированных по времени линейных динамических системах. Состояние системы описывается вектором конечной размерности — вектором состояния. В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния (детерминированное изменение состояния), добавляется некоторый вектор нормального шума (случайные факторы) и в общем случае вектор управления, моделирующий воздействие системы управления.

При использовании фильтра Калмана для получения оценок вектора состояния процесса по серии зашумленных измерений необходимо представить модель данного процесса в соответствии со структурой фильтра — в виде матричного уравнения определенного типа. Для каждого такта k работы фильтра необходимо в соответствии с приведенным ниже описанием определить матрицы: перехода между состояниями F_k; матрицу измерений H_k; ковариационную матрицу шума процесса Q_k; ковариационную матрицу шума измерений R_k; при наличии управляющих воздействий — матрицу коэффициентов B_k.

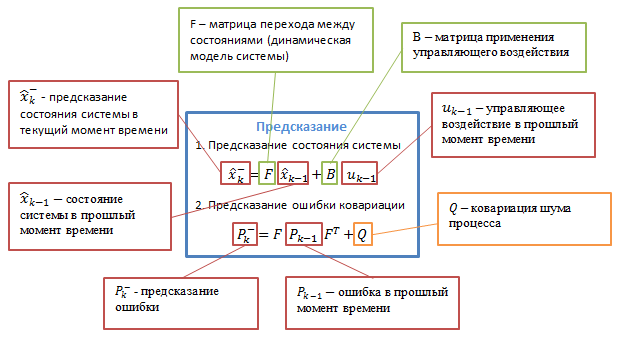
Рисунок 3.2 – Подробное описание алгоритма x_k = F_kx_k-1 + B_ku_k + w_k, где F_k — матрица эволюции процесса/системы, которая воздействует на вектор x_k−1 (вектор состояния в момент k−1);
B_k — матрица управления, которая прикладывается к вектору управляющих воздействий u_k;
w_k — нормальный случайный процесс с нулевым математическим ожиданием и ковариационной матрицей Q_k, который описывает случайный характер эволюции системы/процесса: w_k ~ N(0,Q).
В момент k производится наблюдение (измерение) z_k истинного вектора состояния x_k, которые связаны между собой уравнением: z_k = H_kx_k + v_k, где
H_k — матрица измерений, связывающая истинный вектор состояния и вектор произведенных измерений, v_k — белый гауссовский шум измерений с нулевым математическим ожиданием и ковариационной матрицей R_k: v_k ~ N(0,R_k)

Фильтр Калмана является разновидностью рекурсивных фильтров. Для вычисления оценки состояния системы на текущий такт работы ему необходима оценка состояния (в виде оценки состояния системы и оценки погрешности определения этого состояния) на предыдущем такте работы и измерения на текущем такте. Данное свойство отличает его от пакетных фильтров, требующих в текущий такт работы знание истории измерений и/или оценок. Далее под записью X́_n|m будем понимать оценку истинного вектора x в момент n с учетом измерений с момента начала работы и по момент m включительно.

Ṕ_k|k — апостериорная ковариационная матрица ошибок, задающая оценку точности полученной оценки вектора состояния и включающая в себя оценку дисперсий погрешности вычисленного состояния и ковариации, показывающие выявленные взаимосвязи между параметрами состояния системы (в русскоязычной литературе часто обозначается D́_k);
X́_k|k — апостериорная оценка состояния объекта в момент k полученная по результатам наблюдений вплоть до момента k включительно (в русскоязычной литературе часто обозначается X́_k, где X́ означает «оценка», а k – номер такта, на котором она получена).

В качестве движущегося объекта выберем судно, движение которого описывается системой дифференциальных уравнений: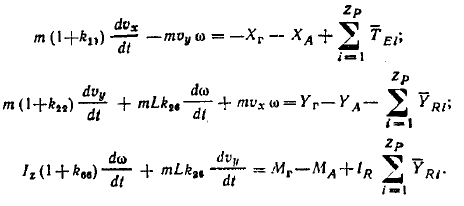

где: , (рис 3.3).

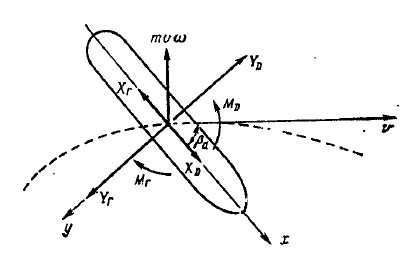
Рисунок 3.3 - Параметры модели судна.

3 Параллельные архитектуры

В компьютерных науках параллелизм — это свойство систем, при которой несколько вычислений выполняются одновременно, и при этом, возможно, взаимодействуют друг с другом. Вычисления могут выполняться на нескольких ядрах одного чипа с вытесняющим разделением времени потоков вычислений на одном процессоре, либо выполняться на физически отдельных процессорах.

3.1 Параллелизм как основа высокопроизводительных вычислений

Без каких-либо особенных преувеличений можно заявить, что все развитие компьютерных систем происходило и происходит под девизом «Скорость и быстрота вычислений». Если быстродействие первой вычислительной машины ENIAC составляло всего несколько тысяч операций в секунду, то самый быстрый на данный момент времени суперкомпьютер RoadRunner может выполнять уже квадриллионы (1015) команд. Темп развития вычислительной техники просто впечатляет – увеличение скорости вычислений в триллионы (1012) раз не многим более чем за 60 лет. История развития вычислительной техники представляет увлекательное описание замечательных научно-технических решений, радости побед и горечи поражений.

Проблема создания высокопроизводительных вычислительных систем относится к числу наиболее сложных научно-технических задач 17 современности и ее разрешение возможно только при всемерной концентрации усилий многих талантливых ученых и конструкторов, предполагает использование всех последних достижений науки и техники и требует значительных финансовых инвестиций. Важно отметить при этом, что при общем росте скорости вычислений в 1012 раз, быстродействие самих технических средств вычислений увеличилось всего в несколько миллионов раз. И дополнительный эффект достигнут за счет введения параллелизма буквально на всех стадиях и этапах вычислений.

Рисунок 3.1 – Параллельная структура

3.1.1 Симметрическая мультипроцессорность
Организация симметричной мультипроцессорности (Symmetric Multiprocessor, SMP), когда в рамках одного вычислительного устройства имеется несколько полностью равноправных процессоров, является практически первым использованным подходом для обеспечения многопроцессорности – первые вычислительные системы такого типа стали появляться в середине 50-х – начале 60-х годов, однако массовое применение SMP систем началось только в середине 90-х годов. Следует отметить, что SMP системы входят в группу MIMD (multi instruction multi data) вычислительных систем в соответствии с классификацией Флинна. Поскольку эта классификация приводит к тому, что практически все виды параллельных систем (несмотря на их существенную разнородность) относятся к одной группе MIMD, для дальнейшей детализации класса MIMD предложена практически общепризнанная структурная. В рамках данной схемы дальнейшее разделение типов многопроцессорных систем основывается на используемых способах организации оперативной памяти в этих системах. Данный поход позволяет различать два важных типа многопроцессорных систем – multiprocessors (мультипроцессоры или системы с общей разделяемой памятью) и 18 multicomputers (мультикомпьютеры или системы с распределенной памятью).

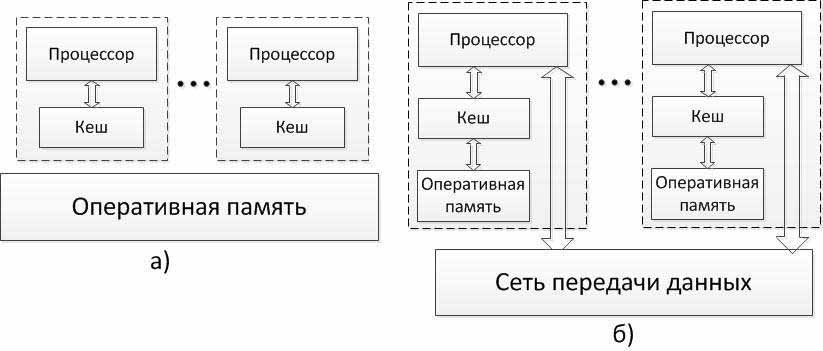
Рисунок 3.2 – Архитектура многопроцессорных систем с общей (разделяемой) памятью: системы с (а) однородным и (б) неоднородным доступом к памяти

Для дальнейшей систематики мультипроцессоров учитывается способ построения общей памяти. Возможный подход – использование единой (централизованной) общей памяти (shared memory) – см. рис. 1.2. Такой подход обеспечивает однородный доступ к памяти (uniform memory access or UMA) и служит основой для построения векторных параллельных процессоров (parallel vector processor or PVP) и симметричных мультипроцессоров (symmetric multiprocessor or SMP). Среди примеров первой группы суперкомпьютер Cray T90, ко второй группе относятся IBM eServer, Sun StarFire, HP Superdome, SGI Origin и др.

Одной из основных проблем, которые возникают при организации параллельных вычислений на такого типа системах, является доступ с разных процессоров к общим данным и обеспечение, в этой связи, однозначности (когерентности) содержимого разных кэшей (cache coherence problem). Дело в том, что при наличии общих данных копии значений одних и тех же переменных могут оказаться в кэшах разных процессоров.

Если в такой ситуации (при наличии копий общих данных) один из процессоров выполнит изменение значения разделяемой переменной, то значения копий в кэшах других процессорах окажутся не соответствующими действительности и их использование приведет к некорректности вычислений. Обеспечение однозначности кэшей обычно реализуется на аппаратном уровне – для этого после изменения значения общей переменной все копии этой переменной в кэшах отмечаются как недействительные и последующий доступ к переменной потребует обязательного обращения к основной памяти. Следует отметить, что необходимость обеспечения 19 когерентности приводит к некоторому снижению скорости вычислений и затрудняет создание систем с достаточно большим количеством процессоров.

Наличие общих данных при выполнении параллельных вычислений приводит к необходимости синхронизации взаимодействия одновременно выполняемых потоков команд. Так, например, если изменение общих данных требует для своего выполнения некоторой последовательности действий, то необходимо обеспечить взаимоисключение (mutual exclusion) с тем, чтобы эти изменения в любой момент времени мог выполнять только один командный поток. Задачи взаимоисключения и синхронизации относятся к числу классических проблем, и их рассмотрение при разработке параллельных программ является одним из основных вопросов параллельного программирования.

Общий доступ к данным может быть обеспечен и при физически распределенной памяти (при этом, естественно, длительность доступа уже не будет одинаковой для всехэлементов памяти) – см. рис. 1.2. Такой подход именуется как неоднородный доступ к памяти (non-uniform memory access or NUMA). Среди систем с таким типом памяти выделяют:

Системы, в которых для представления данных используется только локальная кэш-память имеющихся процессоров (cache-only memory architecture or COMA); примерами таких систем являются, например, KSR-1 и DDM;

Системы, в которых обеспечивается когерентность локальных кэшей разных процессоров (cache-coherent NUMA or CC-NUMA); среди систем данного типа SGI Origin 2000, Sun HPC 10000, IBM/Sequent NUMA-Q 2000;

Системы, в которых обеспечивается общий доступ к локальной памяти разных процессоров без поддержки на аппаратном уровне когерентности кэша (non-cache coherent NUMA or NCC-NUMA); к данному типу относится, например, система CrayT3E.

Использование распределенной общей памяти (distributed shared memory or DSM) упрощает проблемы создания мультипроцессоров (известны примеры систем с несколькими тысячами процессоров), однако, возникающие при этом проблемы эффективного использования распределенной памяти (время доступа к локальной и удаленной памяти может различаться на несколько порядков) приводят к существенному повышению сложности параллельного программирования.

3.2 Параллельная архитектура GPU

Графический процессор (англ. graphics processing unit, GPU) — отдельное устройство персонального компьютера, выполняющее графический рендеринг. Современные графические процессоры очень эффективно обрабатывают и отображают компьютерную графику. Благодаря специализированной конвейерной архитектуре они намного эффективнее в обработке графической информации, чем типичный центральный процессор.

Вычисления на GPU заключаются в использовании графического процессора совместно с CPU для ускорения универсальных приложений в области науки и проектирования. Вычисления на GPU были изобретены компанией NVIDIA и быстро стали стандартом в индустрии, который используют миллионы пользователей по всему миру и который приняли практически все производители компьютерных систем.

Вычисления на GPU предлагают беспрецедентную производительность приложений благодаря тому, что GPU обрабатывает части приложения, требующие большой вычислительной мощности, при этом остальная часть приложения выполняется на CPU. С точки зрения пользователя, приложение просто работает значительно быстрее.

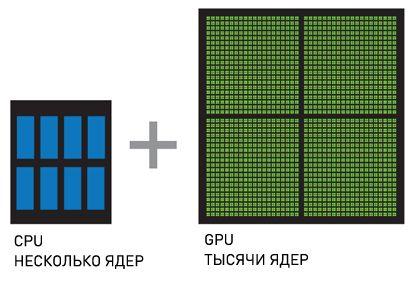
CPU + GPU – это мощная комбинация, потому что CPU состоят из нескольких ядер, оптимизированных для последовательной обработки данных, в то время как GPU состоят из тысячи маленьких, более производительных ядер, созданных для параллельной обработки данных. Последовательные части кода обрабатываются на CPU, а параллельные части - на GPU.

4 Параллельные реализации
4.1.1 Реализация интерфейса MPI

Message Passing Interface (MPI, интерфейс передачи сообщений) — программный интерфейс для передачи информации, который позволяет обмениваться сообщениями между процессами, выполняющими одну задачу.

MPI является наиболее распространённым стандартом интерфейса обмена данными в параллельном программировании, существуют его реализации для большого числа компьютерных платформ. Используется при разработке программ для кластеров и суперкомпьютеров. Основным средством коммуникации между процессами в MPI является передача сообщений друг другу. Стандартизацией MPI занимается MPI Forum. В стандарте MPI описан интерфейс передачи сообщений, который должен поддерживаться как на платформе, так и в приложениях пользователя.

В первую очередь MPI ориентирован на системы с распределенной памятью, то есть когда затраты на передачу данных велики, в то время как OpenMP ориентирован на системы с общей памятью (многоядерные с общим кэшем). Обе технологии могут использоваться совместно, дабы оптимально использовать в кластере многоядерные системы.

4.1.2 Функционирование интерфейса

Базовым механизмом связи между MPI процессами является передача и приём сообщений. Сообщение несёт в себе передаваемые данные и информацию, позволяющую принимающей стороне осуществлять их выборочный приём:

отправитель — ранг (номер в группе) отправителя сообщения;

получатель — ранг получателя;

признак — может использоваться для разделения различных видов сообщений;

коммуникатор — код группы процессов.

Операции приёма и передачи могут быть блокирующимися и не блокирующимися. Для не блокирующихся операций определены функции проверки готовности и ожидания выполнения операции. Другим способом связи является удалённый доступ к памяти (RMA), позволяющий читать и изменять область памяти удалённого процесса. Локальный процесс может переносить область памяти удалённого процесса (внутри указанного процессами окна) в свою 22 память и обратно, а также комбинировать данные, передаваемые в удалённый процесс с имеющимися в его памяти данными (например, путём суммирования). Все операции удалённого доступа к памяти не блокирующиеся, однако, до и после их выполнения необходимо вызывать блокирующиеся функции синхронизации.

4.2 CUDA

CUDA ( Compute Unified Device Architecture) — программно-аппаратная архитектура параллельных вычислений, которая позволяет существенно увеличить вычислительную производительность благодаря использованию графических процессоров фирмы NVIDIA.

В архитектуре CUDA используется модель памяти грид, кластерное моделирование потоков и SIMD-инструкции. Применима не только для высокопроизводительных графических вычислений, но и для различных научных вычислений с использованием видеокарт nVidia. Ученые и исследователи широко используют CUDA в различных областях, включая астрофизику,вычислительную биологию и химию, моделирование динамики жидкостей, электромагнитных взаимодействий, компьютерную томографию, сейсмический анализ и многое другое. В CUDA имеется возможность подключения к приложениям, использующим OpenGL и Direct3D. CUDA - кроссплатформенное программное обеспечение для таких операционных систем как Linux, Mac OS X и Windows.

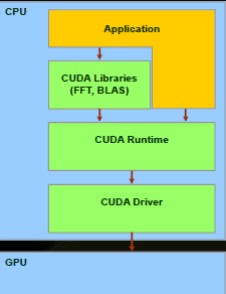
Рисунок 4.2.1 Общая структура устройства Cuda

CUDA дает разработчику возможность по своему усмотрению организовывать доступ к набору инструкций графического ускорителя и управлять его памятью, организовывать на нем сложные параллельные вычисления. Графический ускоритель с поддержкой CUDA становится мощной программируемой открытой архитектурой, подобно сегодняшним центральным процессорам. Всё это предоставляет в распоряжение разработчика низкоуровневый, распределяемый и высокоскоростной доступ 24 к оборудованию, делая CUDA необходимой основой при построении серьезных высокоуровневых инструментов, таких как компиляторы, отладчики, математические библиотеки, программные платформы.

4.2.1 Возможности технологии CUDA

– стандартный язык C для параллельной разработки приложений на GPU;
– стандартные библиотеки численного анализа для быстрого преобразования Фурье и базового пакета программ линейной алгебры;
– специальный драйвер CUDA для вычислений с быстрой передачей данных между GPU и CPU;
– драйвер CUDA взаимодействует с графическими драйверами OpenGL и DirectX;
– поддержка операционных систем Linux 32/64-bit, Windows XP 32/64- bit и Mac.

ВЫВОД

Затронув основные аспекты генерации траектории движущихся объектам в рамках выбранной темы в данной работе были рассмотрены основные алгоритмы генерации траектории, а именно алгоритм Дейкстры, алгоритм Беллмана-Форда и алгоритм Флойда-Уоршелла. Были приведены примеры, по которым можно понять принципы работы алгоритмов. Практически любую систему невозможно представить без всевозможных фильтров. В данной сфере широко применяется фильтр Калмана. Он позволяет сгладить результаты и выявить более точные вычисления для требуемых задач.
Реализация вычисления используется на многопроцессорных системах. В данной работе были представлены основы многопроцессорной параллельной системы и основы GPU, которые реализованы на технологии компании Nvidia – CUDA. Все больше и больше людей используют данную технологию в научных целях, когда необходимо выполнить расчеты с большим количеством численных данных.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. www.Wikipedia.com
2. www.habrahabr.ru
3. www.nvidia.com
4. Гергель В.П. – Высокопроизводительные вычисления для многоядерных компьютерных систем 2010.