Визильтер Ю.В, Вишняков Б.В. (ФГУП ГосНИИ Авиационных Систем)

Исследование поведения авторегрессионных фильтров
в задаче выделения и анализа движения на цифровых видеопоследовательностях¹


В статье описаны авторегрессионная фильтрация измерений с оптимальным выбором параметра сглаживания и повторная сглаживающая авторегрессионная фильтрация для оценки параметров видимого движения и размеров объектов на изображениях. Предложен способ исследования пиксельного временного сигнала на базе вычисления кратнорегрессионных псевдоспектров для анализа оптических потоков.


Keywords: Motion analysis; Object detection; Autoregression filtering.

Введение

В статьях [1, 2] были рассмотрены основные задачи, связанные с автоматическим выделением и сопровождением объектов по признаку их движения на изображениях, получаемых от различных видеодатчиков.

В статье [1] предложена оригинальная методика выделения и межкадрового прослеживания движущихся объектов на подвижном фоне. Тестирование разработанных алгоритмов на большом объеме реальных видеоданных показало высокую эффективность использования предложенного подхода для выделения мелкоразмерных движущихся объектов, площадь которых существенно меньше площади анализируемого кадра.

Однако в большинстве систем видеонаблюдения типичной является ситуация, когда размер движущегося объекта заранее не известен, и, следовательно, система детектирования движения должна обеспечивать возможность адаптивной настройки алгоритмов на крупно-, средне- и мелкоразмерные объекты, в зависимости от задачи наблюдения, поля зрения и текущих настроек объектива камеры.

Для решения этой проблемы в статье [2] предложен так называемый «модифицированный метод оптических потоков», который является обобщением разностного подхода, предложенного в работе [3]. В рамках данного метода на этапе предобработки используются временные разностно-накопительные схемы, оптический поток вычисляется по разности накопленных изображений, движущиеся элементы изображения определяются на основе оценки накопленного оптического потока. При этом также обеспечивается статистическое межкадровое прослеживание движущихся объектов как устойчивых во времени связных групп сходно движущихся элементов изображения.

Разработанные алгоритмы обеспечивают помехоустойчивость и вычислительную эффективность на уровне ранее предложенного алгоритма для выделения мелкоразмерных движущихся объектов и, в то же время, дают возможность настройки алгоритма на выделение не только мелкоразмерных, но также средне- и крупноразмерных объектов (занимающих до 30-40% площади кадра).

Однако при практической реализации методов межкадрового прослеживания объектов, помимо задач собственно анализа последовательности цифровых изображений, рассматривавшихся в предыдущих публикациях, не меньшее значение приобретают такие задачи как оценка предельно допустимого значения контрастности движущегося объекта, при котором он может быть обнаружен на некотором фоне, а также задача статистического оценивания параметров движения объекта и его размеров.

Данная статья посвящена решению этих задач при помощи хорошо изученного аппарата авторегрессионных временных фильтров. Исследование поведения и свойств этих фильтров применительно к задаче оценивания движения на цифровых изображениях позволяет обосновать ряд новых алгоритмических решений. Также в качестве обобщения введенного ранее метода сравнения накопленных яркостей вводится понятие «кратнорегрессионных псевдоспектров».

Оценивание параметров движения и размеров видимых объектов

Поскольку фильтрация измерений в данном исследовании рассматривается применительно к измерениям размеров, координат и скоростей движущихся объектов, получаемых на основе модифицированного метода анализа оптических потоков, то применяемая процедура должна обладать следующими свойствами:

1. 
   Минимальное «биение» оценок размеров и координат движущегося объекта, т. е. график, описывающий поведение оцениваемой величины, должен быть «достаточно гладким». Данное свойство наиболее важно для оценки размеров объекта, так как они часто могут измеряться ошибочно, например, при пересечении с другими объектами, частичном или полном перекрытии (заслонении) неподвижными объектами сцены наблюдения (дома, деревья, мосты и т.п.);
   
2. 
   Минимальное запаздывание оценки измерений и координат, т. е. фильтр должен «успевать» за резким изменением характера поступающих измерений, например, если объект удаляется, и его ширина и высота резко уменьшаются. Заметим, что данное свойство наиболее важно в отношении измерений скорости объекта.
   
3. 
   Робастность: фильтр должен устойчиво обрабатывать измерения с различным поведением ошибки, т. е. распределение вероятностей измерений может существенно отличаться в различных ситуациях. Например, скорость объекта может резко увеличиваться или уменьшаться, а размеры объекта при движении объекта параллельно плоскости кадра в большинстве случаев будут постоянны с точностью до ошибки измерений. В то же время, при развороте объекта его размеры также могут резко меняться одновременно с изменением скорости.
   

Для фильтрации размеров объекта предлагается использовать процедуру авторегрессии первого порядка [4,5]. Фильтрация, основанная на моделях авторегрессии, хороша тем, что является наиболее робастной при работе с объектами, для которых полностью отсутствует априорная информация об оцениваемых параметрах.

Порядок авторегрессии был выбран минимальным – первым – из-за того, что при повышении порядка модели начинает проявляться эффект существенного «запаздывания» оценки. Если измерения скорости объекта начали резко возрастать (например, объект стал разгоняться), то авторегрессионная оценка скорости второго или более высокого порядка будет достаточно продолжительное время сильно отличаться от действительного наблюдаемого значения, что в данном случае неприемлемо с точки зрения практической применимости систем анализа движения.

Найдем методом авторегрессии оценки ширины W, высоты H, вектора скорости V = (V_x,V_y), некоторого объекта на видеопоследовательности на k-м кадре, исходя из оценки, полученной на предыдущем (k-1)-м кадре, и измерения, полученного на k-м кадре.
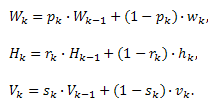(1)

Здесь p_k, r_k, s_k – параметры авторегрессионного фильтра;
W_k, H_k, V_k- случайные величины, имеющие смысл фильтрованных измерений ширины, высоты и скорости соответственно на k-м кадре;
w_k, h_k, v_k – измерения ширины, высоты и скорости на -м кадре.

Таким образом,W_k, H_k, V_k в зависимости от есть случайные процессы авторегрессии первого порядка.

Jчевидно, что результаты, полученные для любого одного из трех выражений (1), могут быть легко обобщены на все три выражения (1) из-за аналогичности структуры. Возьмем первое выражение из (1) и попробуем обосновать некоторую близкую к оптимальности стратегию выбора параметра p_k

Рассмотрим сначала на нескольких характерных примерах, как изменяется поведение авторегрессионного фильтра в зависимости от значения параметра p_k

Пусть p_k ∈ (0,1). Легко заметить, что при выборе параметра p_k достаточно близким к единице влияние нового измерения w_k практически сводится к нулю, а новая оценка W_k практически полностью базируется на старой оценке W_k. Такой выбор параметра делает график последовательности W_k наиболее гладким, но при этом фильтр становится очень инерционным, т. е. при резком изменении характера измерений (например, ширина объекта стала резко меняться) фильтр «не успевает» за измерениями и дает слишком сильную погрешность относительно истинной траектории. На рис. 1. показаны измерения ширины объекта на видеопоследовательности в течение 160 кадров, построены графики W_k для значений параметров:
p_k = 0.7; p_k = 0.9; p_k = 0.99.

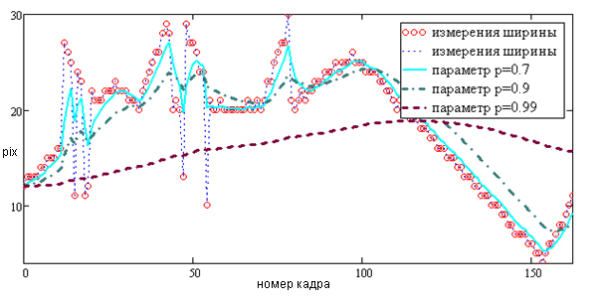
Рис. 1. Поведение авторегрессионной оценки W_k при различном выборе параметра p_k

На рис. 1 измерения ширины отображены кружками и затем для пущей наглядности соединены пунктирной линией. Как видно из данного рисунка, при увеличении параметра p_k кривая W_k становится более гладкой, но перестает «успевать» за уменьшением поступающих измерений ширины w_k.

При p_k = 0.7 кривая практически повторяет измерения. Достоинство выбора данного значения параметра p_k в том, что он легко «успел» за уменьшением ширины объекта. Недостаток же состоит в том, что при данном значении p_k = 0.7 авторегрессионная оценка ширины объекта W_k имеет сильное «биение» в тех точках, где появляется ошибка измерений.

При выборе значения p_k = 0.9 «биение» на ошибках измерений существенно уменьшается, и эффект «запаздывания» практически не заметен.

При p_k = 0.99 значение авторегрессионной оценки W_k очень сильно отличается от измерений и не в силах «успеть» за изменяющейся шириной объекта.

Следовательно. в данном случае наилучшее значение параметра p_k = 0.9.

В то же время в примере фильтрации высоты того же объекта использование значения p_k = 0.99 дает наилучший результат (рис. 2). Это, прежде всего, связано с тем, что на данной последовательности измерения высоты объекта имеют постоянное математическое ожидание. В данном случае «биение», которое вызвано лишь случайной ошибкой, присутствующей в измерении, очень хорошо сглаживается фильтром.

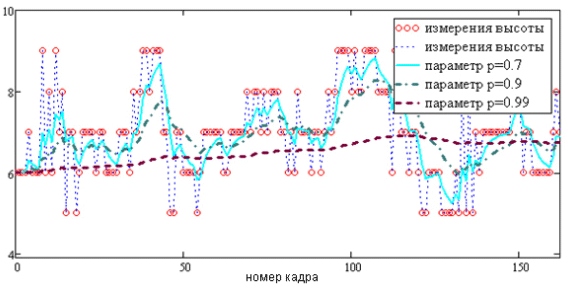
Рис. 2. Поведение авторегрессионной оценки H_k при различном выборе параметра p_k

Определение оптимальной оценки параметра по всей траектории
Необходимо найти оптимальную оценку параметра p_k по всей траектории. Оценка эта традиционно определяется методом наименьших квадратов.

Пусть функционал качества фильтрации имеет вид: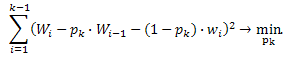
(2)
Минимум квадратичной функции (2) легко найти, приравняв к нулю ее производную. Получим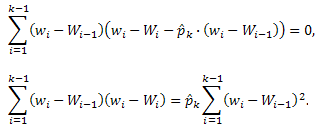

После преобразования окончательно находим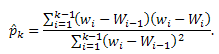
(3)

Начальное значение p₁ можно выбрать любым, например, с учетом результатов предыдущего примера, положить p₁ = 0.9. При этом нужно помнить, что начальное значение p₀ будет сказываться на последующем процессе фильтрации некоторое время с начала работы фильтра. Таким образом, итеративная схема фильтрации будет выглядеть следующим образом: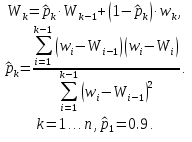
(3)

Результаты выбора оптимального в смысле критерия (3) адаптивного параметра p_k в сравнении с предыдущими результатами для значения параметра p = 0.9 представлены на рис. 3 для авторегрессионной оценки ширины объекта W_k и на рис. 4 для авторегрессионной оценки высоты объекта H_k.

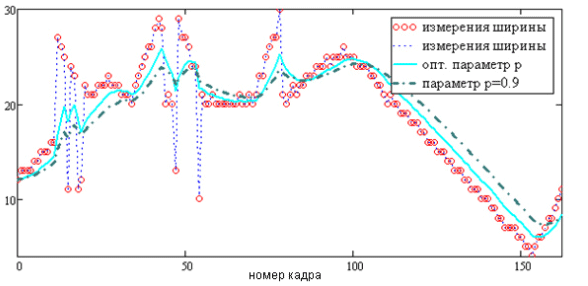
Рис. 3. Поведение авторегрессионной оценки W_k при оптимальном значении параметра p_k и при значении p_k = 0.9

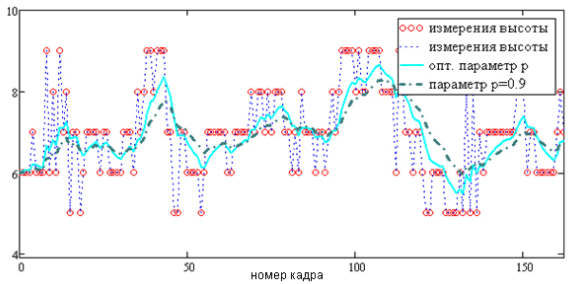
Рис. 4. Поведение авторегрессионной оценки H_k при оптимальном значении параметра p_k и при значении p_k = 0.9

Из рис. 3 и рис. 4 видно, что при оптимальном в смысле критерия (3) выборе параметра фильтр становится более чувствительным, но при этом менее гладким, чем при выборе p_k = 0.9. Такой фильтр удобнее всего использовать для фильтрации третьего параметра объекта – его скорости, где наиболее важным свойством является отсутствие «запаздывания».

Для фильтрации же ширины и высоты, где наиболее важным является свойство «гладкости» кривой, рассмотрим следующий способ.

Повторная сглаживающая авторегрессионная фильтрация

Рассмотрим модель, которая будет фильтровать измерения, полученные с помощью оптимального авторегрессионного фильтра – модель авторегрессии второго уровня, повторно фильтрующая оценки, полученные с помощью оптимального авторегрессионного фильтра первого уровня:

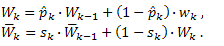(4)

Здесь параметр p_k выбирается в соответствии с формулой (3), а параметр S_k предлагается задавать либо задавать вручную, либо также выбирать оптимальным (S_k) в соответствии с формулой 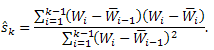(5):

(5)

Смысл данного итеративного процесса таков: первое выражение осуществляет фильтрацию измерений, второе – сглаживание результатов данной фильтрации. Примеры для параметра r_k = 0.9 представлены на рис. 5 и рис. 6.

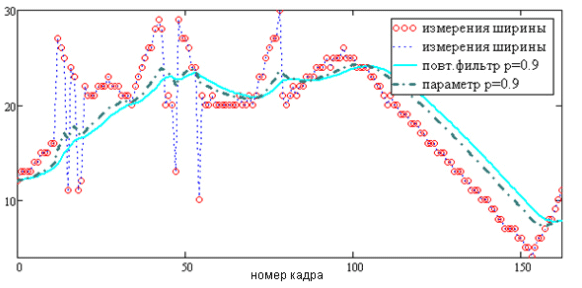
Рис. 5. Поведение повторной авторегрессионной оценки W_k при значении параметра r_k = 0.9 и авторегрессионной оценки при значении p_k = 0.9

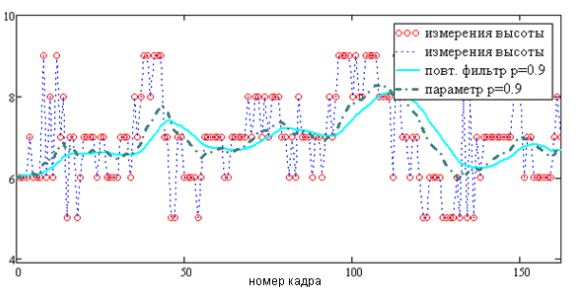
Рис. 6. Поведение повторной авторегрессионной оценки H_k при значении параметра r_k = 0.9 и авторегрессионной оценки при значении p_k = 0.9

Как видно из рис. 5 и 6, кривые авторегрессионных оценок второго уровня H_k и W_k являются наиболее гладкими из всех рассмотренных. Это принципиально важно при фильтрации таких параметров как размеры объектов, поскольку плавность изменения размеров объекта важна не только при обработке поступающей информации о перемещениях объектов, но и при визуализации результатов анализа движения для оператора, осуществляющего наблюдение и принимающего дальнейшие решения.

Заключение

Данное исследование посвящено изучению поведения авторегрессионных фильтров в задаче выделения и анализа движения на цифровых видеопоследовательностях.

В задаче оценки параметров видимого движения и размеров объектов рассмотрены три варианта фильтрации с применением модели авторегрессии первого порядка:

авторегрессионная фильтрация измерений с фиксированным параметром;

авторегрессионная фильтрация измерений с оптимальным выбором параметра;

повторная сглаживающая авторегрессионная фильтрация.

Как показали эксперименты на большом объеме реальных данных видеонаблюдения, наиболее приемлемым способом фильтрации измерений скорости объекта оказался способ авторегрессионной фильтрации с оптимальным выбором параметра, а наиболее приемлемым способом для фильтрации размеров объекта – способ повторной сглаживающей авторегрессионной фильтрации.

Для задачи анализа оптических потоков предложен способ исследования пиксельного временного сигнала на базе вычисления кратнорегрессионных псевдоспектров. Представлена схема кратного авторегрессионного разложения временного сигнала, позволяющая для входного сигнала типа «меандр» получать регулярным образом достоверные оценки его амплитуды и длительности.

Литература

1. Визильтер Ю.В., Лагутенков А.В., Ососков М.В., Выголов О.В., Блохинов Ю.Б. Выделение и межкадровое прослеживание движущихся объектов при регистрации изображений сложных пространственных сцен произвольно движущимися двумерными сенсорами // Вестник компьютерных и информационных технологий. 2006. № 3. С. 34-38.

2. Вишняков Б.В., Визильтер Ю.В., Лагутенков А.В. Использование модифицированного метода оптических потоков в задаче обнаружения и межкадрового прослеживания движущихся объектов // Вестник компьютерных и информационных технологий. 2007. № 5. С. 2 – 8.

3. Barron J.L., Fleet D.J., Beauchemin S.S. Performance of optical flow techniques // Internat. Jour. of Computer Vision. 1994. 12(1). Р. 43–77.

4. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. М.: ИНФРА-М, 2003. 544 с.

5. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и Управление. М.: Мир, 1974. 608 с.