Волченко Е.В. - О способе определения близости объектов взвешенных обучающих выборок

Аннотация

В работе предложена метрика для определения расстояния между объектами обучающих выборок, имеющими вес. Выполнено расширение алгоритма k-ближайших соседей на взвешенные выборки w-объектов с вычислением расстояния на основе предложенной метрики. Проведены экспериментальные исследования, подтвердившие эффективность предложенного подхода

Постановка проблемы и анализ литературы

Классификация объектов в обучающихся системах распознавания заключается в определении их близости к объектам обучающей выборки на основе выбранной метрики (функции расстояния).

Метрикой называют неотрицательную вещественную функцию d(X_i, X_j), удовлетворяющую следующим условиям [1]:

d(X_i, X_j)≥0 для всех объектов X_i и X_j обучающей выборки X;
d(X_i, X_j)=0 тогда и только тогда, когда X_i = X_j(аксиома тождества);
d(X_i, X_j)=d(X_j, X_i)(аксиома симметрии);
d(X_i, X_j)≤d(X_i, X_s)+d(X_s, X_j) где X_i, X_j и X_s – три любые объекта выборки X (аксиома треугольника).

Особенности расположения объектов обучающей выборки в признаковом пространстве, недостаточный (избыточный) объем данных, наличие шума и неполных данных существенно повышают важность выбора метрики, позволяющей выполнять классификацию объектов с наибольшей эффективностью [2]. На сегодняшний день разработано значительное количество метрик, перечень которых можно найти, например, в [3], обеспечивающих высокую эффективность классификации, однако для некоторых видов систем распознавания этот вопрос остается открытым.

Анализ большого числа прикладных задач, решающихся путем построения систем распознавания показал, что на сегодняшний день наиболее востребованными являются адаптивные обучающиеся системы распознавания, характеризующиеся способностью изменять свои свойства (словарь признаков, обучающую выборку, решающие правила классификации и т.д.) в соответствии с изменениями распознаваемых объектов [4]. Определяющей особенностью этих систем является возможность пополнения обучающей выборки новыми объектами на всем протяжении времени работы системы, что приводит к неограниченному росту обучающей выборки и необходимости корректировки решающих правил при добавлении новых объектов.

В предыдущих работах автора [4, 5] для сокращения размера обучающих выборок в адаптивных обучающих системах была предложена и реализована алгоритмически идея перехода к взвешенным обучающим выборкам, каждый w-объект которой строится по множеству близкорасположенных в пространстве признаков объектов исходной выборки. Значения признаков w-объектов являются центрами масс значений признаков объектов найденных множеств. Вес содержит информацию о взаиморасположении, количестве или качестве заменяемых объектов и, исходя из результатов экспериментальных исследований, проведенных в предыдущих работах, позволяет существенно повысить эффективность работы систем

Введение дополнительной характеристики для описания w-объектов не позволяет корректно выполнять классификацию объектов из-за отсутствия метрики, рассчитывающей расстояние между объектами, имеющими разный вес.

Цель работы

Целью данной работы является разработка и анализ метрики для оценки степени близости объектов во взвешенных обучающих выборках.

Постановка задачи

Пусть имеется некоторая конечная взвешенная обучающая выборка w-объектов X^W={X₁^W, X₂^W,...,X_k^W}. Каждый w-объект X_i^W этой выборки описывается системой признаков {X_i1, X_i2,...,X_in} и весом p_i – целым положительным числом, т.е. X^W={X₁^W, X₂^W,...,X_k^W, p_i} и представляется точкой в линейном пространстве признаков, т.е. X_i∈Rⁿ. Для каждого w-объекта известна его классификация y_i∈V, где V={V₁,...,V_l} – множество всех классов системы.

Имеется некоторый объект X_s={X_s1, X_s2,...,X_sn} , заданный только набором признаков (для единообразия присвоим ему вес равный единице, т.е. p_s=1, тогда X_s^W={X_s1^W, X_s2^W,...,X_sn^W, p_s}).Необходимо выполнить классификацию объекта X_s^W для чего требуется построить функцию d_W(X_s^W, X_i^W) оценки расстояния между классифицируемым объектом и объектами взвешенной обучающей выборки.

Построение метрики на взвешенных обучающих выборках

Выбор метрик в задачах распознавания ограничивается, в первую очередь, сложностью их вычисления [6] и близостью к реальному топологическому разделению пространства признаков на области, соответствующие классам системы [7].

По результатам анализа особенностей расположения объектов взвешенной выборки в пространстве признаков может быть предложена следующая метрика.

Пусть каждый w-объект взвешенной обучающей выборки представляется материальной точкой в признаковом пространстве Rⁿ и имеет массу, равную весу w-объекта.

Тогда "близость" двух материальных точек (двух w-объектов) X_i^W={X_i1, X_i2,...,X_in, p_i} и X_j^W={X_j1, X_j2,...,X_jn, p_j} в пространстве признаков может быть определена по силе притяжения между ними

Два w-объекта X_i^W и X_j^W являются ближайшими, если сила притяжения между ними, рассчитанная по формуле (1), максимальна.

Поскольку при вычислении расстояний два объекта являются ближайшими, если расстояние между ними минимально, в качестве метрики для определения расстояния между w-объектами будем использовать величину, обратную к (1).

Теорема

Функция является метрикой

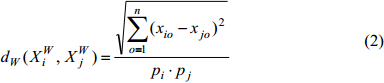
Доказательство. Покажем, что формула (2) определяет метрику, т.е. удовлетворяет условиям 1 – 4.

Свойство 1. Для любой пары w-объектов X_i^W и X_j^W взвешенной обучающей выборки X^W d_W(X_i^W, X_j^W)≥0.

В формуле (2) выражение является евклидовой метрикой, для которой данное свойство выполняется. Согласно постановке задачи веса w-объектов p_i≥1 и p_j≥1, поэтому для (2) свойство 1 выполняется для любых X_i^W и X_j^W.

Свойство 2. Для любой пары w-объектов X_i^W и X_j^W взвешенной обучающей выборки X^W d_W(X_i^W, X_j^W) = 0 тогда и только тогда, когда X_i^W = X_j^W.

Пусть x_io = x_jo для всех o=1,n, тогда

(по условию p_i≥1 и p_j≥1), т.е. для (2) свойство 2 выполняется для любых X_i^W и X_j^W.

Свойство 3. Для любой пары w-объектов X_i^W и X_j^W взвешенной обучающей выборки X^W d_W(X_i^W, X_j^W) = d_W(X_j^W, X_i^W).

Поскольку

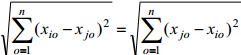
то, свойство 3 выполняется для любых X_i^W и X_j^W.

Свойство 4. Для любых w-объектов X_i^W, X_j^W и X_k^W выборки X^W d_W(X_i^W, X_j^W)≤d_W(X_i^W, X_k^W)+d_W(X_k^W, X_j^W).

Рассмотрим естественный случай, когда выполняется расчет расстояния от двух w-объектов X_i^W, X_j^W (обычно принадлежащих разным классам) до распознаваемого объекта X_s^W, т.е. покажем, что d_W(X_i^W, X_j^W)≤d_W(X_i^W, X_s^W)+d_W(X_s^W, X_j^W).

Пусть

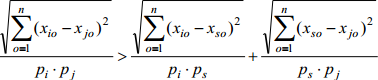
В результате преобразований получим выражение

Так как p_s=1, а p_i≥1 и p_j≥1, то неравенство (3) является неверным и свойство 4 выполняется для любых X_i^W, X_j^W и классифицируемого объекта X_s^W.

Отметим, что рассмотрение случая, когда классифицируемый объект X_s^W имеет неединичный вес, будет рассмотрено в следующих работах.

Классификация объектов на основе взвешенных обучающих выборок

Для классификации объектов на основе взвешенных обучающих выборок w-объектов будем использовать алгоритм k-ближайших соседей [2], широко применяющийся при решении задач классификации в условиях неполных априорных данных. Выбор данного метода для классификации на основе взвешенной обучающей выборки основывается на результатах исследований [5], согласно которым он будет показывать высокую эффективность классификации при использовании сокращенной обучающей выборки. Для классификации объекта X_s^W с помощью метрики (2) найдем k ближайших к нему w-объектов каждого из классов и отнесем к тому классу, суммарное расстояние до объектов которого минимально.

Результаты экспериментальных исследований

Для оценки эффективности предложенного подхода был проведен ряд экспериментальных исследований. В качестве исходных данных были использованы выборки объектов двух классов размером 1000 – 5000 объектов при 20% пересечении областей классов в пространстве признаков, содержащих 5 – 20 признаков распознавания. Для генерации значений признаков использовался нормальный и равномерный законы распределения.

Оценка эффективности классификации объектов на основе взвешенной обучающей выборки по предложенной модификации алгоритма k-ближайших соседей выполнялась на тестовых выборках размером 100 объектов, полученных с помощью тех же генераторов, что и обучающие выборки. В качестве критерия оценки эффективности классификации использовалась частота неверных классификаций. Количество "ближайших соседей" равно 10% размера обучающей выборки w-объектов.

Анализ полученных результатов позволяет сделать следующие выводы:

1. Pазмер взвешенной выборки w-объектов составил в среднем 2,3% размера исходной обучающей выборки;

2. Частота неверной классификации объектов тестовой выборки модифицированным методом k-ближайших соседей по выборке w-объектов уменьшилась в среднем на 7,4% по сравнению с частотой неверной классификации методом k-ближайших соседей по исходной выборке.

Отметим, что близкие результаты были получены при 10 – 40% пересечении областей классов в пространстве признаков и изменении количества признаков распознавания.

Также были проведены экспериментальные исследования эффективности предложенного подхода на выборках репозитория ISEC (International Statistical Education Centre) [9], для которых частота неверной классификации объектов модифицированным методом k-ближайших соседей по выборке w-объектов уменьшилась в среднем на 5,3%.

Выводы

В работе предложен способ оценки расстояния между объектами взвешенной обучающей выборки и классифицируемыми объектами с помощью новой метрики. Выполнено расширение алгоритма k-ближайших соседей на взвешенные выборки w-объектов с вычислением расстояния на основе предложенной метрики.

Результаты экспериментальных исследований показали устойчивое уменьшение частоты неверных классификаций в среднем на 7,4%, что позволяет сделать вывод об эффективности использования взвешенных выборок w-объектов в адаптивных обучающихся системах.

Автор благодарит к.ф.-м.н., с.н.с. И.С. Грунского за ряд ценных замечаний и внимание к данной работе.

Список использованной литературы

1. Дюран Б. Кластерный анализ / Б. Дюран, П. Оделл. – М.: Статистика, 1977. – 130 с. 2. Theodoridis S. Pattern Recognition / S. Theodoridis, K.Koutroumbas. – San Diego: Academic Press, 2008. – 823 p. 3. Воронин Ю.А. Теория классифицирования и её приложения / Ю.А. Воронин. – Новосибирск: Наука, 1985. – 232 с. 4. Розробка теоретичних засад i методів реалiзацiї відкритих систем автоматичного розпізнавання, що навчаються: способи оптимiзацiї навчаючих вибiрок i методи побудови зважених вирішуючих правил класифiкацiї [Текст]: звiт з НДР (заключний): Тема GP/F32/130, Грант Президента України для пiдтримки наукових дослiджень молодих учених на 2011 рiк / керiвник роботи О.В. Волченко. – Донецк, ГВУЗ "ДонНТУ", 2011. – 67 с. 5. Волченко Е.В. Метод построения взвешенных обучающих выборок в открытых системах распознавания / Е.В. Волченко // Доклады 14-й Всероссийской конференции "Математические методы распознавания образов (ММРО-14)", Суздаль, 2009. – М.: Макс- Пресс, 2009. – С. 100 – 104. 6. Гороховатский В.А. Метрики на множествах ключевых точек изображений / В.А. Гороховатский // Бионика интеллекта. – 2008. – № 2 (69). – С. 45 – 50. 7. Рудаков К.В. О структуре метрических технологий Data Mining / К.В. Рудаков, Г.В. Никитов // Искусственный интеллект. – 2002. – № 2. – С. 218 – 220. 8. Павлов Д.А. Модифицированный алгоритм классификации типа k-ближайших соседей / Д.А. Павлов, А.П. Серых // Фундаментальная и прикладная математика. – 2000. – Том 6. – № 2. – С. 533- 548. 9. http://www.isical.ac.in/~miu

Статью представил д.ф.-м.н. доц., зав. кафедрой системного анализа и моделирования Института информатики и искусственного интеллекта ГВУЗ "ДонНТУ" Миненко А.С.