Деменко А. Г., Зінченко Ю. Є. - Зондове діагностування слабопослідовних схем за методологією «веденого зонда»

Введення

Важливою складовою експлуатації обчислювальної техніки завжди було технічне обслуговування, зокрема діагностування, пошук та усунення несправностей. На даний час в сучасних цифрових пристроях все частіше застосовується контролепридатне проектування, яке дозволяє автоматизувати тестування і пошук несправностей.

Для широкого застосування діагностики необхідний оптимальний алгоритм пошуку несправностей (АПН), але його немає. Це пояснюється трудомісткістю та складністю розробки таких алгоритмів. В галузі систем зондової діагностики (ЗД) залишається невирішеним ряд проблем, серед яких в першу чергу слід виділити проблеми мінімізації перестановок зонда (тобто тривалості процесу діагностики), локалізації несправності з точністю до знімною компоненти та проблему мінімізації зовнішньої пам’яті системи ЗД.

Актуальним є пошук рішень цих проблем з метою отримання досить універсального алгоритму пошуку несправностей.

Мета роботи – розробити алгоритм зондового пошуку несправностей для цифрових схем, з урахуванням технологічних особливостей «реальних» схем, та оптимізувати його по середній кількості перестановок зонда [1].

1 Граф пошуку несправностей за методологією «веденого зонда»

Метод пошуку несправності (МПН), який реалізує алгоритм пошуку несправності (АПН), використовує граф пошуку несправностей (ГПН), що визначає послідовність зондування ключових точок (КТ), залежно від стану схеми [1-2]. Граф пошуку несправності будується за описом схеми.

Вершини ГПН підрозділяються на чотири типи: початкову, проміжні, контрольні і кінцеві. Мітки початкової, проміжних і контрольних вершин складаються з одного елементу і є символічними позначеннями КТ, які перевіряються в процесі зондування. Початкова вершина символізує КТ (контакт вихідного або двонаправленого роз’єму), в якій була вперше зафіксована несправність ОД і в підсхемі якої виконуватиметься пошук несправності. Проміжні вершини позначають КТ, які необхідно прозондувати. Контрольні вершини використовуються для запам’ятовування інформації про те, що КТ вже була прозондована, що дозволяє виявити кільця в схемі, в яких неможливо встановити несправний елемент. Якби контрольні вершини були відсутні, то складно було б визначити, що КТ вже зондувалася, оскільки довелося б шукати всі проміжні вершини з однаковими мітками і позначати їх. Кінцева вершина графа символізує закінчення пошуку несправності по одній з гілок графа; мітка вершини містить повідомлення, яке описує припущено джерело несправності, виражене множиною з одного або декількох елементів ОД. Множина міток контрольних вершин співпадає з множиною міток проміжних вершин. Ця множина складається з символічних позначень всіх КТ схеми. Кожної КТ відповідає рівно одна контрольна вершина, а відповідних проміжних вершин може бути декілька [3].

З проміжних вершин ГПН завжди виходитимуть дві дуги, помічені символом R1 = ‘N’ і R2 = ‘Y’, ототожнювані з результатом зондування КТ, відповідній даній вершині. Дуга з міткою ‘Y’ позначає перехід у разі збігу реальної ТР КТ з еталонною, дуга з міткою ‘N’ - перехід у разі неспівпадання реакцій. По дузі з міткою ‘Y’ можна перейти в іншу проміжну або в кінцеву вершину. По дузі з міткою ‘N’ завжди виконується перехід в контрольну вершину, мітка якої співпадає з міткою проміжної вершини. Початкова і контрольна вершини завжди мають одну витікаючу дугу з міткою ‘N’, по якій виконується перехід в проміжну або кінцеву вершини. Дуги з міткою ‘Y’ називаються Y-дугами, а з міткою ‘N’ – N-дугами.

Послідовність вершин ГПН, зв’язана дугами, що починається початковою вершиною і закінчується однією з кінцевих вершин, символізує порядок зондування контрольних точок ОД за наявності в останньому несправності, описуваною кінцевою вершиною і при виникненні в ньому ТР, описуваних відповідними дугами. Кількість проміжних вершин такої послідовності відображає число перестановок зонда, яке необхідно здійснити для виявлення несправності, описуваною кінцевою вершиною послідовності. Граф в цілому задає алгоритм пошуку всіляких несправностей ОД [2].

ГПН може бути легко представлений для машинної обробки. У системі ЗД такий граф можна задавати за допомогою текстового файлу, для чого розроблений спеціальний формат структури файлу. Експериментальні дослідження показали, що розмірність такого файлу порівняно не висока і пов’язана з об’ємом ОД прямо-пропорційною залежністю [3].

Основною характеристикою АПН є середнє число перестановок зонда (матема- тичне очікування), яке необхідно виконати для виявлення середньостатистичної несправності ОД. Ця характеристика може бути легко розрахована за допомогою ГПН, що також є одним з його достоїнств.

Використання ГПН в представленій інтерпретації по суті зумовлює в цілому стратегію пошуку несправностей об’єкту ЗД [3-4].

2 ГПН для комбінаційної схеми

Схема, що діагностується, складається з чотирьох компонент (рис. 1). Схема є комбінаційною (КС) або слабопослідовною (псевдокомбінаційною – ПКС), оскільки в ній відсутні глобальні зворотні зв’язки. В алгоритмі «веденого зонда» використовується опис тільки структури схеми, а функціональність, реалізована кожним компонентом, значення не має. Компоненти схеми та їх виходи пронумеровані. Вхідні і вихідні псевдокомпоненти позначаються великими літерами [4].

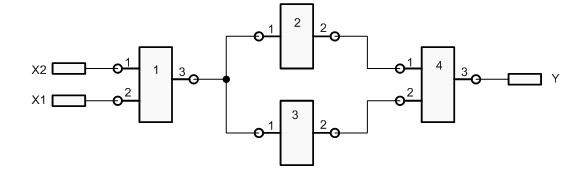
Рисунок 1. Схема, що діагностується

На рис. 2 приведений ГПН для наданої схеми. Вершини позначені кухлями, усередині яких знаходяться мітки. Ребра позначені стрілками, їх мітки пишуться поряд. Початкова і контрольні вершини обведені, щоб відрізняти їх від проміжних і кінцевих вершин. У якості мітки проміжних і контрольних вершин використовуються номер компонента і номер його виводу, розділені через крапку, що однозначно визначає КТ схеми. Початкова вершина як мітку має позначення вихідного псеводокомпонента. У кінцевих вершинах, якщо несправний компонент, ставитися буква ‘К’ і номер компоненту, а якщо несправна ЛС, то буква ‘Л’ і мітка КТ, до якої дана ЛС підключена.

3 ГПН для слабопослідовної схеми

У роботі запропонований поліпшений АПН за методологією «веденого зонда», зокрема, з можливістю виділення з об’єкта діагностики блоків з локальними зворотними (замкнутими) зв’язками. Це, в свою чергу, дозволить сприймати групу елементів з локальними зворотними зв’язками як псевдоелемент. Таким чином, ОД буде псевдокомбінаційною, а не складно- або слабопослідовною схемою.

Для наочності розглянемо приклад на рис. 3. Наведена комбінаційна схема подібна до схеми на рис. 1, але в ній замість елемента 2 розташований RS-тригер. Тригер складається з елементів 5 та 2 - групи елементів, які мають локальні зворотні зв’язки. Схема є слабопослідовною. Її можна перетворити на псевдокомбінаційну, замінивши тригер на еквівалентний псевдоелемент, що виконує аналогічну функцію. Отримана псевдокомбінаційна схема буде аналогічною до схеми з рис. 1, її ГПН - аналогічним до рис. 2. Він є значно простішим та вимагає меншу кількість перестановок зонду, ніж складний ГПН для схеми з рис. 3.

Для пошуку несправності в отриманій псевдокомбінаційній схемі можна застосувати алгоритм GALOP, який вимагає меншу кількість перестановок зонда, ніж SCAN, що застосовується у схемах зі зворотними зв’язками. Якщо несправність була виявлена в псевдоелементі, то очевидно, що вона в групі елементів зі зворотними зв’язками. Для цієї групи буде застосовуватися вже алгоритм SCAN.

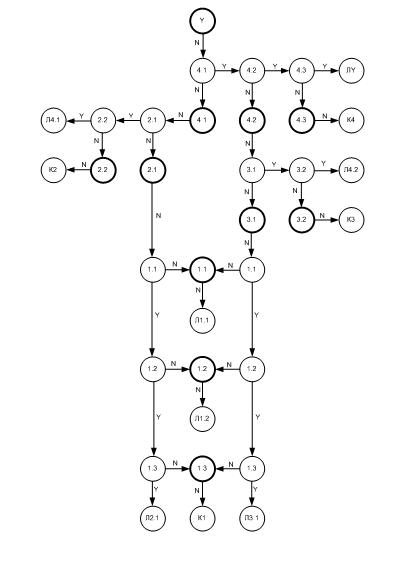
Рисунок 2. ГПН для схеми, що діагностується

Рисунок 3. Слабопослідовна схема, що діагностується

Висновки

Робота в позначеному напрямку пов’язана з розробкою і тестуванням АПН по методу «веденого зонда», з особливою увагою до пошуку і заміні груп елементів з локальними зворотними зв’язками на еквівалентні псевдоелементи.

Був розгянутий приклад побудування ГПН як для слабопослідовної схеми, так і для аналогічної псевдокомбінаційної. Необхідна подальша розробка та тестування АПН на реальних схемах.

Якщо розроблений алгоритм буде досить вдалим, то його використання в ЗД принесе значну вигоду в часі тестування обчислювальних пристроїв, інтегральних схем та іншої техніки, що потребує діагностики.

Литература

Малышко, Ю.В., Чипулис, В.П., Шаршунов, С.Г. Автоматизация диагностирования электронных устройств [Текст] / Ю.В. Малышко, В.П. Чипулис, С.Г. Шаршунов. // Москва : Энергоатомиздат, 1986. – 216 с.
Горяшко, А.П. Синтез диагностируемых схем вычислительных устройств [Текст] / А. П. Горяшко // Москва : Наука, 1987. – 288 с.
Зинченко, Ю.Е., Козинец, А.М., Жилин, К.Н. Проблемы зондового поиска неисправностей и пути их разрешения [Текст] / Ю.Е. Зинченко, А.М. Козинец, К.Н. Жилин // Сборник трудов Донецкого государственного технического университета. Серия: Информатика, кибернетика и вычислительная техника, выпуск 6. – Донецк : ДонГТУ, 1999. – С. 212-217.
Деменко, А.Г., Ханаев, В.В., Зинченко, Ю. Е., Зинченко, Т. А. Проблемы минимизации количества перестановок зонда в процессе поиска неисправностей по методологии «ведомого зонда» [Текст] / Деменко А.Г., Ханаев В.В., Зинченко Ю.Е., Зинченко Т.А. // Сборник трудов III научно- технической конференции студентов, аспирантов и молодых ученых – 16-18 апреля 2012 г. – Донецк : ДонНТУ, 2012.

Назад в библиотеку