Назад в библиотеку

Ініціалізація як етап тестування цифрових схем

Автор: Мяделец О.О., Зінченко Ю.Є.
Источник:

В цій доповіді розповідається про поняття ініціалізації послідовних схем, а також про зв'язок цього поняття з тестуванням цифрових пристроїв.

По визначенню послідовної схеми, майбутня її поведінка залежить від поточного стану. Таким чином, тестова послідовність (послідовність, яка тестує схему) повинна бути застосована до ініціалізованної схеми [1]. Коли схема включена, вона перебуває в невизначеному стартовому стані. Цей стартовий стан може бути відмінним для кожного зразка схеми; для тої ж самої схеми, кожне включення електроживлення не веде до однакового стартового стану. Перш, ніж тестова послідовність буде застосована до такої схеми, її установлюють у відомий стан послідовністю ініціалізації (предустановочною послідовністю), протягом якої, послідовність на виході не важлива. Після послідовності ініціалізації схема перебуває в початковому стані. Це показано на рисунку 1.

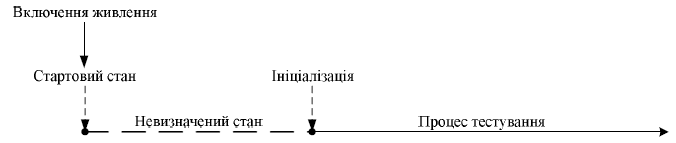
Початковий стан і стан ініціалізації

Рис. 1. Початковий стан і стан ініціалізації

Коректно працюючі схеми з різними початковими станами можуть мати різні вихідні дані. Тому очікувана відповідь справного контуру не буде унікальною, якщо ініціалізація не була виконана. Тому ініціалізація особливо важлива, коли тестування складається в порівнянні реакції схеми, що тестується, з реакцією еталонної схеми (звичайно так проводиться детерміноване й псевдовипадкове тестування) [3]. Фактично всі цифрові схеми можуть бути ініціалізованими одним з методів, які будуть наведені нижче.

Початковий стан справного контуру визначається винятково послідовністю ініціалізації [2]. Але з іншого боку, початковий стан дефектного контуру не обов'язково є унікальний й може бути невідомим, навіть якщо послідовність ініціалізації відома. Однак, деякі тестові методи не беруть цей факт до уваги, припускаючи, що початкові стани дефектного й справного контурів однакові. Це е недоробкою таких методів, бо про несправність контуру можна судити вже після невірної ініціалізації.

У деяких випадках послідовність ініціалізації представляє тільки зовнішнє скидання, що не розглядається як вхід автомата, що описує схему. Якщо в контурі існує скидання при вмиканні живлення, тоді говорять, що вхідна послідовність нульової довжини. Це є специфічний випадок послідовності ініціалізації (початковий стан є стартовим станом - схема є такою, що ініціалізується самостійно).

Таким чином, існують 3 види ініціалізації:

  1. скидання при включенні живлення;
  2. зовнішнє скидання;
  3. синхронізуюча послідовність.

Для першого й другого видів, початковий стан q0 є унікальним й не може бути обраний користувачем [1].

Для третього виду користувач може вибирати початковий стан. Однак у цьому випадку автомат, який описує схему, повинен бути сильнозв'язаним, тобто:

  1. будь-який "корисний" стан повинен бути доступним з будь-якого іншого;
  2. стан q0, обраний початковим станом, повинен бути досягнутим з будь- якого стартового стану;
  3. удь-який стан, що не може бути досягнутий з q0, не є "корисним".

Виходячи з вище наведеного, можна зробити наступні висновки.

  1. З попередніх зауважень, що стосуються ініціалізації, прямує, якщо автомат не є сильнозв'язаним, то скидання повинно бути або по включенню живлення, або зовнішнім.
  2. Автомат із зовнішнім скиданням може бути представлений як сильнозв'язаний автомат із синхронізуючою послідовністю шляхом додавання лінії скидання на вході.
  3. Послідовність синхронізації - це вхідна послідовність, що переводить схему у відомий стан ініціалізації з будь-якого стартового стану.
  4. Схема без скидання по включенню живлення або без зовнішнього скидання, і яка не має послідовності синхронізації існувати може. Наприклад, дільник частоти на 2. Деякі автори затверджують, що така схема не придатна для ініціалізації. Однак вона може бути ініціализованою з використанням установчої послідовності.
  5. Вхідна послідовність Sh називається установчою, якщо кінцевий стан автомата (тобто після подачі Sh) може бути визначеним однозначно з реакції схеми на Sh незалежно від стартового стану (тобто того, який був до подачі Sh).
  6. Якщо схема з несправністю не виробляє одну з очікуваних відповідей на установчу послідовність, несправність такої схеми відразу виявляється.
  7. Існує необхідність у розробці алгоритму, що дозволяє встановити схему в визначений стан з будь-якого початкового, за мінімальну кількість вхідних векторів.

Литература

  1. Rene David. Random Testig of Digital Circuits. Theory and Applications. Marcel Dekker, Inc, 2000, - 475c.
  2. Agrawal V.D. Essentials of electronic testing for digital, memory and mixedsignal VLSI circuits/ Kluwer Academic Publishers, 2000, - 690c.
  3. Хаханов В.И. Техническая диагностика цифровых и микропроцессорных структур: учебник. K. ИСИО, 1997.- 242с.
Назад в библиотеку