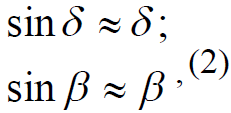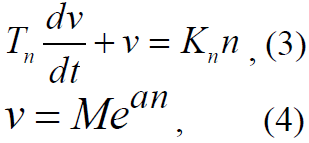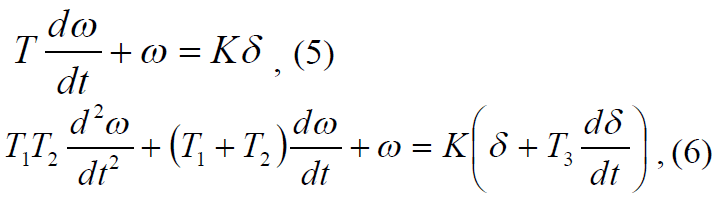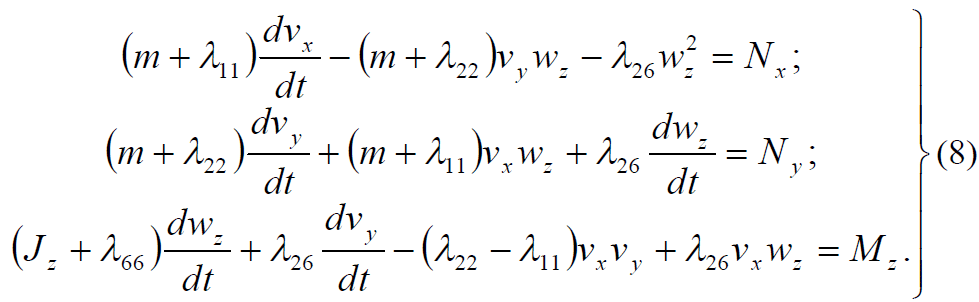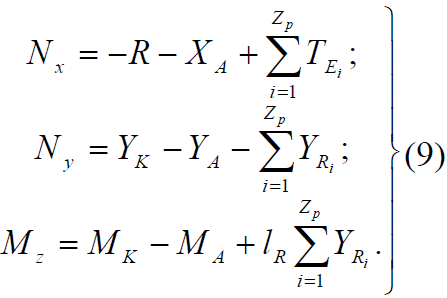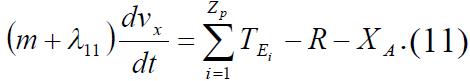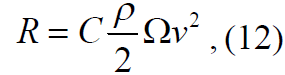Аноприенко А.Я., Кривошеев С.В. – Моделирование динамики движения речного судна на базе системы MATLAB/SIMULINK

Введение

Компьютерное моделирование в настоящее время стало важнейшим инструментом для изучения динамического поведения технических систем. Вместо создания опытного дорогостоящего образца для исследования особенностей динамики новой системы согласно проекту, может быть составлена ее математическая модель. При этом предполагается реализация разработанной модели в некоторой среде моделирования, позволяющей произвести требуемый анализ динамических характеристик: стабильности, времени реакции, точности выполнения задачи и т.д.

Увеличение скорости и плотности транспортных потоков, необходимость перевозки опасных грузов и прочие причины привели к тому, что в настоящее время проблемы увеличения безопасности движения являются актуальными и первостепенными. Аварии на транспортных потоках приводят к гибели людей и загрязнению окружающей среды, что приводит к огромным экономическим потерям. Одним из способов решения проблем данного направления является создание автономных автоматических транспортных средств [1, 2]. Необходимым условием при этом является наличие навигационной системы в контуре управления.

В качестве примера рассмотрим интегрированную навигационную систему (ИНС) для судов внутреннего и смешанного плавания [3]. Основной задачей данной системы является автономное управление движением по заданному маршруту речного судна с учетом реальной навигационной обстановки.

1. Компоненты навигационной системы

В составе ИНС выделяют четыре основных компонента [3]: бортовые датчики, база априорных знаний, исполнительные механизмы и бортовой вычислительный комплекс. Назначение бортовых датчиков – предоставление информации о реальной навигационной обстановке. Однако информация от бортовых датчиков поступает с определенной задержкой, а также зависит от типа датчика.

Например, радиолокационное изображение [4] ландшафта навигации поступает от радиолокационной станции приблизительно каждые 2,2 секунды при скорости вращения антенны 26 оборотов в минуту. Измерение скорости судна осуществляется с помощью лага. Погрешность измерений для данного прибора колеблется в пределах 5-10%, а также зависит от градиента дна. Измерение скорости с помощью приемника спутниковой навигационной системы увеличивают точность измерений, но при наличии мощных источников электромагнитных излучений достоверность информации существенно снижается.

Для определения курса судна используют гирокомпас, результаты измерений которого также зависят от инерционности прибора.

Таким образом, для обеспечения удержания судна на заданной траектории необходимо обеспечить высокую точность измерений параметров движения, в т.ч. скорости и курса.

2. Математическая модель судна

Основными параметрами движения судна являются скорость v движения и курс Ψ судна. Уравнение для вычисления курса судна имеет следующий вид [5]:

где ω – угловая скорость вращения.

При выполнении судном «слабых» маневров,

где δ – угол перекладки руля, β – угол дрейфа [5], уравнения для расчета скорости судна можно записать в одном из следующих видов:

где T_n, K_n – нелинейные коэффициенты, зависящие от числа оборотов двигателя; n – число оборотов двигателя; M, a – постоянные коэффициенты.

Коэффициенты, входящие в уравнение (4) можно рассчитать по результатам ходовых испытаний с помощью метода наименьших квадратов.

Закон управления судном, при выполнении условия (2), обычно описывают одним из следующих уравнений Номото [6]:

где K – коэффициент, определяемый характеристиками судна (формой, размерами, параметрами движения); T_i (i=1,2,3) в уравнении (6) – постоянные времени [6]. Постоянная времени T в уравнении (5) вычисляется по формуле:

T=T₁+T₂−T₃. (7)

Уравнение (6) применяется для более точного описания угловой скорости вращения и наличии высокопроизводительных средств вычислений. Уравнение (5) используется при жестких ограничениях на время вычисления, а также для предсказания значений скорости вращения судна.

При выполнении судном «сильных» маневров условие (2) не выполняется и результаты вычислений параметров движения по формулам (3)–(7) являются приближенными. Один из способов получения точных результатов измерений заключается в уточнении данных на основе информации, поступающей от бортовых датчиков. Другой способ – это применение более точной математической модели описания параметров движения судна.

Из анализа формул (3) и (4) видно, что для судов, оборудованных одновальной силовой установкой, скорость можно рассчитать при любых режимах работы двигателя на переднем ходу. Для судов с двухвальной силовой установкой скорость по уравнениям (3) и (4) рассчитывается при условии работы обоих винтов в одинаковых режимах.

При использовании следующей модели [5] можно описать все возможные маневры судна в горизонтальной плоскости:

где λ_ij – обобщенные присоединенные массы корпуса судна, образуемые водной средой, в которой осуществляется движение; m – масса судна; J_z – присоединенный момент инерции массы судна; v_x, v_y, – проекции вектора скорости судна (рис. 1); ω_z – проекция на ось Z вектора угловой скорости движения судна; N_x, N_y, – проекции вектора внешних сил; M_z – проекции вектора главного момента.

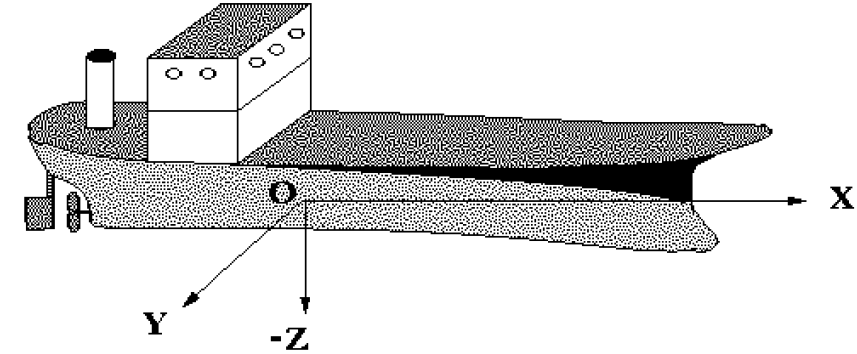
Рис. 1. – Система координат судна

В системе уравнений (8) в явном виде не показано влияние режимов работы двигателей на параметры движения. Для явного указания влияния режимов работы двигателей распишем формулы для проекций сил и момента [5]:

где R – сопротивление воды движению судна; Y_K – боковая гидродинамическая сила; M_K – момент гидродинамических сил относительно вертикальной оси; X_A, Y_A – проекции аэродинамической силы на ось x и y соответственно, M_A – момент аэродинамических сил, T_Ei, Y_Ri – полезная тяга и боковая сила i-го движительно-рулевого комплекса (ДРК); Z_p – число ДРК; l_R – расстояние от ДРК до центра тяжести судна.

Сила тяги пропорциональна плотности воды ρ, частоте вращения винта n и диаметру винта D [5]:

T_Ei=k_Tρn²D⁴, (10)
где k_T – коэффициент упора винта.

При неустановившемся прямолинейном движении судна скорость можно рассчитать по следующей формуле [5]:

Структура формулы для сопротивления воды движению судна, вытекающая из теории подобия движений жидкости, имеет следующий вид:

где Ω – площадь, погруженного в среду, тела; C – коэффициент полного сопротивления.

3. Реализация модели судна

Для изучения влияния режимов работы ДРК на параметры движения была создана модель в среде моделирования SIMULINK, которая позволяет создавать иерархические структуры моделей с неограниченной вложенностью и собственные библиотеки блоков. Этот пакет обеспечивает также непосредственный доступ к математическим, графическим и программным средствам системы MATLAB.

Для уравнений (1), (3)–(6), (8), (9)–(12) была составлена блок-схема модели в среде SIMULINK. На рис. 2 представлена в качестве примера схема для расчета сопротивления воды движению судна.

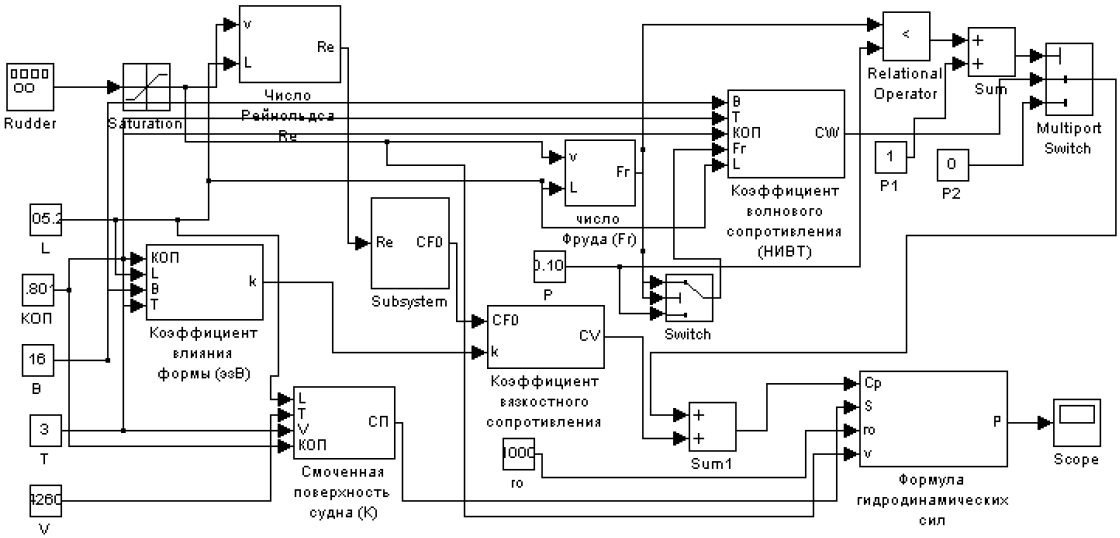
Рис. 2. – Схема для расчета сопротивления воды движению судна

Для исследования различных режимов движения судна изменяются угол перекладки руля и скорость вращения винтов.

Приведенная математическая модель является частью модели, используемой для планирования траектории движения судна и управления движением судна по ней.

Заключение

Гибкость системы моделирования SIMULINK, а также возможность изменения параметров моделирования динамического объекта, позволяет исследовать различные режимы работы силовой установки судна, а также параметры движения. Результаты решения системы дифференциальных уравнений, которые составляют математическую модель силовой установки и динамики судна, позволяют планировать траекторию движения управляемого объекта, обеспечивать его оптимальное управление, а также осуществлять фильтрацию входных сигналов от бортовых датчиков и уточнять их значения. Рассмотренная математическая модель и ее реализация являются элементом среды моделирования интегрированной навигационной системы судов внутреннего и смешанного плаваний [7]. Данная работа выполняется в рамках договора о научном сотрудничестве ДонГТУ с Институтом системной динамики и управления (ISR) Штуттгартского университета (Германия).

Литература

Bertozzi M., Broggi A. Vision-based vehicle guidance. //Computer, 30 (1997), №7, p.49-55.
Sandler M., Wahl A., Zimmermann R., Faul M., Kabatek U. and Gilles E.D. Autonomous guidance of ships on waterways. Robotics and Autonomous Systems 18 (1996), p.327-335.
Кривошеев С.В., Потапенко В.А. Подходы к моделированию работы интегрированных навигационных систем для судов внутреннего и смешанного плавания //Наукові праці Донецького державного технічного університету. Серія: Інформатика, кібернетика та обчислювальна техніка, вип. 6. – Донецк: ДонДТУ. – 1999. С.115-120.
Святный В.А., Аноприенко А.Я., Кривошеев С.В., Потапенко В.А. Имитация радиолокационной информации в интегрированной навигационной системе //Сборник трудов VI международной научно- технической конференции «Машиностроение и техносфера на рубеже XXI века. – Том 3. – Донецк. – 1999. – с.12-15.
Ходкость и управляемость судов. Под ред. В.Г. Павленко. М.: Транспорт, 1991. – 396 с.
Nomoto K. On steering quality of ships, International Shipbuilding Progr. 4 (35) (1957) pp.354-370.
Аноприенко А.Я., Кривошеев С.В. Разработка подсистемы моделирования движения судна по заданной траектории // Научные труды Донецкого национального технического университета. Выпуск 12. Серия «Вычислительная техника и автоматизация». – Донецк, ДонГТУ, ООО «Лебедь», 1999. С. 197-202.