Динамическое нечеткое управление с блоком на основе нейронной сети
Автор: Mehmet KARAKОSE, Erhan AKIN
Источник:http://www.emo.org.tr/ekler/6dcd52497101933_ek.pd
Автор: Mehmet KARAKОSE, Erhan AKIN
Источник:http://www.emo.org.tr/ekler/6dcd52497101933_ek.pd
В данной работе рассмотрены различные нечеткие алгоритмы управления, который использует динамическую систему нечеткой логики, основанную на нейронной сети. Эти методы предлагается для решения динамических задач управления. Предлагаемый алгоритм является общим методом, который может быть применен к большому разнообразию реальных мировых проблем. Эффективность предлагаемого метода иллюстрируется результатами моделирования для задачи управления положения двигателя.
Динамическая нечеткая система, блок на основе нейронной сети, нечеткое управление.
Нечеткая логика в течении последние два десятилетия привлекла большое внимание как мощный инструмент для контроля многих систем [1]. Системы, разработанные с использованием нечеткой логики, реализуют человеческие рассуждения, запрограммированные в виде функций принадлежности, нечетких правил и исключения интерпретаций. Как известно, системы нечеткой логики включает в себя четыре основных этапа: фаззификации, базы правил,механизма вывода и нечеткой логики. Что показано на рисунке 1.
Фаззификация и дефаззификация этапы необходимых для преобразования и повторного преобразования реальных сигналов в нечеткие значения и наоборот.
Механизм вывода определяет степень соответствия текущей нечеткой входной информации к каждому правилу и решает, какие правила должны быть исключены в соответствии с полем ввода. Далее отобранные правила объединяются для формирования управляющих воздействий [2].
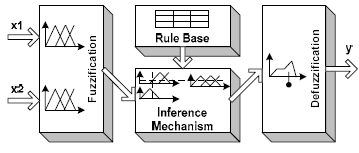
Рисунок 1 – Структура системы нечеткой логики
Нечеткого управления на основе нечеткой логики принятия решений вносит в приходим к управляющих воздействий. Нечетких контроллер использует пару значений ошибки и изменения ошибки и вычисляет управляющего сигнала, как показано на рисунке 2 [3].
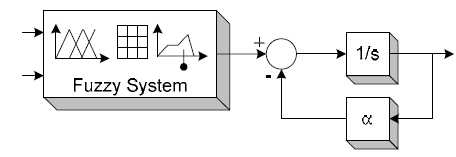
Рисунок 2 – Блок-схема нечеткой управляемой системы
Физические системы, как правило, динамичны. Таким образом, новый подход называется динамической нечеткой логикой систем для динамических задач систем управления. Динамически нечеткие логики систем состоят из статической нечеткой системы и динамический элементов с положительной обратной связью, что показано на рисунке 3. Динамические системы с нечеткой логикой первоначально исследованы Ли и Вуковичеи [4]. Мирти [4] предложил расширить динамических системы нечеткой логики на основании косвенного стабильного адаптивного управления нелинейными системами.
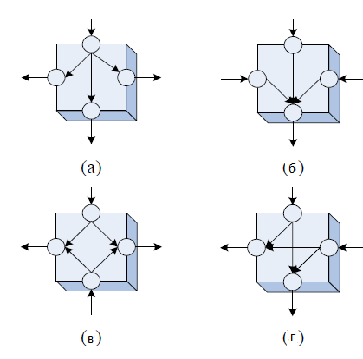
Рисунок 3 – Динамические системы с нечеткой логикой
Эти результаты сделали дистанционное обучение достойным дополнением и альтернативой традиционной формы, для многих преподавателей. Тем не менее, преподаватели также сообщили некоторые потенциальные препятствия, возникающие в процессе дистанционного обучения. Наиболее часто упоминаемые проблемы – это широко распространенное мнение об увеличении рабочей нагрузки и обеспокоенность тем, что данный вид обучения потребует больших затрат рабочего времени, и также то, что учреждениями более высоко ценится, в частности, исследования и публикации. За редкими исключениями [например, 6], в литературе сообщается, что дистанционное обучение требует больше времени, чем интенсивное аудиторное обучение [7, 2, 8, 3, 4]. Такое восприятие, как сообщается, является основным сдерживающим фактором для участия преподавателей в процессе дистанционного обучения, т.к. они могут отказаться от него; в то же время возрастает количество тех, у кого нет выбора или, кто хочет учиться на расстоянии даже с учетом предполагаемых повышенных требований [9, 10, 11].
Искусственные нейронные сети были успешно применены многих технических задач [5]. Существуют различные структуры искусственных нейронных сетей как многослойные, рецидивирующие, и сети Кохонена [6]. Блоки на основе нейронной сети, как различные структуры для практических целей, предложенны в [7]. Блок на основе нейронных сетей может достичь одновременной оптимизации структуры сети и подключения весов с использованием генетических алгоритмов [7].
Структура блока на основе нейронной сети позволяет прохождение сигнала в прямом и обратном направлениях. Каждый основной блок, которые имеют разные потоки сигнала соответствует простой нейронной сети прямого распространения. На рисунке 4 показаны основные блоки, которые имеют четыре различные типы внутренних Конфигураций [7].
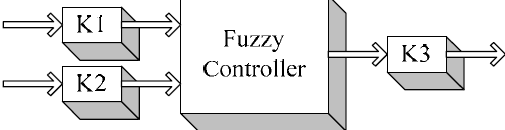
Рисунок 4 – Внутренние типы конфигурации фундаментальных блоков для блока на основе нейронных сетей
В закрытых системах управления с обратной связью, с использование опорного сигналы и / или измерительного сигнала в качестве входов нечеткого логического контроллера может вызвать некоторые неудобства. Есть некоторые исследования, для устранения помех, описанные в литературе [8-9]. В этих исследованиях, нечеткие множества типа 1 и типа 2 были использованы на выходе системы нечеткой логики. Но эти исследования являются статическими решениями для задач управления.
Как известно, системы управления, как правило, динамические. Динамические системы с нечеткой логикой можно использовать для управления динамическими системами. Первая научно-исследовательских работа о динамической системе с нечеткой логикой было изучена Ли и Вуковичем. Одно из этих исследований заключается в специальном предложении по идентификации и управления нелинейными системами с использованием динамических систем нечеткой логики [4]. Есть некоторая неопределенность и шумы в системах управления. Эти неопределенности и шумы важны для входов систем нечеткой логики. Основным критерием систем управления является разница между базовыми и измеряемыми значениями, как показано на рисунке 2. Поэтому устранение неопределенности и шумы очень важно для задачи управления.
Масштабируемые коэффициенты играют важную роль для конструкций нечетких логических контроллеров для получения хорошего поведения у переходных и установившихся областях. Эти масштабирования факторов могут быть постоянным или переменным. Как показано на рисунке 5.
Существуют три масштабируемых коэффициентов (K1, K2 и K3) для нечеткого логического контроллера. Настройка коэффициентов масштабирования в нечетких контроллеров изучалась многими исследователями в литературе [10-12].

Рисунок 5 – Коэффициенты масштабирования для нечеткого регулятора
Преимущества динамической системы с нечеткой логикой основанной на блоках нейронных сети могут быть объединены для получения более эффективной системы управления. На рисунке 6 показана блок - схема работы предлагаемого алгоритма в этом исследовании. Как показано на рисунок 6, блок на основе структуры нейронной сети использует входы для динамической системы нечеткой логики. Таким образом, блока на основе нейронной сети устраняет неопределенность и некоторые шумы, и обеспечивает задачу масштабирования входов.
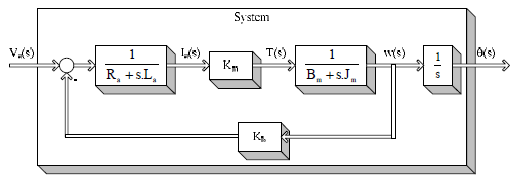
Рисунок 6 – Блок-схема предложенного алгоритма
Чтобы продемонстрировать эффективность предложенного алгоритма с позиции задачи управления был выбран двигатель постоянного тока.
Выбиранная система управления для моделирования блока на основе нейронной сети может быть использована для всех входов систем нечеткой логики для устранения шумов и обеспечения масштабирования. Предложенный алгоритм очень простой и эффективный.
Динамических нечеткой контроллер используется для управления положением двигателя постоянного тока. При моделировании, позиция 360 ° нормирована к 1. Система моделируется с фиксированным интервалом времени T = 0,0002 сек.
Предложенные алгоритмы были исследованы с помощью Моделирование в MATLAB / Simulink. Переданная функция двигателя постоянного тока системой позиционирования может быть определена в уравнении (1) для анализа поведения динамическим нечетким контроллером с блоком на основе нейронной сети.
Блок-схема двигателя постоянного тока показана на рисунке 7.

Рисунок 7 – Блок-схема якоря двигателя постоянного тока контролируемого
Функции принадлежности и таблица правил динамического нечеткого логического контроллера приведены на рисунке 8. Где (а -б)показаны функции принадлежности для входов, а (б) показаны функции принадлежности для выводов динамического нечеткого регулятора. Имеют вид пяти треугольных функций принадлежности. Треугольный вид выдран для простоты. Алгоритм Макси-минного вывода выбран для завершения нечеткой процедуры и выхода блока нечеткой логик контроллера, полученного методом центра тяжести в нечеткой логике.

Рисунок 8 – Функций принадлежности и базы правил динамической системы нечеткой логики
На рисунке 9 показаны результаты моделирования для позиции 1 (PU), посланной в двигатель постоянного тока. Как показано на этом графике, динамический нечеткий регулятор с блоком на основе нейронных сетей дает лучшие результаты, чем обычные нечеткий контроллер. На рисунке 10 показаны результаты моделирования с 5% шумом на исходную позицию. Динамического нечеткого регулятора с блоком на основе нейронной сети обеспечивает плавный выход системы в соответствии с обычным нечетким контроллером.
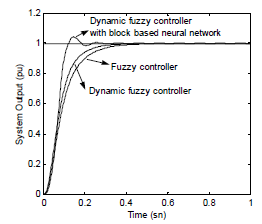
Рисунок 9 – Выходной ответ системы для исходного положения 1 PU
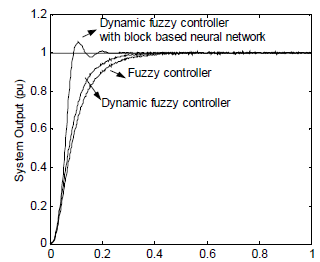
Рисунок 10 – Результаты моделирования с 5% шума для исходного положения 1 (PU)
В
этой статье представлена нечеткая динамическая структура управления с блоком на
основе нейронной сети. Предложенный алгоритм использует блок на основе
нейронной сети и устраняет некоторые нарушения и решает задачу масштабирования
входов динамической системы нечеткой логики. Предложенный алгоритм был успешно
проверен на управлении положением двигателя постоянного тока.
1. Karray F.O., De Silva C., Soft Computing and Intelligent Systems Design: Theory, Tools and Applications, Pearson Addison Wesley, England, 2004.
2. Driankov D., Hellendoorn H. and Reinfrank M., An Introduction to Fuzzy Control, Springer-Verlag Berlin Heidelberg, 1996.
3. Reznik L., Fuzzy Controllers, Newness, England, 1997.
4. Murthy O.V.R., Bhatt R.K.P., Ahmad N., Extended Dynamic Fuzzy Logic System (DFLS) Based Indirect Stable Adaptive Control of Nonlinear Systems, Elsevier, Applied Soft Computing, 4, 109-119, 2004.
5. Fausett L., Fundamentals of Neural Networks, Prentice Hall New Jersey USA, 1994.
6. Jang J.S. R., Sun C.T., Mizutani E., Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence, Prentice Hall, 1997.
7. Moon S.W., Kong S.G., Block Based Neural Networks, IEEE Trans. on Neural Networks, vol. 12, no. 2, pp. 307-317, 2001.
8. Foulloy L., Galichet S., Fuzzy Control with Fuzzy Inputs, IEEE Transactions On Fuzzy Systems, vol. 11, no. 4, pp. 437-448, August 2003.
9. Karakцse M., Ak?n E., Tip-1 Bulan?k Sistemlerde Tip-2 Bulan?k Girisler, ELECO’2004, s. 371-375, Bursa, 2004.
10. Yeh Z., A Systematic Method for Design of Multivariable Fuzzy Logic Control Systems, IEEE Transactions on Fuzzy Systems, vol. 7, no. 6, pp. 741-752, 1999. 11. Seng T.L., Khalid M., Yusof R., Tuning of a Neuro-Fuzzy Controller by Genetic Algorithm, IEEE Transactions on Systems, Man and Cybernetics, April, 1999.
12.
Duman E., Karakцse M., Ak?n E., A New Fuzzy Integral Model for Control
Systems: Adaptive Fuzzy Integral , TAINN’2003, Зanakkale,
Turkey, 2003.