На сайте приведена краткая версия перевода. Скачать полную версию

Декомпозиция

С проблемой декомпозиции контура часто встречаются при разработке БИС, например, при компоновке схемы, монтаже и моделировании. Объектами, предназначенными для декомпозиции при разработке БИС являются типично логические схемы или экземпляры стандартных элементов. Целью является разделение клеток на два или более блоков таким образом, чтобы количество взаимосвязей между блоками было сведено к минимуму. Сбалансированное ограничение микросхемы часто устанавливается изначально, что гарантирует примерно одинаковое содержание блоками количества компонентов.

Алгоритмы с минимальным числом пересечений выполняют декомпозицию неоднократно, пытаясь найти размещение, которое свело бы к минимуму маршрутизацию. После того, как схема декомпозирована в два блока, каждый блок разделяется на два подблока, и так далее, до тех пор, пока каждый бок не будет содержать одну или минимальное количество клеток. На этой стадии, каждому блоку может быть присвоено место в схеме. Сведя к минимуму количество взаимодействий между блоками на каждом этапе, алгоритм (минимизации загруженности) сечений способен свести к минимуму количество цепей соединений, которые должны быть маршрутизированы на длинные расстояния. Важным критерием является баланс в размещении алгоритмов, поскольку клетки должны быть равномерно распределены в схеме.

Данная глава исследует проблему декомпозиции и, в частности, использование генетических алгоритмов (ГА) для цепи декомпозиции. Мы начнем с формального описания задачи и краткого обзора алгоритмов декомпозиции. Применение стационарных ГА для декомпозиции контура описано ниже, и представлены результаты эксперимента. Глава завершается описанием гибридного ГА, представляющего локальную оптимизацию в дополнение к генетическому исследованию для того чтобы уменьшить время исполнения.

2.1 Описание задачи.

Задача декомпозиции цепи формально может быть представлена в графической теоретической записи в качестве взвешенного графа, с компонентами, представленными как узлы, и проводники, соединяющие их, в виде ребер. Вес узлов представляет размер соответствующих компонентов, а вес ребер представляет количество проводников, связывающих компоненты.

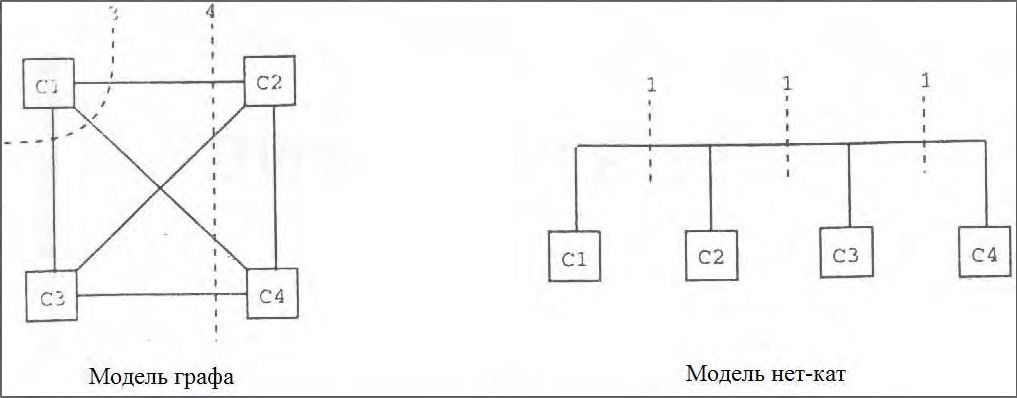
Рис.2.1 Сравнение моделей неткак и граф для декомпозиции

В своем общем виде, проблема декомпозиции заключается в разделении узлах графа, на два или нескольких непересекающихся подмножеств таким образом, чтобы сумма веса узлов, в каждом подмножестве не превышала заданной мощности, и сумма весов ребер связующих узлы в различных подмножествах была сведена к минимуму.

Швайкерт и Керниган проиллюстрировали недостаток использования простых граф-моделей для цепи декомпозиции. Они предложили модель неткат схемы, в которой единичная цепь представляет связь всеми компонентами, соединенными одной и той же сигнальной линией. Рассмотрим сеть из четырех компонентов, показанных на рис.2.1. Если схема смоделирована как граф с ребром для каждой связанной пары компонентов, она станет полностью связанным графом из четырех вершин. В случае, если данный граф будет декомпозирован, стоимость сечений будет трех или четырех реберной. Однако, если данная схема была представлена моделью неткат, в таком случае стоимость схемы станет только в одну сетку. По этой причине, БИС схемы обычно представляются в виде двудольного графа, состоящего из двух комплектов узлов (вершин), клеток и сеток.

2.1.2 Систематика алгоритмов декомпозиции

С 1970 года, когда Кэрриган и Лин предложили простое, основанное на графе эвристическое правило, что многократно улучшает первоначальную декомпозицию, используя технику поиска полустремящегося графа, было применено огромное количество техник комбинаторной оптимизации для решения проблем декомпозиции графа и цепи. В широком смысле, данные алгоритмы декомпозиции можно классифицировать в группы, согласно применявшейся стратегии оптимизации. Некоторые алгоритмы начинают с пустых комплектов и строят сегмент, добавляя один за раз. Это конструктивные алгоритмы. Другие начинают с произвольного изначального сегмента и непрерывно модифицируют его. Это так называемые, алгоритмы многократного улучшения. Данное является широкой классификацией алгоритмов.

Кластерные алгоритмы: Данные конструктивные алгоритмы [118] концентрируют данный комплект узлов в небольшие группы. Каждая группа должна удовлетворять различным критериям, как например, общему размеру и количеству внешних соединений. Для формирования кластера, выбирается кодовый узел для определения группы, и узлы к нему постоянно добавляются. Если размер или критерии внешних соединений нарушаются добавлением большего количества узлов, рост группы прекращается. Это известно под названием последовательного алгоритма, поскольку группа растет вокруг единичного кодового узла. Данный “поглощающий” подход прост и быстро работает, однако качество результатов, которые он производит, очень посредственные, поскольку конечный сегмент часто состоит из несвязанных узлов вокруг различных групп. Отчасти лучшие результаты можно получить путем одновременного построения различных групп вокруг большого количества кодовых узлов [118]. Данный параллельный подход стремится построить сегменты более похожим способом и широко применялся в прошлом для конструктивного построения изначальных сегментов, которые в дальнейшем улучшались посредством многократного алгоритма. Качество такого сегмента, однако, в конструктивной технике, сильно зависти от начального выбора узлов, и, разнообразный выбор может дать совершенно другой сегмент.

Граф алгоритмы: Данные алгоритмы разрабатываются в рамках операций на вершинах и ребрах графа, представляющего цепь, и обычно включают сегмент с двумя подмножествами. Кэрриган и Лин [114] и Bell Telephone Laboratory представили первый алгоритм многократного улучшения для графов декомпозиции.

Алгоритм К-Л начинается с произвольного сегмента и пытается минимизировать стоимость среза, производя незначительные локальные изменения по всем взаимозаменяемым парам узлов. Алгоритм делает несколько проходов. Каждый проход состоит из цепочки взаимозаменяемых пар узлов. Узлы являются взаимозаменяемыми в последовательности максимального усиления (прироста) стоимости срезов. В конце прохода все узлы становятся взаимозаменяемыми и стоимость срезов становится такой же, что и в начале прохода. Промежуточные сегменты проверяются и, сегмент с последовательностью парных обменов, который принимает наименьшее значение стоимости среза, возвращается в качестве выхода прохода. Из эмпирических наблюдений было обнаружено, что требуется только постоянное число проходов (типично в пределах два и четыре) независимых от графа. Качество конечного сегмента часто в значительной степени зависит от изначального сегмента. Поэтому хорошей идеей стало провести эвристически обоснованный алгоритм, такой как алгоритм К-Л, несколько раз со случайно сгенерированными начальными сегментами и найти лучшее решение, а также стандартные отклонения распределения.

Хотя алгоритм Ф-М быстр, он стремится сойти к локальному минимуму, когда связи появляются между многими клетками в списке прироста, и связи неотчетливо обрываются случайным способом, не давая дальнейшего решения последующего эффекта на другой сети, когда клетка выбрана для переноса.

Кришманутри уточнил способ выбора наилучших клеток для перенесения в другой блок, добавив механизм предварительного просмотра (МПП) [125]. Алгоритм Кришманурти поддерживает многомерную версию структуры данных Ф-М, перечни которого ожидали прирост клеток в будущих перемещениях. Таким образом, в случае связи текущих уровней прирост в срезе размера благодаря перемещению, алгоритм МПП Кришманурти выбирает клетку, которая дает лучший прирост в будущем перемещении. Поскольку исчисление и обновление многоуровневого прироста занимает значительное количество времени, типично 2-(называемый МПП2 ) или 3-(называемый МПП3) список уровня прироста используется на практике. Хотя временные непроизводительные издержки из 20 проходов уровня МПП3 сравнимо со 100 проходами алгоритма Ф-М, статистически наблюдается, что МПП3 дает приблизительно 7% улучшения размера среза по сравнению с алгоритмом Ф-М.

Было выяснено, что 100 проходов алгоритма Ф-М занимают практически тоже самое количество времени, что и 40 проходов алгоритма МПП2 и 20 проходов алгоритма ПВВП. В рамках качества результата, все три алгоритма были протестированы на большом количестве экспериментальных схем. Общее число наилучших комплектов среза, полученное данными тремя алгоритмами, запущенными как указывалось выше, равняется 1776 (Ф-М), 1898 (МПП2) и 1380 (ВППВ). Таким образом (ВППВ) было достигнуто улучшение в 27,3% в сравнении с МПП2, и в 22,3% в сравнении с Ф-М. Стало очевидным, что хотя МПП3 требует в сравнении с ВППВ в два раза больше времени, он оказался по результативности ниже ВППВ, что вызвало улучшение в сравнении с МПП3 на 16,6%.

Санчис [200] модифицировала алгоритм Кришнамурти, чтобы провести многоканальную декомпозицию. Она разработала структуру данных для представления многоканальной декомпозиции различных блоков, и экспериментальным образом, доказала, что оптимальное число уровней прироста зависит от количества блоков, размера сети и степени распределения сегмента сети, а не от размера сети.

Коэффициент среза: Несмотря на то, что граф алгоритмы очень успешны в последовательном делении на две части и многоканальном делении, у них есть одно ограничение в том, что они не включают тот факт, что реальные цифровые сегменты являются иерархическими по природе. Присутствие иерархии налагает определенное количество кластеризации. Граф алгоритмы очевидны из этих кластеров и стремятся разделить граф путем строго сбалансированной (или без границ приемлемого дисбаланса) декомпозиции, и зачастую получившиеся размеры срезов далеки от минимальных. Цель алгоритма коэффициента среза первоначально представлена Wei и Cheng [235], заключается в том, чтобы определить естественные кластеры в сегменте и уберечь их от усечения комплектом среза и, таким образом, алгоритм фокусируется поиске наилучшего коэффициента среза, в противовес минимальному размеру среза. Коэффициент среза благодаря делению графа на два блока, дан в соотношении комплекта среза между двумя блоками и продуктом мощности (размером) каждого блока. Хотя знаменатель является максимальным, когда оба блока одинакового размера, благодаря природе кластеризации, минимальный коэффициент среза можно получить для особого комплекта среза, который может разделить их на два неравных по величине блока. Цель алгоритма коэффициента среза - эвристически найти наилучший коэффициент среза, вместо поиска минимального размера среза. Данный подход применялся для установки списка соединений экспериментальных схем, и как оказалось, размер среза может быть улучшен до 70% в сравнении с теми, что получены алгоритмом Ф-М.

Стохастические алгоритмы: Среди разнообразных и хорошо известных методов случайной организации, алгоритм смоделированного закаления широко применяется для решения разнообразных оптимизационных решений БИС разбивок[115]. Алгоритм начинается со случайного решения и производит пошаговую очистку путем перемещения клеток из их текущего положения в новые места с тем, чтобы сформировать новое решение. Как правило, все перемещения, уменьшающие стоимость, принимаются, а перемещения, увеличивающие стоимость, также принимаются, согласно функции вероятного решения. Такое решение производится сравнением рационального числа, выбранного случайно. Между 0 и 1 функцией продолжительной вероятности, ценность которой уменьшается согласно заранее установленной шкале охлаждения и магнитуды изменений стоимости, подобной молекулярному распределению Максуэлла-Больцмана. Таким образом, когда алгоритм начинается, внутренняя высокая температура установки позволяет многочисленные перемещения, которые в действительности значительно увеличивают стоимость от текущей ценности. Впоследствии, когда температура достигает окончательного значения, доступно только очень малое количество перемещений, увеличивающих стоимость. Таким образом, моделированное закаление ведет себя как стабильный алгоритм, способный найти всеобъемлющее оптимальное решение. Главная проблема моделированного закаления заключается в том, что оно занимает значительно большее количество времени, чем алгоритм линейного времени, такой как алгоритм Ф-М.

Для того чтобы уменьшить временную сложность смоделированного на основе закаления алгоритма сегментированной декомпозиции, Грин и Саповит [87] разработали новый безотказный метод, который не отрицает ни одно перемещение. Они отобрали перемещения путем прикрепления весовых факторов к ним, в зависимости от их влияния на стоимость действия. Данная технология работает чрезвычайно хорошо для декомпозиции сегмента на небольшое количество кластеров, в особенности, если средняя степень узлов невелика. Скорость прохода таких безотказных смоделированных закаленных алгоритмов линейная.

Невральные алгоритмы: Йи и Мазумдер [243] представили невральную сетевую модель цепи декомпозиции, используя технологии многократного улучшения. В их презентации комплект компонентных нейронов описывает, какие клетки находятся в каких блоках сегмента, в зависимости от того, является ли компонентный нейрон в состоянии запуска (1) или нет(0). Для того, чтобы представить сети с компонентными нейронами k (то есть, сети, которые полностью находятся в одном блоке, или сети, которые имеют ровно одну клетку в одном блоке, а остальные – в других), комплект некомпонентных нейронов k, связанных с компонентными нейронами, с фиксированными позитивными синоптическими весами были аккуратно добавлены таким образом, что невральная сеть попытается обработать критические сети соответствующим образом. Невральная сеть была спроектирована так, что она должна удовлетворить установленные критерии, и работа невральной сети была протестирована несколькими экспериментальными схемами списка соединений и сравнена с результатами алгоритма Ф-М. Для всех цепей экспериментальных схем получено распределение размеров среза для 300 произвольных внутренних сегментов для невральной сети и подсчитаны для алгоритма Ф-М. Ключевое преимущество технологии невральной сети заключается в достижении гигантского ускорения над ПО алгоритмами.

2.2 Контурная декомпозиция генетическим алгоритмом (ГА).

После краткого обзора генетического алгоритма, который был разработан для решения задачи декомпозиции схемы, будут обсуждены детали всех генетических операций. В сущности, данная версия ГА может быть описана как статический ГА [50], с мутацией смодулированного закаления популяции.

ГА начинается с нескольких альтернативных решений проблемы оптимизации, что рассматривается как индивиды в популяции. Данные решения закодированы в виде двоичных цепочек, и называются хромосомами. Исходная популяция создана случайным способом. Данные индивиды оценены, при помощи функции проблемно-ориентированной пригодности. Пригодная ценность приведена к масштабу при помощи подходящей функции, sigma-масштабирования.

Затем ГА использует данные индивиды для производства новых поколений с ожидаемыми лучшими решениями. В каждом поколении, два из индивидов выбраны вероятностно в качестве “родителей”, с вероятностным выбором пропорциональным их пригодности. Таким образом, более подходящий индивид, ожидаемо содержащий некоторые полезные характеристики, имеет более высокую вероятность самостоятельного размножения. Скрещение происходит на этих двух индивидах для порождения двух новых индивидов, называемых-“потомками”, путем изменения частей их структуры.

Это позволяет ГА тщательно проверить различные характеристики в различных сочетаниях и увидеть, сохраняют ли все еще индивиды свою пригодность. Новые индивиды оцениваются и затем сравниваются с остальной популяцией. В случае, если они лучше худших индивидов, и если они не идентичны ни одному другому индивиду, в таком случае, они замещают собой худшие индивиды популяции.

Следующий шаг- мутация. Пошаговое изменение производится для каждого члена популяции, с небольшой долей вероятности. После того, как произведено мутирование на индивиде, он уже больше не имеет точной комбинации унаследованных им от двух родителей, характеристик, но также содержит в себе это дополнительное изменение, произведенное в процессе мутации. Это обеспечивает, то, что ГА может проанализировать новые характеристики, которые еще могут отсутствовать у популяции. Это делает все исследуемое пространство достижимым, несмотря на конечность размера популяции. Изменение пригодности благодаря данной мутации оценивается. Если пригодность увеличилась, мутация всегда принимается, а если пригодность уменьшилась, тогда мутация принимается вероятностно, основываясь на степени уменьшения пригодности. Это защищает популяцию от инертности в течение долгого времени когда большая часть потомков, произведенных скрещением, хуже, чем популяция и подвергается выбраковке.

Список сетевых соединений первичной обработки, и I/O площадки обработка: Во-первых, список входа модифицирован для того, чтобы ускорить алгоритм и улучшить его работу. Далее список преобразовывается в новый список, на котором работает ГА. Список команд предварительной обработке идентичен как для алгоритма последовательного деления на две части, так и для многоканального алгоритма. Сети одиночного выхода удалены из списка. Сети одиночного выхода могут явиться результатом неподключенных выходов стандартных клеток, которым назначены холостые названия сетей.

Данный алгоритм был протестирован при помощи стандартных клеточных тестах MCNC, которые включают I/O площадки. Когда I/O площадке задаются фиксированные координаты, они устанавливаются постоянно для сегментов вдоль границ чипов, основанных на этих координатах, как при последовательной, так и при многоканальной декомпозиции. I/O площадки не требуют установки к хромосомам, поскольку их сегменты уже известны. Однако они учитываются при оценочной функции среза сети.

Представление хромосом: Каждая клетка представлена 1 битом в хромосоме, ценность которой определяется сегментом, к которому клетка приписана. Хромосома хранится в матрице 32-х битных упаковочных двоичных форматов слов, с некоторыми из нечитаемых битов в последнем двоичном слове. Список сетей проходит в порядок поиска в ширину, и клетки приписываются к хромосоме в таком порядке. Таким образом, две клетки напрямую связаны друг с другом, существует высокая вероятность, что их сегментные биты будут близки друг к другу в хромосоме.

Преимущество данного метода заключается в том, что кластеры клеток имеют высокую вероятность формирования подобных кластеров битов в хромосоме. При скрещении, такие близко расположенные кластеры битов имеют высокую вероятность получения их сегментных назначений от одного из “родителей” в качестве группы, и таким образом, остаются нетронутыми. Это в значительной степени улучшает поиск ГА и делает оператора инверсии ненужным для данной операции.

Оценка: Оценка среза сети использует операцию шаблонирования битов. Для каждой сети, многословный шаблон размером с хромосому предварительно подсчитывается, таким образом, чтобы клетка была подключена к сети, и устанавливается соответствующая бит-позиция.

Оценка баланса сегмента производится подсчетом числа таковых в хромосоме. Это может быть сделано 8 бит за раз одновременно, используя таблицу побитового просмотра.

2.2.1 Ассимиляция и резервная проверка:

Два новых “потомка”, сформированные в каждом воспроизведении, ассимилируются в популяцию только если они лучше, чем наихудшие индивиды существующей популяции.

Мутированная версия заменяет немутированную того же самого индивида популяции. Обратите внимание, что она не заменяет другую, менее пригодную версию; иначе, популяция будет содержать обе мутированные и немутированные версии того же самого индивида. Они практически идентичны друг другу и станут причиной преждевременной конвергенции.

Линейная и эквивалентная функции используются как приближение к показательной функции в смоделированном замораживании. Это главным образом для скорости. Эквивалентная функция более точно подходит характеристикам показательной функции для большого увеличения стоимости: то есть, для очень большого увеличения стоимости, существует все еще небольшая, однако, конечная вероятность приемлемости. Однако, она меньшей практической ценности, поскольку в небольших мутациях, стоимость, к сожалению, изменяется в большом количестве. Линейная функция, которая является наибыстрейшим приближением, обеспечивает адекватное выполнение и ничего не получается достичь используя эквивалентное приближение.

Данный метод мутации подобен небольшому количеству непрерывных поддерживающих постоянную температуру смоделированных замораживаний каждого члена популяции. Цель не в оптимизации индивидов, используя смоделированное замораживание: следовательно, температура не варьируется. Если индивиды были оптимизированы, (или в значительной степени изменены) использованием смоделированной заморозки, то информация, унаследованная «потомками» от «родителей» будет утеряна, и ГА не сможет выполнять свою функцию. Вот почему использовалась неочищенное приближение функции показательной вероятностной приемлемости, поскольку ее размер не критический для операции алгоритма.

Настоящая цель обеспечить небольшое постоянное возмущение в популяции, то есть такие небольшие в количестве, что их влияние чувствуется только в течение долгого периода стагнации в ГА. Когда популяция уже настолько хороша, что ГА непрерывно генерирует “потомков”, которые отклоняются, тогда способ продвижения дальше будет возмутить слегка популяцию, до тех пор, пока некоторые “потомки“ не будут приняты, и ГА выйдет из под местного оптимума.

2.2.3 Генетическая многоканальная декомпозиция.

Представление хромосом: Сегмент, заданный для каждой клетки представляет многобитовый код, хранимый в качестве единичного слова удобного размера. Поскольку параллелизм не может быть использован в данном случае, упаковка кодов в бытовую строку не выполняется, чтобы сохранить время упаковки/распаковки на каждом шаге. Порядок поиска в ширину был применен чтобы задать клетки в хромосоме, как описано выше для алгоритма последовательного деления на две части.

Генетические операторы: Скрещение и мутация представлены традиционным способом. Хромосомы срезаются у границ слова, и левая часть одного из “родителей” сочетается с правой частью другого, чтобы воспроизвести “потомка”. Другой дополняющий “потомок” производится при помощи сочетания оставшейся части “родителей”. Это заставляет некоторые клетки унаследовать их распределение сегментов от одного из “родителей” и некоторые от другого. Получившийся “потомок” всегда легален, однако это может быть несбалансированная сегментация, со слишком большим количеством клеток в некоторых сегментах и слишком малым количеством в других. Баланс сегмента исправляется наказанием в функции пригодности.

Сигма масштабирование, ассимиляция и контроль дуплицирования такие же что и при алгоритме последовательного деления на две части.

Мутация происходит выбором случайного слова и изменением его до случайной ценности в сравнении с текущей ценностью, то есть, перемещение случайно выбранной клетки в новый случайный сегмент. Метод вероятностной приемлемости для мутации также тот же самый, что и для алгоритма для последовательного деления.

2.2.5 Результаты:

Программы последовательного разбиения на две части и многоканального последовательного разделения на две части были протестированы эталонным тестом списка сети MCNC стандартного размещения клеток. Рис 2.10 показывает работу алгоритма для различного оценивания параметров ГА. Таблица 2.1 показывает параметры ГА, примененные для остальных экспериментов. На рис 2.10 один параметр варьируется во времени. В то время как другие остаются фиксированными, как показано на Таблице 2.1.