Abstract
Content
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. An approach to the unification of synthesis of Moore FSM on FPGA
- Conclusion
- References
Introduction
Digital systems are widely used as basic elements of computer technologies, automatics, robotics, manufacturing, transport. Creation of very large-scale integration circuits (VLSI), building of systems-on-chip (SoC), development of field-programmable gate arrays (FPGAs) and complex programmable logic devices (CPLDs) changed the basis of implementation digital systems and proposed increased requirements to the process of their design, which has led to the widespread using of computer-aided design (CAD) tools and hardware description languages (HDLs). All this should raise quality of the resultant product, promote in realization of multifold analysis and testing. Besides, new base-oriented methods of combinational and sequential synthesis of logical circuits were created, the greatest effectiveness from which can be reached in the case of application automation and joint combined using with already known algorithms.
Model of Moore finite state machine (FSM, offered by E. Moore in 1956 and named in his honor), as synchronous sequential circuit, is the part of numerous digital systems and is used in construction of control devices. High complexity of integrated circuits (which is increasing, according to the G. Moore's law) and theoretical basis of automatic calculations make possible the implementation of comprehensive algorithms of processing information. However direct realization of algorithms can lead to inefficient using of crystal's resources and extension of project's cost.
1. Theme urgency
The number of methods of Moore FSM's hardware optimization is known: minimization of the amount of states (state reduction) and their specific encoding (state assignment), using features of target basis and algorithm of functioning, multilevel logic circuit's implementation. Mentioned methods are quite effective, but for getting the most economic FSM's implementation they have to be used jointly.
Master's work is dedicated to the actual scientific task of development a unified approach to the synthesis of Moore FSM, which is directing on hardware amount reduction in resultant device and is including algorithmic, combinatory and circuitry optimizing techniques. FPGAs by Xilinx, which combine functionality, programmability and availability to consumers, are used as the target basis. CAD Xilinx ISE, Verilog HDL and Java SE are applied as tools of the research.
2. Goal and tasks of the research
Development of an approach to the unification of synthesis Moore FSM, directing on hardware amount reduction in FPGA is the goal of research.
Main tasks of the research:
- Analysis methods of minimization amount of states in completely and incompletely specified Moore FSM.
- Estimation ways of hardware amount reduction with the help of encoding states of Moore FSM.
- Search and detection characteristics of existing construction methods of logic circuits of Moore FSM and estimation possibilities of their use on FPGA.
- Association of functionally different optimization directions of Moore FSM hardware amount into the unified approach to synthesis and formation recommendations for it's use.
- Design of alternative variants of basic stages of unified Moore FSM synthesis process and estimate of it's efficiency.
Research object: Moore FSM synthesis.
Research subject: association of hardware amount reduction methods at Moore FSM implementation on FPGA.
3. An approach to the unification of synthesis of Moore FSM on FPGA
An approach to the unification of synthesis of Moore FSM on FPGA is offered in article [1]. It joints several possibilities of optimization and is directed on FPGA (fig. 1). Entity of an approach consists in sequential application of algorithmic, combinatory and circuitry stages and using FPGA-oriented tools: CAD and HDLs.
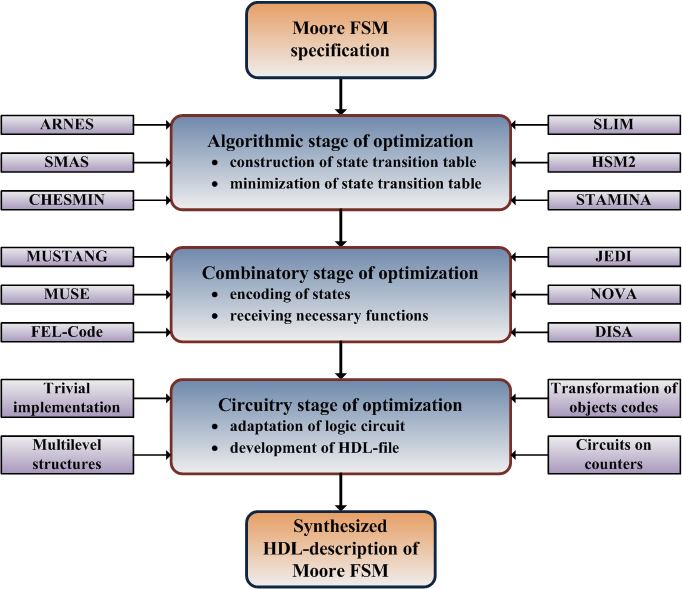
Figure 1 Ц An approach to the unification of synthesis of Moore FSM
On the first step of algorithmic stage of synthesis, arbitrary Moore FSM specification is led to a uniform type Ц state transition table. Necessity of leading to a uniform type is caused by possibility of specification Moore FSM with the help of different representation forms, such as: graph schemes of algorithm, state diagrams, ASM-diagrams (ASM Ц Algorithmic State Machine) [2-4]. Second step of algorithmic stage consists of minimization of the state transition table. Algorithms of Brzozowski, ARNES, SMAS, CHESMIN, SLIM, HSM2, STAMINA, OPTIMIST, BICA, ISM can be used for this [3, 5-16].
Combinatory stage is directed on effective encoding of minimized transition table's states and, also, on receiving of hardware-minimum functions of the next state and, at necessity, of output functions of FSM. Considerable influence of states encoding method on parameters of resultant logical circuit caused development of various approaches, directed on decreasing of power expenses, high-speed performance, minimization of hardware amount. The last one of these approaches can be used on combinatory stage of synthesis with the help of application, adaptation and modification of MUSTANG, MUSE, FEL-Code, JEDI, NOVA, Two-Hot Encoding, DISA, one-hot and positional-binary states encoding algorithms [17-37].
Circuitry stage of synthesis process assumes using Moore FSM logical circuit's construction methods, directing on reduction of hardware amount of target chip. Trivial and multilevel implementations, structures with transformation of objects codes, circuits on counters can be carried to these methods [37]. Modern digital design is oriented on using HDLs (basically, VHDL and Verilog), because of what the second step of circuitry stage is development of HDL program, which describes Moore FSM and is suitable for processing of appropriate CAD and immersion into the chip.
The described unified synthesis process can be successfully implemented automatically and assume only user's administrative functions: describing of Moore FSM and choosing algorithms and structures, which should be used. Moreover, presented approach can be applied to the number of other modern basis (CPLD, ASIC) and define the general direction of optimizing works at synthesis of logic sequential circuits.
Five Verilog-programs, describing given Moore FSM [38] (fig. 2) in various ways, were designed for an estimation of unified synthesis process application to the exact example:

Figure 2 Ц State diagram of Moore FSM
(animation: 10 frames, 5 cycles of repeating, 160 kilobytes)
(xi Ц input signals, yi Ц bites of state code, zi Ц output signals)
- Implementation of not minimized Moore FSM with the help of XST (Xilinx Synthesis Technology) analyzer [39] (experiment 1).
- Implementation of minimized Moore FSM with the help of XST (Xilinx Synthesis Technology) analyzer (experiment 2).
- Implementation of minimized Moore FSM on twoЦlevel circuit [40] with positional-binary states encoding. Use of ROM with asynchronous reading [39] (experiment 3).
- Implementation of minimized Moore FSM on twoЦlevel circuit with positional-binary states encoding. Use of ROM with synchronous reading [39] and an additional signal of synchronization (experiment 4).
- Implementation of minimized Moore FSM on twoЦlevel circuit with positional-binary states encoding. Use of ROM with synchronous reading and back front of the main signal of synchronization (experiment 5).
All researches were held with the help of CAD Xilinx ISE 13.1 for the family of FPGA Xilinx Spartan-3, namely for the chip XC3S200. Results for cumulative hardware amount for five variants of implementation are graphically shown on fig. 3.

Figure 3 Ц Results of experiments
If the goal of optimization is amount of LUT-cells, the best result has been received at use of twoЦlevel implementation of minimized Moore FSM with synchronous ROM and two signals of synchronization (experiment 4). In comparison with experiment 1, number of slices has decreased in 3 times, number of flip-flops Ц in 1,5 times, number of LUT-cells Ц in 2,5 times. However in this case has increased the total of circuit's outputs, number of synchronization signals and one RAM (Random Access Memory) module has been involved.
Conclusion
Qualitative synthesis of digital systems, and Moore automata in particular, is one of the areas of logic design,
and is not only theoretical research but also of practical interest. Development of optimal digital devices opens the way for
more efficient use of capacity basis the implementation of compaction
of projects, reduce material costs.
Master's work is devoted to actual scientific problem of combining the basic methods of minimizing the instrumental Moore automata. In the trials carried out:
- The structure of a unified process for the synthesis of Moore automata and defines the functions of its components.
- Based on analysis of the literature highlights the main algorithms that can be used in the proposed approach to the unification of the synthesis of Moore automata.
- A number of experiments on the use of a unified process for the synthesis of Moore automata, analyzed the results.
- The possibilities of integrated automation of the developed approach to the unification of the synthesis of Moore automata are estimated requirements for the software by searching for functionally similar software synthesis of sequential logic circuits.
Further studies focused on the following aspects:
- Qualitative improvement of the proposed approach to the unification of the synthesis of Moore automata, its complement and expand.
- Delimitation of the effectiveness of different variants of the basic stages of a unified process for the synthesis of Moore automata.
- Adaptation of known methods of constructing the logic of Moore automata to the base FPGA.
- Develop cross-platform functionality and computer-aided design of Moore automata (CAD) software that implements the proposed unified process synthesis.
This master's work is not completed yet. Final completion: December 2011. The full text of the work and materials on the topic can be obtained from the author or his head after this date.
References
- овалев —.ј. ѕодход к унификации процесса синтеза ћѕј ћура дл€ FPGA / —.ј. овалев, ».я. «еленЄва, ≈.–. “атолов // ћатериалы ƒвенадцатого международного научно-практического семинара «ѕрактика и перспективы развити€ партнерства в сфере высшей школы». Ц ƒонецк-“аганрог, 2011. Ц “ом 2. Ц —. 45-48.
- Mano M. Digital design / M. Mano. Ц Prentice Hall, 2003. Ц 516 pp.
- Nelson V. Digital logic circuit analysis and design / V. Nelson, H. Nagle, J. Irwin, B. Carroll. Ц Prentice Hall, 1995. Ц 842 pp.
- Barkalov A.A. Synthesis of operational and control automata / A.A. Barkalov, L.A. Titarenko. Ц Donetsk: DonNTU, TechPark DonNTU UNITECH, 2009. Ц 256 pp.
- Avedillo M.J. New approach to the state reduction in incompletely specified sequential machines / M.J. Avedillo, J.M. Quintana, J.L. Huertas // Proceedings of IEEE International Symposium on Circuits and Systems. Ц New Orleans, 1990. Ц pp. 440-443.
- Avedillo M.J. SMAS: a program for the concurrent state reduction and state assignment of finite state machines / M.J. Avedillo, J.M. Quintana, J.L. Huertas // Proceedings of IEEE International Symposium on Circuits and Systems. Ц 1991. Ц vol. 3. Ц pp. 1781-1784.
- Champarnaud J.-M. Split and minimizing: Brzozowski's algorithm / J.-M. Champarnaud, A. Khorsi, T. Paranthoen // Prague Stringology Conference. Ц Prague, 2002. Ц pp. 96-104.
- Goren S. CHESMIN: a heuristic for state reduction in incompletely specified finite state machines / S. Goren, F. Ferguson // Proceedings of the Conference on Design, Automation and Test in Europe. Ц 2002. Ц pp. 248-254.
- Higuchi H. A fast state reduction algorithm for incompletely specified finite state machines / H. Higuchi, Y. Matsunaga // 33rd Annual Conference of Design Automation. Ц Las Vegas, 1996. Ц pp. 463-466.
- Hu H. HSM2: a new heuristic state minimization algorithm for finite state machine / H. Hu, H.-X. Xue, J.-N. Bian // Journal of Computer Science and Technology. Ц 2004. Ц є 19 (5). Ц pp. 729-733.
- Rho J.-K. Exact and heuristic algorithms for the minimization of incompletely specified state machines / J.-K. Rho, G. Hachtel, F. Somenzi, R. Jacoby // IEEE Transactions on Computer-Aided Design. Ц 1994. Ц vol. 13. Ц pp. 167-177.
- Xu Y. Describing an n log n algorithm for minimizing states in deterministic finite automaton [Ёлектронный ресурс]. Ц –ежим доступа: http://www.cs.sun.ac.za....
- Fuhrer R.M. OPTIMIST: state minimization for optimal 2-level logic implementation / R.M. Fuhrer, S.M. Nowick // Proceedings of International Conference of Computer-Aided Design. Ц 1997. Ц pp. 308-315.
- Pena J.M. A new algorithm for exact reduction of incompletely specified finite state machines / J.M. Pena, A.L. Oliveira // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. Ц 1999. Ц vol. 18 (11). Ц pp. 1619-1632.
- Kam T. A fully implicit algorithm for exact state minimization / T. Kam, T. Villa, R. Brayton, A. Sangiovanni-Vincentelli // Proceedings of the Design Automation Conference. Ц 1994. Ц pp. 684-690.
- Almeida M. On the performance of automata minimization algorithms / M. Almeida, N. Moreira, R. Reis // Technical Report Series: DCC-2007-03. Ц 2007. Ц 12 pp.
- Slusarczyk A. State assignment techniques Ц short review [Ёлектронный ресурс]. Ц –ежим доступа: http://web.cecs.pdx.edu....
- De Micheli G. KISS: a program for optimal state assignment of finite state machines / G. De Micheli, R. Brayton, A. Sangiovanni-Vincentelli // Proceedings of IEEE International Conference of Computer-Aided Design. Ц Santa Clara, 1984. Ц pp. 209-211.
- De Micheli G. Optimal state assignment for finite state machines / G. De Micheli, R. Brayton, A. Sangiovanni-Vincentelli // IEEE Transactions on Computer-Aided Design. Ц 1985. Ц pp. 269-285.
- De Micheli G. Optimal encoding of control logic / G. De Micheli // Proceedings of the International Conference on Circuits and Computer Design. Ц 1984. Ц pp. 16-22.
- El-Maleh A. Finite state machine state assignment for area and power minimization / A. El-Maleh, S.M. Sait, F.N. Khan // Proceedings of IEEE International Symposium on Circuits and Systems. Ц 2006. Ц pp. 5303-5306.
- Devadas S. MUSTANG: state assignment of finite state machines targeting multilevel logic implementations / S. Devadas, H.-K. Ma, A.R. Newton, A. Sangiovanni-Vincentelli // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. Ц 1998. Ц vol. 7 (12). Ц pp. 1290-1300.
- Du X. MUSE: a multilevel symbolic encoding algorithm for state assignment / X. Du, G. Hachtel, B. Lin, A.R. Newton // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. Ц 1991. Ц vol. 10 (1). Ц pp. 28-38.
- Kubatova H. FEL-Code: FSM internal state encoding method / H. Kubatova, M. Becvar // Proceedings of 5th International Workshop on Boolean Problems. Ц Freiberg, 2002. Ц pp. 109-114.
- Lin B. Synthesis of multiple level logic from symbolic high-level description languages / B. Lin, A.R. Newton // Proceedings of the International Conference on VLSI. Ц Munich, 1989. Ц pp. 187-196.
- Villa T. NOVA: state assignment of finite-state machines for optimal two-level logic implementation / T. Villa, A. Sangiovanni-Vincentelli // IEEE Transactions on Computer-Aided Design. Ц 1990. Ц pp. 905-924.
- Gupta, B.N.V.M. A state assignment scheme targeting performance and area / B.N.V.M. Gupta, H. Narayanan, M.P. Desai // Proceedings of 12th International Conference on VLSI Design. Ц 1999. Ц pp. 378-383.
- Martinez M. A dynamic model for the state assignment problem / M. Martinez, M.J. Avedillo, J.M. Quintana, J.L. Huertas // Proceedings of Design, Automation and Test in Europe. Ц Paris, 1998. Ц pp. 835-839.
- Golson S. One-hot state machine design for FPGAs / S. Golson // Proceedings of the 3rd PLD Design Conference. Ц Santa Clara, 1993. Ц pp. 1-6.
- Almaini A. State assignment of finite state machines using a genetic algorithm / A. Almaini, J. Miller, P. Thomson, S. Billina // IEEE Proceedings on Computer and Digital Techniques. Ц 1995. Ц pp. 279-286.
- Amaral J. Designing genetic algorithms for the state assignment problem / J. Amaral, K. Turner, J. Chosh // IEEE Transactions on Systems, Man, and Cybernetics. Ц 1995. Ц vol. 25. Ц pp. 659-694.
- Chyzy M. Evolutionary algorithm for state assignment of finite state machines / M. Chyzy, W. Kosinski // Artificial Intelligence Methods. Ц Gliwice, 2003. Ц pp. 51-52.
- Nedjah N. Evolutionary synthesis of synchronous finite state machines / N. Nedjah, L.M. Mourelle // Evolvable Machines. Ц Berlin, 2004. Ц pp. 103-128.
- Chattopadhyay S. Area conscious state assignment with flip-flop and output polarity selection for finite state machine synthesis Ц a genetic algorithm approach / S. Chattopadhyay // The Computer Journal. Ц 2005. Ц vol. 48 (4). Ц pp. 443-450.
- Hasteer G. Parallel algorithms for state assignment of finite state machines. Master's thesis. Ц University of Illinois, 1996. Ц 58 pp.
- Bader D.A. A parallel state assignment algorithm for finite state machines / D.A. Bader, K. Madduri // Proceedings of IEEE Conference on High-Performance Computing. Ц Bangalore, 2004. Ц pp. 297-308.
- Ѕаркалов ј.ј. —интез микропрограммных автоматов на заказных и программируемых —Ѕ»— / ј.ј. Ѕаркалов, Ћ.ј. “итаренко. Ц ƒонецк: ƒонЌ“”, “ехнопарк ƒонЌ“” ”Ќ»“≈’, 2009. Ц 336 с.
- ”илкинсон Ѕ. ќсновы проектировани€ цифровых схем / Ѕ. ”илкинсон. Ц ћ.: »здательский дом
¬иль€мс
, 2004. Ц 320 с. - XST User Guide for Virtex-4, Virtex-5, Spartan-3, and Newer CPLD Devices [Ёлектронный ресурс]. Ц –ежим доступа: http://www.xilinx.com....
- Ѕаркалов ј.ј. —интез устройств управлени€ на программируемых логических устройствах / ј.ј. Ѕаркалов. Ц ƒонецк: ƒонЌ“”, 2002. Ц 262 с.
