ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Сучасна ринкова економіка належить до класу змішаних. У ній виробництво розвивається під впливом власних ринкових ефектів, викликають, найчастіше, не цілком логічно обгрунтовану споживчу активність домашніх господарств. При цьому держава регулює цей процес: встановлює правову структуру бізнесу і контролює її дотримання, спираючись на дані статистики виробництва і споживання, зазвичай має випадковий характер.

Макроекономічна модель такої економіки повинна являти собою складний апарат, зокрема враховує і різноманітні описи невизначеності ринкового і державного, внутрішнього і зовнішнього регулювання. Необхідно реалізувати математичну методологію, більш повно враховує "поведінкові" аспекти при описі процесів розвитку ринкової економіки в кризових і перехідних умовах.

Метою даної роботи є розвиток апарату макроекономічного моделювання з використанням нечітко-возможностних математичних методів аналізу мікроекономічних процесів.

Для реалізації поставленої мети необхідно виконати ряд завдань:

Об'єктом дослідження даної роботи є ринковий механізм встановлення загальної рівноваги в економічній системі на макро- і мезорівні.

Предмет дослідження - сучасний апарат моделювання процесів встановлення і підтримки загальної економічної рівноваги і можливості його застосування.

1. Основні проблеми підвищення адекватності моделей і методів макроекономічного моделювання

Викладаються основні проблеми розробки адекватних моделей ринкової економіки. Проводиться детальний аналіз методологічних і методичних аспектів проблеми аналізу макроекономічних взаємозв'язків. На основі розгляду особливостей сучасної методології макроекономічних досліджень викладені загальні поняття і дана класифікація макроекономічних моделей, розроблених до теперішнього часу [1].

Існує об'єктивна подвійність у використанні математиче-ських структур при макроекономічному моделюванні цілісної економічної системі (ЦЕС): з одного боку, як моделей для безлічі істинних формул, з іншого боку, як змістовно інтерпретується моделі реальної ЦЕС.

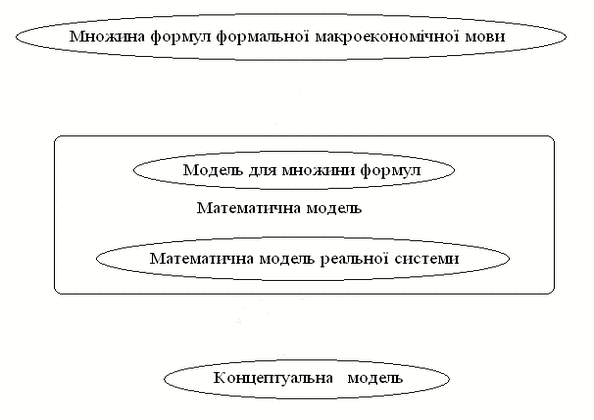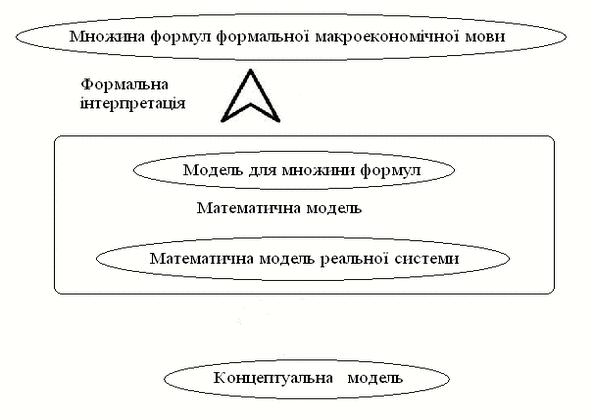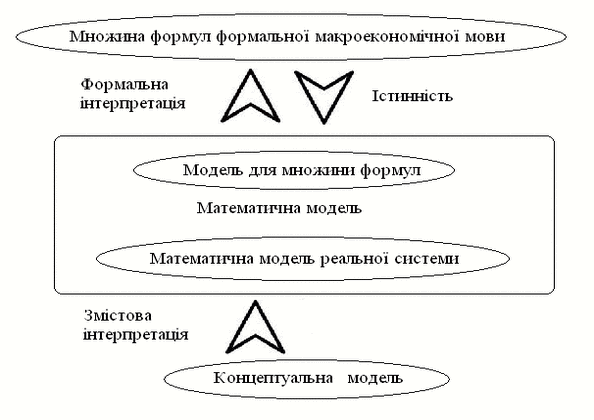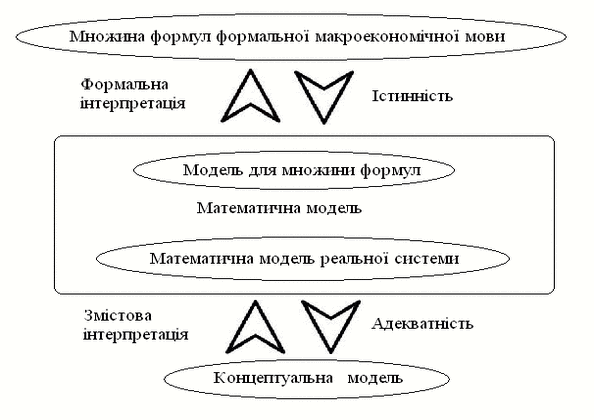
Математична інтерпретація подвійності макроекономічних моделей

Рисунок 1 – Математична інтерпретація подвійності макроекономічних моделей (анімація: 5 кадрів, 5 циклів повторення, 34,8 кілобайт)

Основним інструментом теоретичного вирішення даної подвійності виступає вимога адекватності моделі і реальної ЦЕС, а формалізованими методами забезпечують адекватність моделі і ЦЕС є методи декомпозиції і агрегування [2].

Існує два протилежні напрямки (школи) забезпечення вимоги адекватності макроекономічних моделей і ЦЕС: класичне і кейнсианское.

Насправді неможливість повного виконання умов адек-ватності концептуальних моделей і математично записаних емпіричних залежностей часто призводить до ослаблення вимог до істинності одержуваних математичних макромоделей. Безліч з-Вестн і описаних в Нині макроекономічних ефектів вимагають більш детального опису за допомогою методів, складових формальний підхід до макроекономічного моделювання. Для цього слід формалізувати основні макроекономічні концепції (концептуальні моделі макроекономічних елементів), що входять до загальний контур реакції виробників і споживачів на зміну цін.

Основу всіх сучасних макроекономічних концепцій становлять деякі важливі мікроекономічні концепції, на основі яких і формуються макроекономічні концепції нижчого рівня - концеп-ції мотивації економічних агентів БФ і ДХ.

У результаті аналізу моделей і методів макроекономічного моделювання виявляються деякі важливі проблеми використання математичної теорії вибору в умовах невизначеності в макроекономічних моделях. Викладаються методологічні основи сучасних і перспективних макроекономічних концепцій.

Спочатку окремо розглядаються основи і проблематика концепцій вищого (макроекономічного) і нижчого (мікроекономічного) рівнів. Далі, як результат композиції цих концепцій, розглядається проблематика моделей загальної економічної рівноваги і методологія теорії суспільного вибору. При цьому деталізується концептуальна модель загальної економічної рівноваги і математична модель суспільного вибору.

На закінчення на підставі аналізу існуючих моделей виявляється проблематика синтезу моделей загальної економічної рівноваги, синтезу макроекономічних концептуальних моделей, а також проблематика дослідження закономірностей макроекономічних взаємозв'язків з урахуванням факторів невизначеності.

2. Розробка засобів макроекономічного моделювання

Розглянуто нечітко-імовірнісні методи досліджень і глобальна проблема оцінювання можливостей в задачах моделювання макроекономіки. на підставі аналізу економіко-математичної методології моделювання з використанням методів декомпозиції відносин, а також з використанням методів декомпозиції відображень розглядаються підходи до формалізованого поданням моделей загальної економічної рівноваги [3].

Обгрунтовується перехід від класичної формалізації моделей загальної економічної рівноваги до формалізованих неокласичним і неокейнсианским моделям, що дозволяє враховувати різні фактори невизначеності і забезпечити коректність зближення мікро- і макроекономічних моделей. З цією метою розробляється концепція нечіткої заходи, а також узагальнений нечітко-возможностний підхід до моделювання макроекономіки.

Cогласно загальним уявленням системного підходу невизначеність, як основний супутній фактор при вирішенні питання складності, виявляється також складно структурованим поняттям і одним з найважливіших інструментів забезпечення адекватності висновків досліджень реально відбувається в економіці процесам. Внаслідок багатозначності факторів невизначеності операції з числовими оцінками невизначеності, якщо такі можна представити в рамках теоретико-множинного підходу, мають сенс тільки в тому випадку, коли ці оцінки відображають один, і тільки один фактор (або загальну групу факто-рів) невизначеності для всіх що беруть участь в операції операндів. Для обліку цієї особливості в економічній предметної області запропоновано нову трактування парадигми невизначеності [4].

У такому трактуванні детермінованість в необхідному значенні парадигм Канта і Л. Заде формується двома факторами: власне фактором необ-хідності (правдоподібність) і аксіологічними фактором (нечітко-полезностний). При цьому враховується, що аксіологічний фактор пов'язаний з нечіткої оцінкою альтернатив, а поссібіліческій - з нечіткою оцінкою структури предмету. Переходи від можливості до дійсності розглядаються через лінгвістичну невизначеність з будь-якого з двох пу-тей. При переході власне через невизначеність лінгвістичний ас-пект може включати як окремий випадок не тільки поссібіліческую, але і вірогідну невизначеність. При переході через детермінованість лінгвістичний аспект як окремий випадок включає правдоподібність (необхідність в сенсі Канта) і аксиологическую (нечітко-полезностную) невизначеність.

Для формалізації нової парадигми невизначеності пропонується визначення лінгвістичного возможностно-полезностного простору, в якому досліджується перетворення можливості в дійсність.

На основі аналізу категорій невизначеності, використовуваних при дослідженні складних систем, пропонується відповідна математична структура в задачах моделювання економічних систем з урахуванням факторів невизначеності. Аналізуються основні шляхи та методи вирішення завдань нечіткої оптимізації в моделях мотивації економічних суб'єктів [5].

3. Дослідження можливості застосування інструментарію нечіткої алгебри для розрахунків

З урахуванням обраних у другому розділі напрямів і сформульованих вимог до макроекономічного моделювання викладаються основи створення спеціального математичного інструментарію нечіткої алгебри в цілях моделювання процесів у складних економічних системах.

Останнім часом для математичного опису нечітких чисел все ширше використовується поняття і відповідний апарат нечіткого преди-ката можливостей. Для виконання практичних розрахунків з нечіткими числами необхідно задати дві елементарні алгебри: алгебру ариф-тичні бінарних операцій ("складання", "віднімання", множення "і" поділ ") і алгебру логічних бінарних операцій (" більше "," менше "," дорівнює "і їх похідні). Пропонується в якості основи алгебри арифметичних операцій з нечіткими числами застосовувати принцип узагальнення, згідно з яким результатом будь нечіткої операції повинно бути нечітке число, визначене в тій же формі [6].

Для цього на основі поняття нечіткого числа і операцій з нечіткими числами розробляється математичний опис бінарних алгебраїчних і логічних операцій з нечіткими числами. Як узагальнення цих математичних конструкцій розробляється інструментарій нечіткої алгебри на основі предикатних сумішей. При цьому загальні визначення основних алгебраїчних операцій на сумішах конкретизуються розробкою нечітких бінарних алгебраїчних операцій, заданих на базових множинах лінійними рівневими функціями аргументів.

Алгебра арифметичних операцій з нечіткими числами може служити математичною моделлю розрахунку показника вибору в процесі прийняття суб'єктивного рішення ДХ або БФ. При цьому введення предикатной суміші у вигляді деякої математичної функції відкриває широкі можливості до статистичному підтвердженню адекватності введеної алгебри операцій з нечіткими числами і реальному розумовому процесу вибору конкретного макроекономічного суб'єкта. Однак застосування менш точного і "надійного" ??суб'єктивного вибору на практиці виправдано лише тоді, коли більш точний і "надійний" об'єктивно вибір з яких-небудь причин неможливий [7].

Основною відмінністю визначеного на предикатних сумішах математ-тичного апарату алгебраїчних операцій з нечіткими числами є наявність трьох протиріч.

Далі проводяться дослідження розробленого математичного інструментарію. Спочатку досліджується методика логіко-алгебраїчних обчислень в економічних моделях з нечіткими параметрами. Потім аналізуються основні властивості нечітких алгебраїчних бінарних операцій.

4. Розробка методичного забезпечення для вирішення макроекономічних завдань із застосуванням нечітко-ймовірнісного математичного інструментарію

На основі методології, викладеної у попередніх розділах, розглядаються деякі важливі прикладні результати застосування нечітко-імовірнісного підходу до вирішення макроекономічних завдань. Зокрема, розглядається рішення задач вибору структури акціонерного капіталу за наявності нечіткої інформації про прибутковість цінних паперів, узагальнене в теоремі Міллера-Модільяні (ММ). На основі аналізу класичної формулювання теореми ММ і таких факторів сучасної економічної дійсності, як вплив індивідуальної ставки за кредитами для інвесторів і вплив відмінностей у відсоткових ставках за облігаціями дається нова нечітке формулювання теореми ММ, позбавлена ??недоліків традиційних детермінованою і стохастичною постановок.

Відома класична методика вибору структури акціонерного капі-тала на основі рішення завдань оцінювання вартості БФ зводиться до доказів-тельству інваріантності вартості БФ стосовно структурі її капі-тала (теорема ММ), має не тільки сильні, але і слабкі сторони. Перед-Викладено корекція цього доказу і формулювання теореми ММ, ос-Нова на введенні допусків і застосуванні методів нечіткої алгебри. Необхідність у деякої коригування класичного докази (відзначена ще самими авторами ММ) пояснюється тим, що виконати одну з основних припущень теореми ММ на реальному ринку капіталу виявляється неможливо. В результаті доказ, побудоване, в част-ності, на тому підставі, що інвестори (як ДХ) можуть отримувати кредити під ті ж відсотки, що й юридичні особи - БФ, або що ставки за обли-гаціям зрівняються зі ставками за кредитами, стає неочевидним і цілком може бути спростовано.

На закінчення розглядається рішення завдань лінійного лінгвістичного розпізнавання стану економічних агентів при нечіткому описі фінансово-економічних параметрів. Розробляються загальні положення методу лінгвістичного розпізнавання і пропонуються нові взаємопов'язані підходи з використанням як двомірних, так і багатовимірних моделей невизначених параметрів розпізнавання.

Розглядаються питання застосування розробленого в третьому розділі інструментарію оперування з нечіткими числами для формування лінеаризованих подання шкали якості лінгвістичного розпізнавання.

Висновки

У процесі дослідження теми магістрської роботи були виявлені основні проблеми підвищення адекватності моделей і методів макроекономічного, моделювання; розроблені засоби макроекономічного моделювання, прикладні можливості яких орієнтовані на широке застосування нечітко-возможностного математичного апарату; досліджено можливості застосування інструментарію нечіткої алгебри для розрахунків. Надалі планується розробити методичне забезпечення для вирішення макроекономічних завдань із застосуванням нечітко-возможностного математичного інструментарію.

Перелік посилань

  1. Вечканов Г.С. Экономическая теория: Учебник для вузов. 3-е изд. Стандарт третьего поколения. — СПб.: Питер, 2011. — 512с.
  2. Вечканов Г.С., Вечканова Г.Р. Макроэкономика. Завтра экзамен. 8-е изд. — СПб.: Питер, 2008. — 288 с.
  3. Акаев А.А., Гринберг Р.С., Гринин Л.Е., Коротаев А.В., Малков С.Ю. Кондратьевские волны: аспекты и перспективы: ежегодник / Отв. ред. Акаев А.А., Гринберг Р.С., Гринин Л.Е., Коротаев А.В., Малков С.Ю. — Влгоград: Учитель, 2012. — 384с.
  4. Кононова Л.О.. Чорноус Л.В., Скопенко Н.С. Економетрія: конспект лекцій / Л.О. Кононова, Л.В. Чорноус, Н.С.Скопенко. — К: НУХТ, 2010. — 144 с.
  5. Радионов Н.В. Модели эффективности инвестиций и кредитования. Часть 1. Основы финансового анализа: Монография. — СПб.: Наука, 2005. — 37,5 п.л.
  6. Бородич С.А. Вводный курс эконометрики / С.А.Бородич. — Мн.:БГУ, 2000. — 354 с.
  7. Плотников В.В. Основы эконометрики / В.В. Плотников. — Владивосток: ДВГАЭУ, 2003.