Назад в библиотеку

---

Кольчик С.О.

Научн. руководитель д.э.н., проф., Румянцев Н.В.

Институт информатики и искусственного интеллекта ДонНТУ

Применение вейвлет-фильтрации для обработки финансовых данных

Задача прогнозирования поведения сложных динамических систем в экономике является трудноформализуемой. В каждой реальной задаче присутствует шум, и необходимо уметь справляться с ним. В финансовых приложениях данные зашумлены особенно сильно. Поэтому для успешного прогнозирования необходима эффективная обработка входных данных, в частности, минимизация влияния случайных флуктуаций и шума на конечный результат. Понизить шумовую составляющую можно прибегнув к вейвлет-анализу.

Целью данной работы является обоснование использования методов вейвлет-анализа для моделирования динамики развития индикаторов, характеризующих финансовый рынок.

Объектом исследования выступает динамика индексов рынка, предметом - методы вейвлет-преобразования сигналов.

Значительный вклад в развитие теории вейвлетов внесла американский ученый Ингрид Добеши.

Следует отметить, что использование методов вейвлет-преобразования сигналов именно в сфере экономических наук получило распространение в большей степени в работах зарубежных исследователей. При этом основными направлениями использования определенного метода является декомпозиция рядов и исследование взаимосвязи между экономическими индикаторами.

Несмотря на значительное количество разработок в области вейвлет-преобразования сигналов, применение этого инструментария для анализа экономических динамических рядов нуждается в совершенствовании.

Вейвлет-преобразование однородного сигнала строится на его разложении по базису, который сформирован из масштабирующей функции путем масштабных изменений и переносов [3]. Каждая из функций этого базиса характеризует как определенную пространственную частоту, так и ее локализацию во времени. Таким образом, в отличие от преобразования Фурье, вейвлет-преобразование обеспечивает двумерное представление одномерного сигнала, при этом частота и координата рассматриваются как независимые переменные. Данная особенность вейвлет-преобразования сигналов подчеркивает возможность их использования для численного моделирования как иерархический базис, приспособленный для описания динамики сложных нелинейных процессов, характеризующихся взаимодействием возмущений в широких диапазонах пространственных и временных частот [1].

Разложение дискретного временного ряда на соответствующие уровни разрешения m выполняется по формуле:

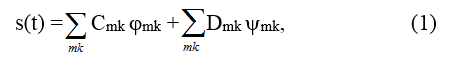
где      s(t) – исходный сигнал;

С_mk – аппроксимирующие коэффициенты;

D_mk – детализирующие коэффициенты;

j_mk – форма вейвлет-функции;

y_mk – форма масштабирующей функции.

Заданный алгоритм имеет древовидную структуру: на каждом шаге отсеиваются детализирующие коэффициенты D_mk, а дальнейший анализ происходит с аппроксимирующими коэффициентами C_mk (см. рис. 1)

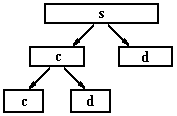
Рисунок 1. Дерево разложения исходного сигнала

Полученные при разложении аппроксимирующие коэффициенты представляют сглаженный сигнал, а детализирующие коэффициенты описывают колебания. Следовательно, шумовая компонента больше отражается в детализирующих коэффициентах D_mk. Поэтому при удалении шума обрабатывают обычно детализирующие коэффициенты. Удаление шума реализуется с помощью метода пороговой обработки коэффициентов (трешолдинг) и заключается в обнулении значений коэффициентов, меньших некоторого порогового значения [2].

Для примера возьмем дневные данные о ценах валютного курса евро\доллар. Перед использованием эти массивы данных были предварительно обработаны.

Полученный сигнал имеет шумовую компоненту, поэтому сначала необходимо вычислить порог для удаления шума, после необходимо удалить шум и оценить фрактальность сигнала. Для удаления шума используем вейвлет Добеши четвертого порядка (db4), уровень разложения 3. Исходный и очищенный сигнал изображены на рисунке 2. Реализация поставленных задач производилась в среде MATLAB 7.12 Wavelet Toolbox.

При этом в очищенном сигнале (отмечен точками) колебания цены видны более явно, хорошо отражена их форма и направленность, что позволяет четче идентифицировать фигуры технического анализа на графике. Очищенный от шума сигнал удобно использовать для обучения нейронных сетей с целью прогнозирования тренда.

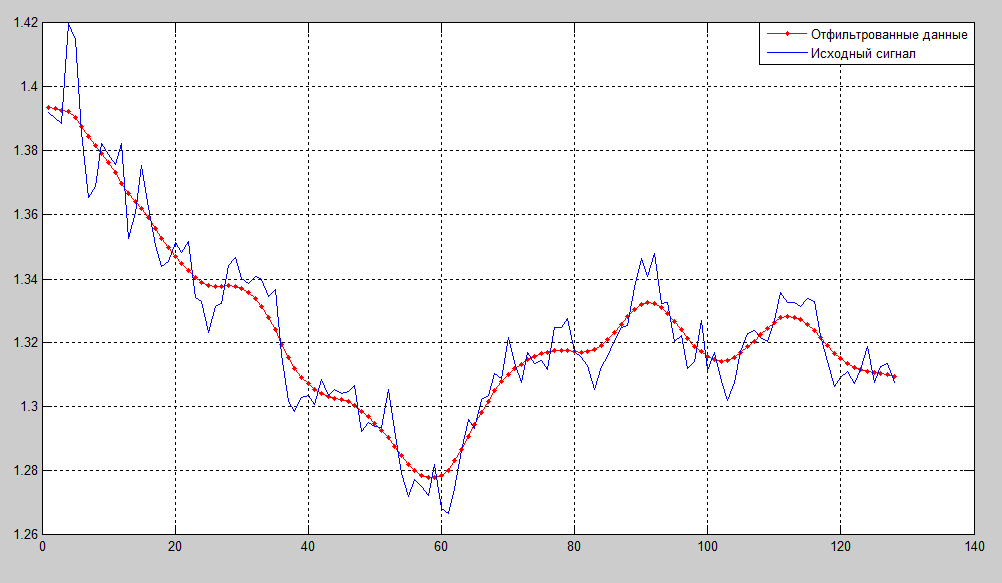
Рисунок 2. Исходный и очищенный сигнал

Можно также получить всю удаленную шумовую компоненту в виде разности исходного сигнала и очищенного. Шумовая компонента может быть использована для получения статистических и стохастических характеристик высокочастотной части сигнала. Например, из шумовой составляющей.

В представленной работе был проведен анализ финансовых временных рядов на основе вейвлет-преобразования, определены возможности и основные преимущества метода вейвлет-разложение сигнала, основной из которых является его частотно-временная локализация. Также рассмотрена возможность подавления шумовой составляющей и флуктуаций в рядах, извлечение наиболее значимых для предсказания признаков. На основе данной работы можно сделать вывод об эффективности применения вейвлет-анализа в качестве математического аппарата для обработки и фильтрации финансовых данных.

ЛИТЕРАТУРА

1. Crowley P. M., Lee J. Deconposing the co-movement of the business cycle: a time-frequency analysis of growth cycles in the euro zone. – Macroeconomics, 2005. - 73
2. Новиков Л.В. Основы вейвлет-анализа сигналов/Л.В. Новиков. – СПб., 1999. – 342 с.
3. Добеши И. Десять лекций по вейвлетам/Добеши И. – Ижевск: 2001. – 464 с.