Автор: Моспан А.А., Назарова И.А.
Источник: Конференция «Информационные управляющие системы и компьютерный мониторинг»,
Донецкий национальный технический университет, май 2010 г.
Моспан А.А., Назарова И.А. Реализация паутинообразных моделей динамики цен на основе программного пакета «E&F Chaos». В статье рассмотрены несколько видов паутинообразной модели ценообразования для исследования динамики рыночных цен. Приведен пример построения и исследования модели с помощью программы «E&F Chaos», которая позволяет более подробно изучить процессы образования цен и достижение оптимальной равновесной цены; представить графически изменения цен, поведение ценовой функции; предсказать хаотический процесс цен; быть полезным основанием для составления качественных рекомендаций для основных игроков рынка.
Модели нахождения оптимума в задачах «спрос-предложение» не теряют своей актуальности и в настоящее время. К такому классу моделей относится паутинообразная модель ценообразования. Данная модель является пригодной как в условиях стабильной рыночной экономики, так и в период ее становления (пример, Украина). С помощью паутинообразной модели появляется возможность более эффективной адаптации предприятиям к рыночным условиям. Поэтому исследования в данной области представляют особый интерес для нашей страны.
Проблема прогнозирования равновесной рыночной цены является одной из важных и наиболее сложных в экономической теории. Одним из подходов к решению этой задачи является анализ кривых спроса и предложения. Такой подход является широко используемым представителями экономической теории и имеет под собой серьезную основу. Суть его заключается в анализе кривых спроса и предложения, для нахождения точки рыночного равновесия. Однако достижение точки равновесия еще не гарантирует устойчивости, в действительности само равновесие является исключением из правил. Чаще всего наблюдаются колебания уровня цен и объемов выпуска продукции. Таким образом, равновесная точка постоянно находится в подвижном состоянии, и статические графики оказываются бесполезными при составлении прогнозов. Поэтому к настоящему моменту разрабатываются различные программные продукты, позволяющие подходить к исследованию спроса и предложения на рынке более динамично. Одним из таких пакетов и является Economics&Finance Chaos, разработанный в Центре нелинейной динамики в экономике и финансах (Center for Nonlinear Dynamics in Economics and Finance, CeNDEF) в Амстердаме (Нидерлады) [1-2]<./p>
В данной работе представлено несколько видов паутинообразной модели ценообразования, а также реализация и исследование нелинейной модели динамики цен на рынках недвижимости и земли на базе программного пакета E&F Chaos.
Для моделирования данной модели воспользуемся программным пакетом E&F Chaos. Представленное программное обеспечение позволяет провести основательный анализ над моделями, используя широкий набор инструментов для построения различных графиков. Первым приведем диаграмму графического анализа, которая и отображает вид паутинообразной модели (см. рис. 1). Используя этот метод графического анализа можно легко и наглядно отобразить механизм определения новой точки, приближающейся или отдаляющейся от равновесной
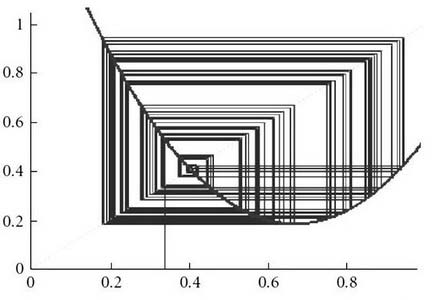
Рис. 1 – «Паутинообразная» модель рынка недвижимости, при заданных параметрах
В паутинообразной модели поведение рыночных цен может быть хаотичным. График, изображенный на рис. 2, показывает хаотические изменения цены на недвижимость во времени или, другими словами, чувствительность цен во времени.
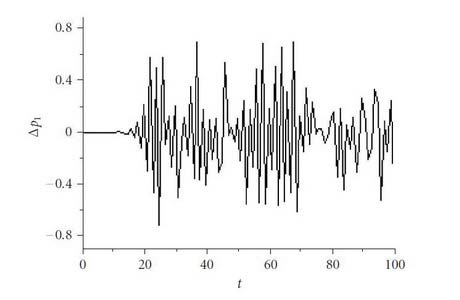
Рис. 2 – Чувствительность цены на недвижимость Р1 во времени
E&F Chaos позволяет построить 2-D диаграмму бифуркаций «Bifurcation diagram» логистического отображения. Для получения такого графика необходимо выбрать какой-нибудь параметр модели, задать его минимальное и максимальное значения, и выбрать переменную. Эта диаграмма (рис.3) показывает движение динамической системы, в данном случае переменными являются цены на землю и недвижимость.
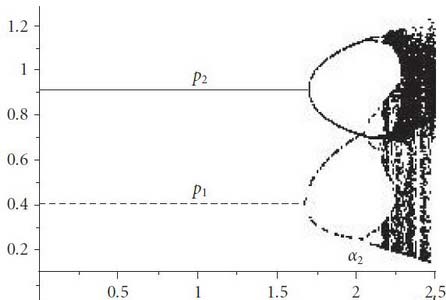
Рис. 3 – Диаграмма бифуркаций на временном интервале P1 и P2, при ?2=0,4
Диаграмма бифуркаций показывает, что равновесие по Нэшу устанавливается на уровне E*=(0.4,0.9) и является локально устойчивым для маленьких значений ?1 и ?2. Если ?1 будет возрастать, то точка равновесия по Нэшу станет не стабильной, и будет наблюдаться комплексное динамическое поведение (циклы высокого порядка и хаос).
Мощным численным инструментом пакета E&F Chaos является построение диаграммы максимальных экспонент Ляпунова. Экспонента Ляпунова предназначена для определения, является ли динамическое поведение системы хаотическим, и оценивает скорость расхождения (сближения) траекторий вдоль разных координатных направлений. Алгоритм вычисления экспоненты Ляпунова описан в [4].
Для еще более глубоко анализа можно также построить графики аттракторов для разных значений ?2. На рисунке 4 представлен такой график с параметром ?2 равным 0,1.
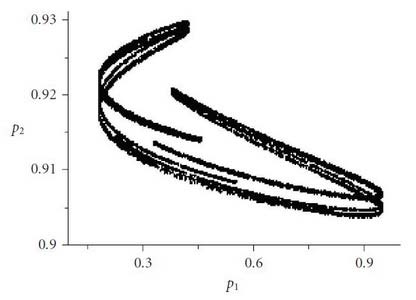
Рис. 4 – Аттрактор для ?2 = 0.1
Диаграммы аттракторов содержат информацию о долгосрочном динамическом поведении системы. Вид представленного хаотического аттрактора согласно программе, говорит о его фрактальной структуре.
Исходя из исследований, проведенных на представленной модели, было определено, что изменение цены предлагаемых земельных участков имеет значительное влияние на рынок недвижимости. Следовательно, динамика рынка меняется, в случае применения «игроками» разной скорости его перестройки. Перспективным направлением исследований является построение и исследование паутинообразной модели динамики цен, в случае участия в рыночных отношениях гетерогенных производителей.
1. Center for Nonlinear Dynamics in Economics and Finance. – Режим доступа: http://www1.fee.uva.nl/cendef/ CeNDEF.
2.Diks C., Hommes C., Panchenko V., Roy van der Weide Art. E&F Chaos: A User Friendly Software Package for Nonlinear Economic Dynamics // Comp. econom.
3. Junhai Ma, LingLing Mu Art. Complex Dynamics in a Nonlinear Cobweb Model for Real Estate Market // Journal of Applied Mathematics and Decision Siences. - 2007.
4. Wolf A., Swift J. B., Swinney, L., Vastano J. A. Determining Lyapunov exponents from a time series // Physica D, v.16. 1985.