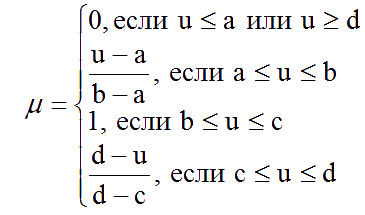Шабля А.И., Донец А.С. - Разработка систем нечетких баз знаний в управлении риском страховых компаний

Аннотация

Шабля А.И., Донец А.С. Разработка систем нечетких баз знаний в управлении риском страховых компаний. Статья посвящена разработке модели оценки страхового риска на основе методов нечеткой логики, которая представляет собой гибкую систему управления риском в страховой деятельности.

Общая постановка проблемы

Любая сфера экономической деятельности сопровождается явлением риска. Страхование относится к тем видам деятельности, которые сильно подвержены этому явлению. Фактор риска и необходимость покрытия возможного ущерба в результате его проявления вызывают потребность в страховании.

Точное измерение риска осуществляется различными количественными методами: математическими, статистическими, методами теории вероятности, теорией игр и многие другие. Риск в страховании сопровожден большой мерой неопределенности, отсутствием выраженной закономерности и его невозможно задать четкими числовыми данными. Эти факторы ограничивают использование классических методов статистического анализа и возникает необходимость разработки новых методов оценки, к которым можно отнести системы с нечеткой логикой.

Основной материал

Для эффективного определения размера страховой суммы, необходимо разработать комплексный подход к оценке страхового риска. Методологический аппарат нечеткой логики позволяет аналитически обосновать сумму страховой выплаты и рационально разграничить клиентов на группы риска. Это становится возможным благодаря созданию систем нечетких баз знаний.

Вероятность наступления страхового события определяется апостериори, т.е. исходя из прошлого опыта. В классической теории нетто-ставка, исчисляемая в процентах, является вероятностью наступления страхового события.

Характерной особенностью страховых рисков является неполнота исходной информации, отсутствие нормального распределения среди статистических данных, что является сдерживающим фактором использования классических методов математической статистики. Возникает необходимость в новых методах, и в их числе – методы нечеткой логики. Их основные особенности:

возможность работы с априорно неопределенной информацией;
учет количественных и качественных пременных и критериев;
возможность внедрения знаний эксперта в виде соотвествующих правил вывода;
возможность обучения системы в процессе эксплуатации.

Первым шагом в созданиимодели оценки страхового риска необходимо определиться в предметной области. Пусть требуется оценить наиболее вероятный страховой случай и определить меру этой вероятности в области личного страхования. Страхование от несчастного случая – виды страхования, где в качестве страхового случая предусматривается внешняя причина, как правило, кратковременного воздействия, приведшая к временной или постоянной потере трудоспособности, или смерти застрахованного. В отличие от страхования жизни, которое, как правило, носит долговременный характер (от нескольких лет до нескольких десятков лет), страхование от несчастного случая заключаются, как правило, на срок до одного года. Следовательно, исходным множеством переменных выхода являются следующие страховые случаи:

Y1: травма застрахованного лица в результате несчастного случая {0-100%};

Y2: признание застрахованного лица инвалидом {0-100%};

Y3: временная утрата трудоспособности {0-100%};

Y4: смерть {0-100%};

Определеим исходное множество лингвистических переменных Х по различным критериям:

Х1: возраст {молодой, средних лет, старый};

Х2: размер семьи {маленькая, средняя, большая};

Х3: условия работы {оптимальные, допустимые, вредные, опасные};

Эти переменные задаются в виде функции принадлежности, выбор которых зависит от разработчика базы знаний. Зачастую используются функции Гаусса, трапецевидная функция и многие другие. В данном случае используется трапецевидная функция:

Формула трапецевидной функции принадлежности

(a,d) – носитель нечеткого множества – пессимистическая оценка нечеткого числа;

[b,c] – ядро нечеткого множества – оптимистическа оценка нечеткого числа.

Будем считать, что известны экспериментальные зависимости Y от X. Задача обучения нечеткой базе знаний Сугено сводится к поиску вектора (P, B), который обеспечивает следующий принцип (2):

где P – вектор параметров функций принадлежности нечетких термов;

B – вектор коэффициентов в заключениях правил;

F(P, B, X_r ) – результат логического вывода для входного вектора X_r по нечеткой модели с параметрами (P, B).

Для того, чтобы обучить нечеткую базу знаний по данному критерию, воспользуемся ANFIS-редактором. Он позволяет автоматически синтезировать из эксперементальных данных нейро-нечеткие сети. Нейро-нечеткую сеть можно рассматривать как одну из разновидностей систем нечеткого логического вывода типа Сугено. При этому функции принадлежности синтезированных систем настроены так, чтобы минимизировать отклонения между результатами нечеткого моделирования и эксперементальными данными.

Пусть имеется обучающая выборка из 40 данных (таблица 1). В ней представлены значения факторов: возраст, размер семьи на содержании клиента, коэффициент условий труда, наличие авто, количество выплат клиентам со 100 договоров, которые получили инвалидность.

Таблица 1. Обучающая выборка

Возраст	Размер семьи	Коэффицинт условий труда	Наличие автомобиля	Количество тех, кто стал инвалидом из 100 застрахованных от данного случая.
30	1	0.29	0	0.03
59	2	0.77	0	0.02
36	0	0.39	1	0.02
54	0	0.69	1	0.04
52	1	0.66	1	0.03
35	2	0.38	1	0.01
60	2	0.79	1	0.07
...	...	...	...	...
37	0	0.26	1	0.01
32	0	0.33	1	0.01
44	2	0.53	0	0.03
39	2	0.45	1	0.03
27	1	0.26	1	0.01
40	1	0.37	0	0.02

Используя программный пакет Matlab в рабочей области создаем 2 файла с переменными, которые включают обучающую и тестовые выборки. В тестовую выборку включаем 20 данных. Открывая окно fuzzy и в базе знаний Сугено ANFIS редактор, загружаем исходные данные (рис.1)

Рисунок 1. Обучаюшая и тестовая выборки

Данные в области визуализации результаты моделирования выводятся в виде множества точек в двумерном пространстве. При этом по оси абсцисс откладывается порядковый номер строчки данных в выборке (обучающей, тестирующей или контрольной), а по оси ординат — значение выходной переменной для данной строчки выборки. Экспериментальным данным соответствует маркер кружков, а тестовым — точки.

В области обучения (Train FIS) расположены меню выбора метода оптимизации (Optim. method), поле задания требуемой точности обучения (Error tolerance), поле задания количества итераций обучения (Epochs) и кнопка Train Now, нажатие которой запускает режим обучение. Промежуточные результаты обучения выводятся в область визуализации и в рабочую области MatLab. В ANFIS-редакторе реализованы два метода обучения: backpropa – метод обратного распространения ошибки, основанный на идеях метода наискорейшего спуска; hybrid – гибридный метод, объединяющий метод обратного распространения ошибки с методом наименьших квадратов.

Выбран метод hybrid. Создаем исходную систему нечеткого вывода. По умалчиванию используется метод решетчетого разбиения, согласно которому функции принадлежности нечетких термов равномерно распределяются внутри диапазона изменения данных. База знаний содержит все возможные варианты правил. Коэффициенты в заключениях правил равны нулю.

Следующий шаг – обучение базы знаний по критерию (2). Для этого необходимо указать число итераций. Выбираем 7 итераций и в итоге система проходит обучение.

Для проверки модели на тестовой выборке необходимо переключиться на тестовый режим. В итоге, в области визуализации появится следующий график (рис.2)

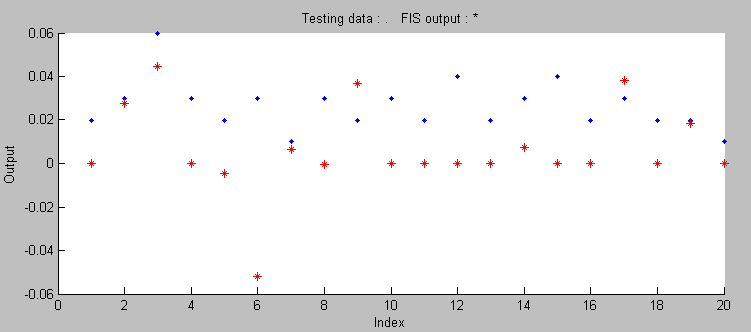
Рисунок 2. Тестирование нечеткой системы

Ошибка тестовой выборки составляет 0,028. Экспериментальные данные показаны точками, а результаты моделирования – звездочками. После того, как была составлена база знаний Сугено, можно выявить ряд закономерностей между входящими переменными и выводом. Для этого можно воспользоваться визуализацией правил и редактор строит поверхность (рис.3)

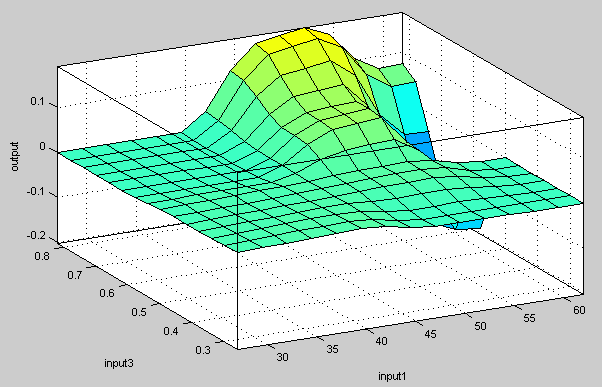
Рисунок 3. Поверхность для страхового случая «Инвалидность»

Для факторов «Условия труда» и «Возраст» поверхность принимает вид возвышенности и впадины. При этом максимальное значение приходится на высокий коэффициент условий труда и возраст человека 40-50 лет. Для страхового случая «Инвалидность» эти люди наиболее рискованные требуют и особого подхода. Оставшиеся 3 базы знаний формируются аналогичным способом.

Таким образом, база знаний – важный компонент интеллектуальной системы. Наиболее известный класс таких программ — это экспертные системы. Они предназначены для поиска способов решения проблем из некоторой предметной области, основываясь на записях базы знаний и на пользовательском описании ситуации.

Простые базы знаний могут использоваться для создания экспертных систем хранения данных в организации: документации, руководств, статей технического обеспечения. Главная цель создания таких баз – помочь менее опытным людям найти уже существующее описание способа решения какой-либо проблемы.

После того, как составлена база знаний, необходимо выбрать оболочку ее реализации. Программа Simulink является приложением к пакету MATLAB. При моделировании с использованием Simulink реализуется принцип визуального программирования, в соответствии с которым, пользователь на экране из библиотеки стандартных блоков создает модель устройства и осуществляет расчеты. При этом, в отличие от классических способов моделирования, пользователю не нужно досконально изучать язык программирования и численные методы математики, а достаточно общих знаний, требующихся при работе на компьютере и знаний той предметной области, в которой он работает

Представим составленную базу знаний в виде системы (рис.4)

Рисунок 4. Представление базы знаний в оболочке Simulink

Таким образом, данная модель предстваляет собой экспертную систему. Основное предназначение модели заключается в комплексной оценки страхового риска. Преимуществом приведенного подхода является числовая оценка различных страховых случаев, что позволяет качественно улучшить риск-менеджмент страховщика, надежнее контролировать рисковую позицию компании, эффективно управлять страховой деятельностью и обеспечивать финансовую устойчивость страховщика. Недостаток модели заключается трансформации качественных показателей в количественные, что может внести неточности.

Выводы

Поскольку риск представляет собой величину неопределенную и зачастую не подвластную численной оценке, то это придает модели субъективный характер. Эффективное управление риском страхования требует использования соответствующих требованиям методик и классификаций, что способствует оптимизации процесса принятия дальнейших управленческих решений, связанных с рисками и поиска путей их минимизации.

Выделенные и организованные в виде отдельных, целостных структур информационного обеспечения знания о предметной области становятся явными и отделяются от других типов знаний, например общих знаний. Базы знаний позволяют выполнять рассуждения не только и не столько на основе формальной (математической) логики, но и на основе опыта, фактов, эвристик, т.е. они приближены к человеческой логике. Разработки в области искусственного интеллекта имеют целью использование больших объемов высококачественных специальных знаний о некоторой узкой предметной области для решения сложных, неординарных задач

База знаний является основой экспертной системы, она накапливается в процессе ее построения. Знания выражаются в явном виде, позволяющем сделать явным способ мышления и решения задач, и организованы так, чтобы упростить принятие решений. База знаний, обусловливающая компетентность экспертной системы, воплощает в себе знания специалистов учреждения, отдела, опыт группы специалистов и представляет собой институциональные знания.

Список использованной литературы

1. Штовба С.Д. Проектирование нечетких систем средствами Matlab. – М.: Горячая линия – Телеком, 2007.– с.33
2. Нечипоренко В. Страховой риск: отдельные вопросы толкования, правового определения, менеджмента // Финансовые услуги.– 2001.– №1–2. – С. 38–43.
3. Гутко Л.М. Страховий ринок Украхни: Стан, проблеми розвитку та шляхи їх вирішення//Менеджент: Оцінка страхового ризику №4, – 2009 рік
4. Цисаря И.Ф. MATLAB Simulink. Компьютерное моделирование экономики. – М.: Солон-Пресс, 2008. – 256с.
5. И.В. Черных Simulink. Среда создания инженерных приложений. – М.: Диалог-МИФИ, 2004. – 496 с.
6. В. Г. Потемкина. Вычисления в среде MATLAB. – М.: Диалог-МИФИ, 2004. – 720 с.