Анализ финансового состояния и прогнозирования риска банкротства корпорации в условиях неопределенности

Аннотация

Ови Нафас Асаи Аг Гамиш, Юрий Зайченко – Анализ финансового состояния и прогнозирования риска банкротства корпорации в условиях неопределенности. Рассмотрена проблема прогнозирования риска банкротства. Приведены методы дискриминантного анализа, а также матричный метод на основе нечеткой логики.

Введение

Одной из актуальных проблем, связанных со стратегическим менеджментом и планированием является анализфинансового состояния и оценка риска банкротства предприятия (корпорации). Своевременное выявление признаков возможного банкротства позволяет руководству принимать срочные меры по исправлениюфинансового состояния и снижениюриска банкротства.

В течение многих лет классические статистические методы широко использовались для прогнозирования рисков банкротства. Эти модели также имеют название одномерных (single-period) методов классификации. Они включают процедуру классификации, которая относит ту или другую компанию к группе потенциальных банкротов или к группе компаний с благоприятным финансовым положением с определенной мерой точности. Применяя эти модели, могут возникать два типа ошибок. Ошибка первого типа возникает тогда, когда фирма-банкрот классифицировалась как фирма с благоприятным финансовым положением. Ошибка второго типа возникает тогда, когда предприятие с нормальным финансовым состоянием классифицируется как потенциальный банкрот. Обе ошибки могут привести к серьезным последствиям и убыткам. Например, если кредитное учреждение откажет компаниям со «здоровой» финансовой ситуацией в предоставлении кредита в связи с допущением ошибки 2-го типа, то это может привести к потерям будущей прибыли этой компанией. Такую ошибку часто называют «коммерческим риском». И наоборот, если кредитное учреждение примет решение о предоставлении кредита компании, которая является потенциальным банкротом (ошибка 1-го типа), то это может привести к потерям процентов по кредиту, значительной части ссудных средств, альтернативной стоимости, и другие. Поэтому такую ошибку называют «кредитным риском».

В настоящее время существует несколько общепризнанных статистических методов и методик оценки риска банкротства. Наиболее известной и широко применяемой является методика профессора Альтмана. Вместе с тем, модель Альтмана имеет ряд недостатков, и ее применение для экономики Украины сопряжено с определенными трудностями. Поэтому в последние годы разрабатываются альтернативные подходы и методы, учитывающие специфику анализа и принятия решений в условиях неопределенности. К их числу относятся аппарат нечетких множеств и нечеткие нейронные сети.

Целью настоящей работы является рассмотрение и сравнительный анализ эффективности применения различных методов и подходов к прогнозированию риска банкротства предприятий применительно к экономике Украины.

Основной материал

К числу наиболее известных и распространенных моделей оценки риска банкротства относится модель профессора Е. Альтмана.

Модель Альтмана построена с использованием аппарата мультипликативного дискриминантного анализа (МДА), который позволяет подобрать такие показатели, дисперсия которых между группами была бы максимальной, а внутри группы минимальной. В данном случае классификация проводилась по двум группам компаний, одни из которых позднее обанкротились, а другие, наоборот, смогли выстоять и упрочить своефинансовое положение.

В результате МДА была построена модель Альтмана (Z-счет), имеющая следующий вид:

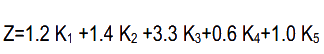
Где K1 = собственный оборотный капитал/ сумма активов;

K2 = нераспределенная прибыль/ сумма активов;

K3 = прибыль до уплаты процентов/ сумма активов;

K4 = рыночная стоимость собственного капитала/ стоимость заемного капитала;

В результате проведения дискриминантного анализа по группе предприятий, которые заявили о своем банкротстве, по финансовых показателям, взятым за год до дефолта, был верно смоделирован этот факт в 31 случае из 33 (94,5%), и в 2 – сделана ошибка (6%). По второй группе предприятий, которые не обанкротились, модель ошибочно спрогнозировала банкротство только в 1 случае (3%), а в оставшихся 32 (97%) была допущена очень низкая вероятность банкротства, что и подтвердилось фактически. Соответствующие результаты приведены в таблице 1.

Таблица 1. Прогнозные значения риска банкротства

Группа	Количество компаний	Прогноз: прнадлежность к первой группе	Прогноз: принадлежность ко второй группе)
Группа 1 (обанкротившиеся компании)	33	31 (94%)	2 (6%)
Группа 2 (компании не обанкротились)	33	1 (3%)	32 (97%)

Слабая сторона модели Альтмана состоит в том, что модель является чисто эмпирической, подогнанной по выборке, и не имеет под собой самостоятельной теоретической базы. Кроме того, приведенные коэффициенты должны определяться для различных отраслей промышленности и будут естественно, различаться.

В экономике Украины модель Альтмана пока не получила широкого применения по следующим причинам:

1. требуется вычисление соответствующих коэффициентов при показателях Ki, i=1,5, которые, естественно, отличаются от их значений для зарубежных стран;
2. информация офинансовом состоянии анализируемых предприятий, как правило, недостоверна, руководство ряда предприятий «сознательно» подправляет свои показатели в финансовых отчетах, что делает невозможным найти достоверные оценки коэффициентов в Z- модели;

Поэтому задача оценки вероятности риска банкротства должна решаться в условиях неопределенности, неполноты исходной информации, и для ее решения предлагается использовать адекватный аппарат принятия решений – нечеткие множества и нечеткие нейронные сети (ННС).

Задается лингвистическая переменная Е «Состояние предприятия», которая имеет пять значений:

E1 – нечеткое подмножество состояний «предельного неблагополучия»;

E2 – нечеткое подмножество состояний «неблагополучия»;

E3 – нечеткое подмножество состояний «среднего уровня»;

E4 – нечеткое подмножество состояний «относительного благополучия»;

E5 – нечеткое подмножество состояний «предельное благополучие».

Соответствующая переменной E лингвистическая переменная G «Риск банкротства» также имеет 5 значений:

G1 – нечеткое подмножество состояний «предельный риск банкротства»;

G2 – нечеткое подмножество состояний «степень риска банкротства высокая»;

G3 – нечеткое подмножество состояний « степень риска банкротства средняя»;

G4 – нечеткое подмножество состояний «низкая степень риска банкротства»;

G5 – нечеткое подмножество состояний «риск банкротства незначительный».

Построим набор отдельных показателей X={Хi} общим числом N, которые по мнению эксперта, с одной стороны влияют на оценку риска банкротства предприятия, а с другой стороны, оценивают разные по природе стороны деловой ифинансовой жизни предприятия. Например, в матричном методе используются такие показатели 

Х1 – коэффициент автономии (отношение собственного капитала к валюте баланса);

Х2 – коэффициент обеспечения оборотных активов собственными средствами (отношение чистого оборотного капитала к оборотным активам);

Х3 – коэффициент промежуточной ликвидности (отношение суммы денежных средств и дебиторской задолженности ккраткосрочным пассивам);

Х4 – коэффициент абсолютной ликвидности (отношение суммы денежных средств к краткосрочным пассивам);

Х5 – оборачиваемость всех активов за год (отношение выручки от реализации к средней выручке за период стоимости активов);

Х6 – рентабельность всего капитала (отношение чистой прибыли к средней за период стоимости активов).

Введем следующие лингвистические переменные для реализации алгоритмов нечеткого вывода Мамдани и Цукамото.

Х1: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий);

Х2: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий);

Х3: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий);

Х4: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий);

Х5: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий);

Х6: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий);

Задаем следующие уровни банкротства: (Очень Низкий, Низкий, Средний, Высокий, Очень Высокий).

Проводим фаззификацию входных параметров, или описание каждого из терм-множеств (лингвистических переменных) с помощью функций принадлежности, и находим степени истинности для каждого значения в правилах: A1(x0), A2(x0), В1(у0), В2(у0)

В качестве функций принадлежности будем использовать треугольные функции. Для большей наглядности функций принадлежности представим их графически на рис.1 и укажем на них соответствующиефактические значения показателей.

Проводится объединение найденных усеченных функций с использованием операции max, что приводитк получению конечного нечеткого подмножества для выходной переменной с функцией принадлежности m(z).

Осуществляется приведение к четкости центроидным методом:

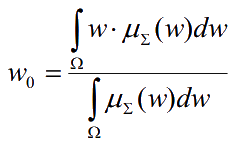
Для анализа разных методов оценки риска банкротства был разработан программный комплекс, в котором реализованы классический метод дискриминантного анализа Альтмана, метод Давыдовой- Беликова, матричный метод Недосекина на основе нечетких множеств и нечеткие нейронные сети (ННС) Мамдани и Цукамото. Используя разработанный программный комплекс, были проведены прогнозирования банкротства для пятидесяти восьми предприятий Украины, 29 из которых в 2011 году арбитражным судом были признанные банкротами.

Выводы

В статье рассмотрены методы прогнозирования риска банкротства предприятий: классические методы дискриминантного анализа Альтмана и нечетко-множественный метод Недосекина.

Проведены экспериментальные исследования указанных методов для прогнозирования риска банкротства предприятий Украины.

Список использованной литературы

1.Давыдова Г.В. Методика количественной оценки риска банкротства предприятий / Давыдова Г.В., Беликов А.Ю. // Управление риском, 1999. – № 3.– с. 13-20.с
2. Зайченко Ю.П. Зайченко Ю.П. Нечеткие модели и методы в интеллектуальных системах. – К.: Видавничий Дім "Слово", 2008. – 352 с.
3. Недосекин А.О. Максимов О.Б. Анализ риска банкротства предприятия. Метод. указания по курсу Антикризисное управление [Електронний ресурс]/ Недосекин А.О. Максимов О.Б., Павлов Г.С. // – Режим доступа к журн.: http://sedok.narod. ru/sc_group.htm.
4. Altman E.I, 1983 Altman E.I. Corporate Financial Distress/ Altman E.I. – New York, John Wiley, 1983. – 192 p
5. Altman E.I., 1968] Altman E.I. Discriminant Analysis and the prediction of Corporate Bankruptcy. / Altman E.I. // Financial Ratios. // Journal of Finance. – 1968. – September. – pp. 589-609.