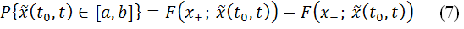Назад в библиотеку
Теоретичні підходи в моделюванні поведінки вкладників
Автор: Тузова О.О., Тарасова О.О.
Источник: Стратегічний розвиток національної економіки, регіонів і підприємств: Т.4. Моделі і методи ефективного стратегічного планування соціально-економічного розвитку; матеріали Всеукраїнської науково-практичної конференції, 15-17 листопада, 2012 року, м. Донецьк. – Донецьк: ДонДУУ, 2012.–221 с.
Розвиток сучасних фінансово-економічних відносин припадає на період глибинних трансформаційних процесів в банківській справі, застосування інновацій в організації і формах обслуговування клієнтів, методах управління банком. Традиційні види банківської діяльності ускладнилися, придбали якісно нові риси, що не мають аналогів в банківській практиці раніше.
Загальнотеоретичні та концептуальні основи банківської справи, функціонування системи банківського менеджменту в умовах конкуренції, що посилюється, знайшли відображення в роботах вітчизняних і зарубіжних вчених: Г. Авагян, О. Амоши, Е. Долана, К. Кэмбела, Ж. Матука, Г. Панової, О. Поважного, П. Роуза, М. Савлук, В. Тинякової, О. Шеремет та ін.
Однак питанням залучення вкладників, моделювання їх поведінки приділено недостатньо уваги, при цьому необхідно зазначити, що в сучасних банківських системах вклади населення є основним джерелом залучення коштів і вимагає від банків високої репутації в очах вкладників. Таким чином, управління процесами залучення грошових ресурсів, що забезпечує як мінімізацію можливих витрат, так і достатність наявних депозитів для фінансування кредитів, які банк бажає надавати своїм клієнтам, є найважливішою характеристикою якості його роботи в цілому [2].
З метою управління процесами залучення коштів необхідно вивчити поведінку вкладників, яке носить імовірнісний характер. Так пропонується розділити вкладників на два типи:
1) реальний вкладник – такий клієнт банку, на рахунку якого до моменту часу t0 лежить внесок величиною x0>0;
2) потенційний вкладник – вкладник, який ще не відкрив свій рахунок до моменту часу t0.
Для кожного типу вкладників розробляються відповідні стохастичні моделі. Так П. В. Конюховський [3] представляє обставини, що тягнуть закриття рахунку реального вкладника, за допомогою дискретної випадкової величини
 , розподіленої за законом Пуассона.
, розподіленої за законом Пуассона.
Тоді ймовірність ліквідації рахунку до моменту часу t визначається формулою:
а ймовірність збереження рахунку до моменту часу t – формулою:
де λ– – параметр інтенсивності пуассонівського процесу.
Сам же випадковий момент часу 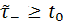 , в який відбувається закриття рахунку, відносять до експоненціально розподіленої випадкової величини.
, в який відбувається закриття рахунку, відносять до експоненціально розподіленої випадкової величини.
Кількість проведених над рахунком операцій без його ліквідації  також розглядає як приріст пуассонівського процесу
також розглядає як приріст пуассонівського процесу  з інтенсивністю λ [3].
з інтенсивністю λ [3].
Введемо випадковий коефіцієнт 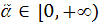 зміни величини вкладу після проведення вкладником однієї операції і передбачається, що він має логарифмічно нормальний розподіл. Тоді дисперсія випадкового коефіцієнта зміни суми депозиту має вигляд:
зміни величини вкладу після проведення вкладником однієї операції і передбачається, що він має логарифмічно нормальний розподіл. Тоді дисперсія випадкового коефіцієнта зміни суми депозиту має вигляд:
Знаючи початкову величину вкладу x0 і випадковий коефіцієнт 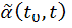 її зміни за проміжок часу [t0,t], можемо визначити величину внеску в момент часу t:
її зміни за проміжок часу [t0,t], можемо визначити величину внеску в момент часу t: 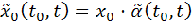 .
.
Для прогнозування величини внеску на момент часу t, можна використовувати математичне сподівання:
Точність такого прогнозу слід оцінювати за допомогою стандартного відхилення 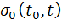 випадкової величини
випадкової величини 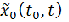 .
.
Розглядаючи поведінку потенційного вкладника, пропонується вводити випадкову величину 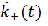 з параметром інтенсивності λ+, яка характеризує обставини, які сприяють відкриттю рахунку в банку.
з параметром інтенсивності λ+, яка характеризує обставини, які сприяють відкриттю рахунку в банку.
Потенційний вкладник має два варіанти прийняття рішення на проміжку часу [t0,t]:
1) відкрити рахунок, з ймовірністю:
2) не відкривати рахунок на момент часу t, з ймовірністю:
Якщо рахунок відкривається у випадковий момент часу 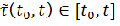 , що має експоненційний розподіл, то стають можливими всі варіанти поведінки вкладника.
, що має експоненційний розподіл, то стають можливими всі варіанти поведінки вкладника.
Щоб врахувати варіант невідкриття рахунку до моменту часу t, потрібно ввести випадковий коефіцієнт:
1)  з ймовірністю p+(t0,t);
з ймовірністю p+(t0,t);
2)  з ймовірністю q+(t0,t).
з ймовірністю q+(t0,t).
Якщо величину вкладу потенційного вкладника на момент часу t задають інтервалом:  , то достовірність такої оцінки визначається з імовірністю:
, то достовірність такої оцінки визначається з імовірністю:
Таким чином, представлені моделі поведінки реальних і потенційних вкладників дають можливість банкам прогнозувати обсяги депозитних коштів, що знаходяться в їх розпорядженні, а отже, оцінювати свої можливості у кредитуванні клієнтів.
Розвиток системи регулювання поведінки вкладників, основною метою якого є захист інтересів вкладників і запобігання банкрутству банків, повинна поєднувати в собі механізм з прозорою системою звітності та інформованості вкладників, яка визначає перспективи для подальшого розвитку банку.
Література:
1. Вишняков И.В. Экономико-математические модели оценки деятельности коммерческих банков. – СПб: СПбГУ, 1999. – 354 с.
2. Искаков М.Б. Модели и методы управления привлечением вкладов в банковскую сберегательную систему. – М.: ИПУ РАН, 2006. – 156 с.
3. Конюховский П.В. Микроэкономическое моделирование банковской деятельности. – СПб: Питер, 2001. – 224 с.: ил.
 , розподіленої за законом Пуассона.
, розподіленої за законом Пуассона.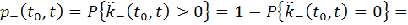
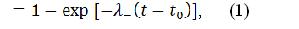

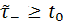 , в який відбувається закриття рахунку, відносять до експоненціально розподіленої випадкової величини.
, в який відбувається закриття рахунку, відносять до експоненціально розподіленої випадкової величини. також розглядає як приріст пуассонівського процесу
також розглядає як приріст пуассонівського процесу  з інтенсивністю λ
з інтенсивністю λ 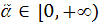 зміни величини вкладу після проведення вкладником однієї операції і передбачається, що він має логарифмічно нормальний розподіл. Тоді дисперсія випадкового коефіцієнта зміни суми депозиту має вигляд:
зміни величини вкладу після проведення вкладником однієї операції і передбачається, що він має логарифмічно нормальний розподіл. Тоді дисперсія випадкового коефіцієнта зміни суми депозиту має вигляд: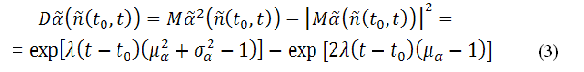
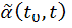 її зміни за проміжок часу [t0,t], можемо визначити величину внеску в момент часу t:
її зміни за проміжок часу [t0,t], можемо визначити величину внеску в момент часу t: 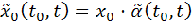 .
.
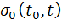 випадкової величини
випадкової величини 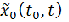 .
.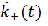 з параметром інтенсивності λ+, яка характеризує обставини, які сприяють відкриттю рахунку в банку.
з параметром інтенсивності λ+, яка характеризує обставини, які сприяють відкриттю рахунку в банку.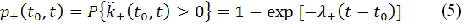
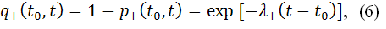
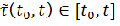 , що має експоненційний розподіл, то стають можливими всі варіанти поведінки вкладника.
, що має експоненційний розподіл, то стають можливими всі варіанти поведінки вкладника.  з ймовірністю p+(t0,t);
з ймовірністю p+(t0,t); з ймовірністю q+(t0,t).
з ймовірністю q+(t0,t). , то достовірність такої оцінки визначається з імовірністю:
, то достовірність такої оцінки визначається з імовірністю: