Вступ

Необхідність аналізу та управління депозитами фізичних осіб викликана високою значимістю цих коштів у складі джерел залучених коштів банку. Випадковий характер процесу залучення, в свою чергу, обумовлює потребу в спостереженні за поведінкою клієнтів і станом їх вкладів протягом усього періоду дії депозитного договору. З плином часу конкуренція вимагає від банків внесення змін до існуючих депозитних програм, та створення абсолютно нових. Впровадження нових продуктів в свою чергу впливає на показники ризику та дохідності банку, тому формування оптимального депозитного портфелю та моніторинг показників за кожним окремим депозитним продуктом є важливими складовими успішності комерційного банку.

Питання, пов'язані з дослідженням теоретичних основ управління депозитним портфелем комерційного банку, сформованої практики реалізації та шляхів вдосконалення депозитної політики в науковій літературі розроблені недостатньо.

Постановка завдання

Метою дослідження є моделювання життєвого циклу депозитного продукту.

Результати

У даній роботі пропонується дослідження строкового депозиту. Нехай T – період строкового вкладу. Під життєвим циклом депозиту будемо розуміти період часу з моменту появи депозиту на ринку й до моменту виведення його з ринку.

Позначимо V_di(t) обсяг коштів, залучених за депозитом d_i, тоді схематично життєвий цикл депозиту може бути представлений у вигляді кривої зростання суми накопичених коштів (рис. 1) [3].

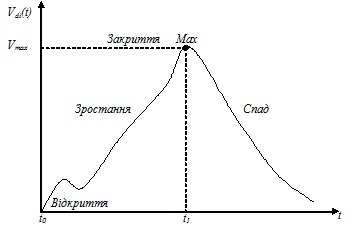
Рисунок 1. Життєвий цикл депозиту.

Динаміку сум коштів, накопичених на рахунках клієнтів можна змоделювати спираючись на теорію стохастичних процесів. Оцінимо кількість клієнтів в кожен момент часу за допомогою розгалужених процесів Гальтона-Ватсона, що представляють собою ланцюг Маркова X(t) на множині невід'ємних цілих чисел з початковим розподілом ймовірностей P₀(k) = P(X(0) = k) та перехідними ймовірностями [1]:

P_kj = P(X(t + 1) = j | X(t) = k,                                                              (1)

де X(t) – кількість клієнтів в момент часу t;

k, j – номери станів у ланцюзі й одночасно кількість клієнтів, які уклали з банком депозитний договір, k, j = 0, 1, 2…;

P_kj – ймовірність переходу в стан j у момент часу (t +1) за умови, що в момент часу t система знаходиться в стані k.

Початковий стан характеризується наступними властивостями:

P₀(1) = P(X(0) = 1, P₀(k) = 0                                                              (2)

для всіх k ≠ 1, що означає, що в початковий момент часу кількість клієнтів Z(0), з якими було укладено депозитний договір, дорівнює одиниці.

Розіб'ємо загальний строк депозиту Т на кілька періодів моделювання – N, довжина одного періоду може скласти день, тиждень, місяць і т. д.

Оскільки після закінчення обраного періоду моделювання клієнт може або продовжити депозитний договір X(t + 1) = 1 | X(t) = 1, або розірвати його з імовірністю відмінною від нуля X(t + 1) = 0 | X(t) = 0, то загальна кількість вкладників буде постійно зменшуватися. Такі процеси відносяться до класу докритичних, для них ймовірність виродження дорівнює 1.

Виникає необхідність залучення клієнтів ззовні. Процес укладання контрактів з новими клієнтами може бути описаний як процес імміграції. Тоді кількість контрактів за даним депозитним продуктом виражається наступним чином:

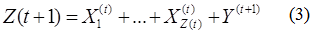
де X^(t)_l – кількість договорів l-го клієнту в момент часу t;

Y^(t+1)– кількість клієнтів, що прийшли в банк в момент часу t + 1.

Якщо сума коштів на рахунку клієнта – випадкова величина, то загальна накопичена сума коштів по депозиту в момент часу t може бути описана як сума всіх вкладень по цьому депозиту до моменту часу t:

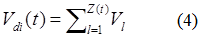
де V_l – сума коштів на рахунку l-го клієнту.

Випадкова величина V_di(t) описується складовим законом розподілу. Для його визначення необхідно задати розподільні закони величин V_l та Z(t). У свою чергу для знаходження розподілу Z(t) потрібні закони розподілу випадкових величин X^(t)_l й Y^(t+1), що входять до неї.

Для чисельних обчислень скористаємося твірними функціями ймовірностей, які задають закони розподілів вхідних параметрів.

Висновки.

Таким чином, розроблена математична модель життєвого циклу депозиту дозволяє отримати закони розподілу обсягів залучених коштів V_di(t) у кожний з модельованих моментів часу, що дозволяють визначити значення суми акумульованих коштів та ймовірність їх залучення.

Література:

1.Ватутин В.А. Лекционные курсы НОЦ / Математический институт им. В.А. Стеклова РАН (МИАН). М.: МИАН, 2008. Вып. 8: Ветвящиеся процессы и их применения / - 108 с.
2. Димаков С.А. Разработка механизма управления пассивами коммерческого банка // Траспортное дело России. 2008. №4. – С. 61-64.
3. Шолохова Н.В. Подходы к управлению депозитным портфелем коммерческого банка // Вестник УГАТУ. Т. 16, №8 (53). – Уфа: УГАТУ, 2012. – С. 183-189.