Моделирование колебаний груза при перемещении тележки мостового крана
Автор: С.Р. Бежин, А.И. Хиценко
Источник: Машинознавство/ Матеріали 13 регіональної науково-методичної конференції. Донецьк, ДонНТУ. – С. 55-59.
Аннотация
С.Р. Бежин, А.И. Хиценко. Моделирование колебаний груза при перемещении тележки мостового крана. В данной работе разработана и реализована математическая модель движения тележки мостового крана с грузом в системе Mathcad. Получены графики колебаний груза в вертикальной и горизонтальной плоскотях, график изменения угла поворота груза..
При работе мостового крана происходит постоянное чередование направления движения крана, тележки и крюка. Одной из актуальных задач является оптимизация режимов работы грузовой тележки с целью уменьшить динамические нагрузки на механизм перемещения тележки и избежать колебаний груза, закрепленного на гибком подвесе.
Вопросы оптимизации режимов движения крановых механизмов рассматриваются в работах таких ученых как В.С. Ловейкин, В.Ф. Ярошенко, В.П. Балашов, Н.А. Лобов, Б.В. Квартальнов, В.И. Ключев, Ю.А. Борцов, Б.Ш. Бургин, В.Н. Тищенко, Г.Г. Соколовский, Р.П. Герасимяк, И.Я. Браславский и др. В работе [1] поставлена и решена задача выбора оптимальных законов движения крановой тележки, при которых колебания исчезали на протяжении переходных режимов ее движения и которые не приводили бы к значительным нагрузкам на конструкцию. Недостатком данной работы является не учет параметров груза (положения центра тяжести и момента инерции).
Целью работы является оценка колебаний груза при движении тележки с учетом его параметров, а также упругих и инерционных характеристик конструкции мостового крана.
Для исследования движения грузоподъемного механизма была составлена трех массовая динамическая модель (рис. 1).
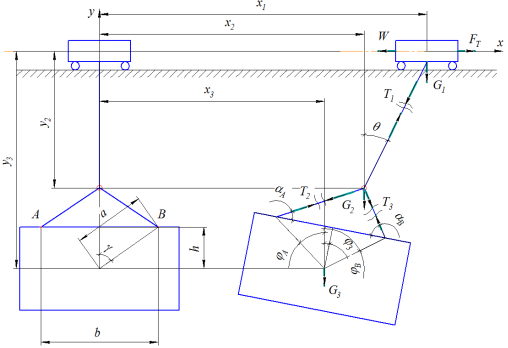
Рисунок 1 - Расчетная динамичная модель движения грузоподъемного механизма мостового крана
На рисунке 1: m1 – масса грузоподъемной тележки; FТ – суммарное тяговое усилие; W – сила сопротивления движению тележки; T1 – сила натяжения каната; T2, T3 –силы натяжения строп; G1 – сила тяжести грузоподъемной тележки; G2 – сила тяжести крюка; G3 – сила тяжести груза; φ3 – угол поворота груза; αА, αВ – угол между грузом и стропой; θ – угол отклонения каната от начального положения; h – расстояние по вертикали между центром тяжести груза и местом закрепления строп; b – расстояния межу местами закрепления строп; a – расстояние между центром тяжести груза и местом закрепления строп.
Используя уравнения движения твердого тела [2], составлена система дифференциальных уравнений:
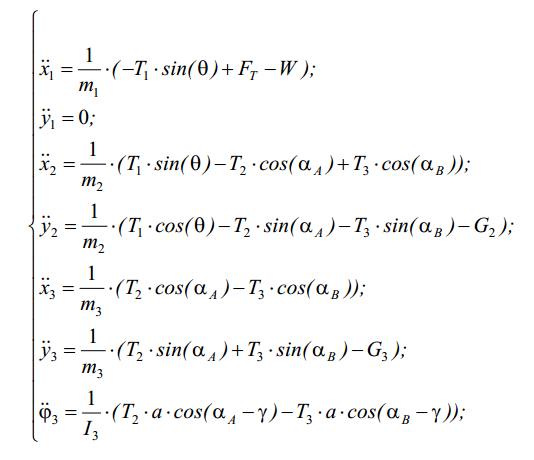
где 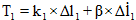 - сила натяжения каната;
- сила натяжения каната;
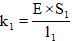 - коэффициент жесткости каната;
- коэффициент жесткости каната;
Е - модуль упругости материала каната;
 - площадь сечения каната;
- площадь сечения каната;
d1 - диаметр каната;
c - коэффициент заполнения сечения каната;
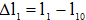 - удлинение каната;
- удлинение каната;
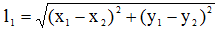 - длина каната во время движения;
- длина каната во время движения;
l10 - длина каната в положении равновесия;
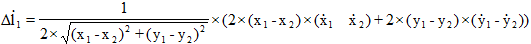 - скорость удлинения каната;
- скорость удлинения каната;
β - коэффициент рассеивания энергии;
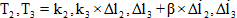 - сила натяжения строп;
- сила натяжения строп;
 - коэффициент жесткости строп;
- коэффициент жесткости строп;
 - площадь сечения строп;
- площадь сечения строп;
Е - модуль упругости материала строп;
d2, d3 - диаметр строп;
с - коэффициент заполнения сечения строп;
 - удлинение строп;
- удлинение строп;
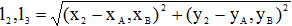 - длина строп во время движения;
- длина строп во время движения;
l20, l30 - длина строп в положении равновесия;
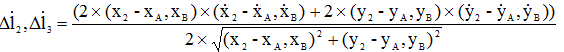 - скорость удлинения строп;
- скорость удлинения строп;
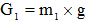 - сила тяжести тележки;
- сила тяжести тележки;
m1 - масса тележки;
g - ускорение свободного падения;
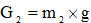 - сила тяжести крюка;
- сила тяжести крюка;
m2 - масса крюка;
 - сила тяжести груза;
- сила тяжести груза;
m3 - масса груза;
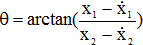 - угол отклонения каната от начального положения;
- угол отклонения каната от начального положения;
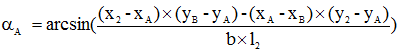 - угол между грузом и стропой;
- угол между грузом и стропой;
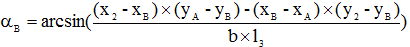 - угол между грузом и стропой;
- угол между грузом и стропой;
h - расстояние по вертикали между центром тяжести груза и местом закрепления строп;
b - расстояния межу местами закрепления строп;
Разработанная математическая модель была реализована в виде расчетного листа Mathcad. Система дифференциальных уравнений была решена численным методом Рунге-Кутта 4-го порядка, заложенным во встроенную функцию rkfixed().
Примером работы программы являются графики колебаний груза в
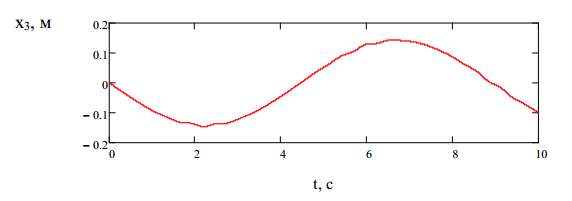
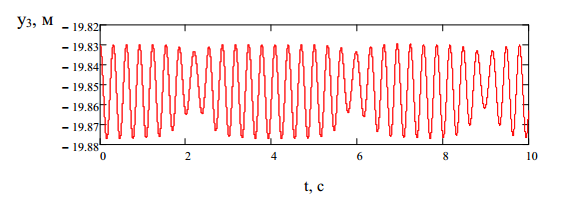
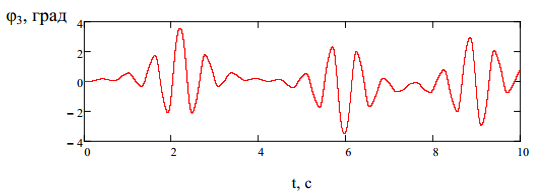
горизонтальной плоскости (рис. 2), колебаний груза в вертикальной плоскости (рис. 3), угла поворота груза (рис. 4) при скорости движения тележки
0,1 м/с для таких исходных данных: m1=500 кг, m2=20 кг, m3=1000 кг, l10 =15 м, l20 = l30 =5 м, d1 =0,01 м, d2 =d3=0,005 м, Е =1,0·1011 Па [3], с =0.76, h =0.5 м, b=5 м, I3 =3.5 кг*м2.
Рисунок 2 - График колебаний груза в горизонтальной плоскости Рисунок 3 – График колебаний груза в вертикальной плоскости Рисунок 4 – График изменения угла поворота груза Таким образом, разработана и реализована в системе Mathcad математическая модель движения тележки мостового крана с грузом. Разработанная программа позволяет рассчитывать законы движения груза и тележки. С использованием данной программы в дальнейшем будет осуществлен выбор оптимальных режимов движения тележки, учитывающих скорость движения и параметры груза. 1. Ловейкин В. С., Ярошенко В.Ф. Оптимизация переходных режимов движения механизма передвижения тележки грузо-
подъемных машин // Вестник Харьковского национального технического университета сельского хозяйства. -2007-№59, том 2. – С. 452-460.
2. Яблонский А. А. Курс теоретической механики. Часть II. Динамика. – Москва: «Высшая школа», 1984. – 567 с.
3. Малиновский В.А. Стальные канаты. Часть 1. Некоторые вопросы технологии, расчета и проектирования. –Одесса: Астропринт, 2001. – 188 с.
Список использованной литературы