Адаптивная система управления механизмами передвижения мостовых кранов.
Автор: J. Szpytko, J. Smoczek and D. Lakomski
Автор перевода: С.Р. Бежин
Источник: Adaptive control system of overhead crane's movement mechanismes/ International Carpathian Control Conference ICCC’ 2002
Аннотация
J. Szpytko, J. Smoczek and D. Lakomski. Адаптивная система управления механизмами передвижения мостовых кранов. В статье представлена система управления мостового крана на основе нечеткой логики множеств.
Введение
Мостовые краны в автоматизированных системах производства должны иметь высокуюточность движений с уровнем безопасности, надежности и эксплуатационных расходов приемлемых пользователем (Szpyko et al. 2000a). В поисках новых решений в области надлежащего контроля движения механизмов, которые должны быть компромисс между сопротивлением и адаптации с переменной нагрузкой системы.
По экономическим причинам в старых систем привода были использованы трехфазных асинхронных двигатели. Развитие преобразователей обусловило то, что в настоящее время двигатели с короткозамкнутым ротором используются чаще (или гибридные системы - асинхронный двигатель и инвертор, особенно в мостовые краны).
Проблема мостового крана главным образом касается решений в области контроля одного из механизмов передвижения (наиболее часто это тележка движения) в аспекте минимуму колебание нагрузки подвешенного на канате (Auerning et al. 1987, Chi-Cheng et al., Manhfouf et al. 2000). Есть несколько статей ориентированых на интеграцию тележки, мост и подъемного механизма (Al.-Garni et al. 1995, Szpytko et al. 2000b).
Системы управления тележка движении с поднятым грузом с использованием линеаризации и контроллера в замкнутом контуре была представлен в публикации (Chi-Cheng et al. 1996). Предметом исследования (Grega et al. 2001) является описание реальных объектов и архитектуры прототипов оборудования. в исследования авторы представили программно-аппаратную среду для алгоритма управления прототипами. Эта система была выполненна с возможностью управления упрощенной мостовой кран лаборатории.
1. Модель системы управления механизма мостового крана
Для исследования механизма движения мостового крана была построена трехмассовая модель как электромеханическое устройство(масса: тележки M1, моста м2), которое транспортирует груз м3 подвешенный на канате (рис. 1).
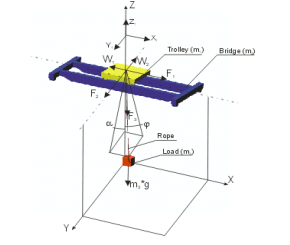
Рисунок 1 – Модель мостового крана
Математическая модель мостового крана была описана в исследовании (Szpytko et al. 2001).
Для устранения нежелательных эффектов, сопровождающих эксплуатацию устройства (превышение нагрузке и кручение моста) система управления на основе нечеткой логики.
Система управления мостового крана состоит из шести контроллеров типа Sugeno-TakagiKanga (STK) (Yager et al. 1995), обозначиных как FLC1 – FLC 6.
Функции принадлежности треугольного типа были использованы в процессе создания логики множеств. Для входных сигналов были назначены лингвистические термины N (отрицательный), Z (ноль) и P (положительная).
Система управления моста движение представлена на рисунке 2. Задача FLC1 это назначение скорости моста на основе информации об ошибки о расположении позиции моста. Контроллер FLC2 – на основе информации об ошибках скорости и направления моста.Система корректирует крутящий момент между левой и правой позиции моста изменяя сигнал U, который управляет скоростью колес моста.
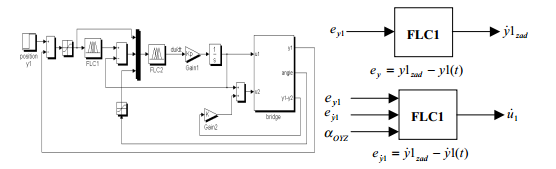
Рисунок 2 – Схема системы управления движением моста и макета ввода/вывода сигналов
Контроллеры и FLC3 FLC4 STK типа управляют движением тележки (рис. 3).

Рисунок 3 – Схема системы управления движением тележки и макета ввода/вывода сигналов
Контроллеры и FLC5 FLC6 STK типа управляют механизмом подъема (рис. 4).

Рисунок 4 – Схема системы управления движением механизма подъема
2. Исследование системы управления движением механизма
Моделирования были проведены в среде Matlab/Simulink для параметров реального мостового крана грузоподъемностью 12500 кг.
Предполагалось,что Целью контроль было расположить груз оптимальным образом в декартовом пространстве от отправной точки до конечной точки в рабочем пространстве, с минимальными колебание груза и кручением моста. Результаты были представлены в работах (Szpyko et al. 2001, Szpytko et al. 2002). Характеристики полученые во время моделирования были представлены в рисунках 5 и 6.
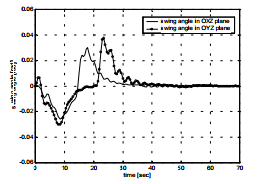
Рисунок 5 – Характеристика изменения угла положения груза в областях OXZ и OYZ.
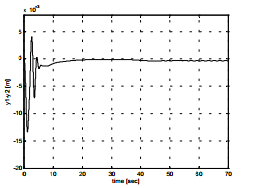
Рисунок 6 – Характеристика изменения положения колес крана
Нечеткой системы управления на основе нечеткокой логики множеств позволяет достичь малого угла отклонения груза от заданной траектории(0,03 ? 0035 [рад]) в течение кран движения. Окончательное положение сдвинутого груза была достигнута с заданной точностью в OXYX пространстве для предполагаемой траектории движения.
Также в ходе опыта были получены характеристики вращения моста (рис. 7) и реальной силы для преодоления сил сопротивления движению (рис. 8). Опыт проводился на ненагруженом устройстве, с номинальной скоростью и управлением человеком оператором.
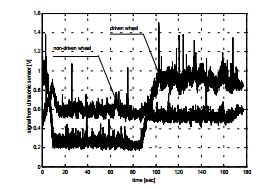
Рисунок 7 – Характеристика вращения моста
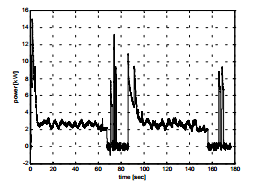
Рисунок 8 – Характеристика силы, преодолевающей силы сопротивления движению
Исследования, проведенные на модели мостового крана и на реальном объекте позволяют констатировать, что: – качественные изменения характеристик выбранного устройства и виртуальной модели совместимы; – разработана модель системы управления краном позволяют изучать и искать оптимальную стратегии управления грузом в рабочей области. Результатов, достигнутых в модели виртуального мостовой кран и исследований проведеных на реальном объекте подтверждают возможность минимизации нежелательного эффектов путем формирования характеристики запуска и торможения механизма. Предложенная система управления позволяет минимизировать кручение, при котором является невозможным осуществить управления скоростью моста.
Выводы
Исследования, проведенные на виртуальнуой модели крана, позволяют утверждать, что использование нечеткой логики множеств в системе управления мостового крана может быть выгодно для его эксплуатации. Это подтверждается результатами, достигнутыми в области минимизации раскачивания груза и размещению груза по предполагаемой траектории движения. Предлагаемая система управления позволяет формировать характеристики крутящего момента, минимизируя перегрузки в переходных режимах, достигая ровных характеристик угловых скоростей двигателя.
Дальнейших исследований с использованием интеллектуальных методов управления мостовыми кранами будет проводиться в направлении реализации разработаной системы управления на реальном объекте. Успешное выполнение этой цели возможно при использовании преобразователей частоты приводов и аппаратной платформы, реализующей алгоритм нечеткого управления. Аппаратная архитектура состоит из компьютера PC и многозадачных телег. Для проектирования и достижения целей планируется применить тележки производства фирмы PLC компании Advantech 818HG PLC и 726, которые позволяют обеспечить быстрое прототипирования в среде Matlab.
Список использованной литературы
1. AL.-GARNI A.Z., MOUSTAFA K.A.F., NIZAMI J.S.S.A.K. 1995: Optimal Control of
Overhead Cranes. Control. Engineering Practice, 1995, v. 3, no. 9, pp. 1277-1284.
2. AUERNIG J.W., TROGER H. 1987: Time Optimal Control of Overhead Cranes with
Hoisting of the Load. Automatica, 1987, v. 23, no. 4, pp. 437-447.
3. BENHIDJEB A., GISSINGER G.L. 1995: Fuzzy Control of an Overhead Crane
Performance Comparison with Classic Control. Control Engineering Practice, 1995, v.
3, no. 12, pp. 1687-1696.
4. CHI-CHENG CHENG, CHENG-YI CHEN 1996: Controller for an overhead crane system
with uncertainty. Control Engeenering Practice, 1996, v. 4, no. 5, pp. 645-653.
5. GREGA W., PAULUK M., TURNAU A. 2001: Projektowanie algorytmow sterowania dla
suwnicy ramowej. ZN Polit. Opolskiej, Opole 2001, z. 64, no. 265, pp. 129-136.
6. MAHFOUF M., KEE C.H., ABBOD M.F., LINKENS D.A. 2000: Fuzzy Logic-Based AntiSway Control Design for Overhead Cranes. Neural Computating and Applications, 9,
2000, pp. 38-43.
7. MENDEZ J.A., ACOSTA L., MORENO L., TORRES S., MARICHAL G.N. 1999: An
Application of a Neural Self Controller to an Overhead Crane. Neural Computing and
Applications, 8, 1999, pp. 143-150.
8. MORENO L., MENDEZ J.A., ACOSTA L., TORRES S., HAMILTON A., MARICHAL
G.N. 1998: A self-tuning neuromorphic controller: application to the crane problem.
Control Engineering Practice, 6, 1998, pp. 1475-1483.
9. ROSENFELD Y. 1995: Automation of existing cranes: from concept to prototype.
Automation in Construction, 1995, no. 4, pp. 125-138.
10. SZPYTKO J., DRZYMALA Z., WASILEWSKI A. 2000a: Wybrane zagadnienia
optymalizacji eksploatacji suwnic. Miedzynarodowa Konferencja NaukowoTechniczna: Napedy Maszyn Transportowych, Ustron Slaski 2000, no. 4, pp. 59-64.
11. SZPYTKO J., SMOCZEK J., CHODACKI J. 2000b: Badanie wplywu operatora na
przebieg rozruchu mechanizmow suwnic pomostowych. Miedzynarodowa
Konferencja: Napedy Maszyn Transportowych, Ustron Slaski 2000, no. 4, pp. 54-58.
12. SZPYTKO J., SMOCZEK J., LAKOMSKI D. 2001: Investigation of intelligent fuzzy based
control system of overhead crane. Pre-prints of the 16th IFAC Workshop on
Intelligent Manufacturing Systems, IFAC IMS’01, 2001, pp. 140-145.
13. SZPYTKO J., SMOCZEK J., WOJTOWICZ E. 2002: Transportation processes
automation in flexible manufacturing systems. Machine Engineering, v. 2, no. 1-2,
2002, pp. 223-231.
14. YAGER R.R., FILEV D.P. 1995: Podstawy modelowania i sterowania rozmytego. WNT,
Warszawa 1995.