Оптимизация переходных режимов движения механизма передвижения крановой тележки
Автор: Хиценко Н. В. , Бежин С. Р.
Источник: Подъемно-транспортное оборудование и логистика/ Материалы 2 региональной студенческой научно-технической конференции. Донецк. ДонНТУ. - С. 81-83.
Аннотация
Хиценко Н. В. , Бежин С. Р. Оптимизация переходных режимов движения механизма передвижения крановой тележки. В данной статье получен закон управления механизмом перемещения тележки. Исследовано влияние длительности разгона и торможения на максимальное отклонение груза от вертикали при различных значениях длины отвеса и массы груза.
При работе крана происходит постоянное чередование направления движения крана, тележки и крюка. Так, работа механизма подъема состоит из процессов подъема и опускания груза и процессов подъема и опускания пустого крюка. Использование оптимальных режимов работы грузовой тележки позволяет: уменьшить динамические нагрузки на механизм перемещения тележки, обеспечивая отсутствие ударов; избежать колебаний груза, закрепленного на гибком подвесе [1].
Качество многих технологических процессов зависит от перемещения грузов подъемно-транспортными машинами. Вопросы оптимизации режимов движения крановых механизмов рассматриваются в работах таких ученых как В.С. Ловейкин, В.Д. Ярошенко, В.П. Балашов, Н.А. Лобов, Б.В. Квартальнов, В.И. Ключев, Ю.А. Борцов, Б.Ш. Бургин, В.Н. Тищенко, Г.Г. Соколовский, Л.Б. Масандилов, Р.П. Герасимяк, И.Я. Браславский и др.
Целью работы является устранение колебаний груза за счет формирования оптимальных переходных режимов движения механизма передвижения крановой тележки та разработка системы, которая обеспечит желательное управляющее воздействие на механизм подъема.
Для исследования движения грузоподъемного механизма была составлена трехмассовая динамическая схема (рис. 1). Соответствующая математическая модель была разработана в статье [2].
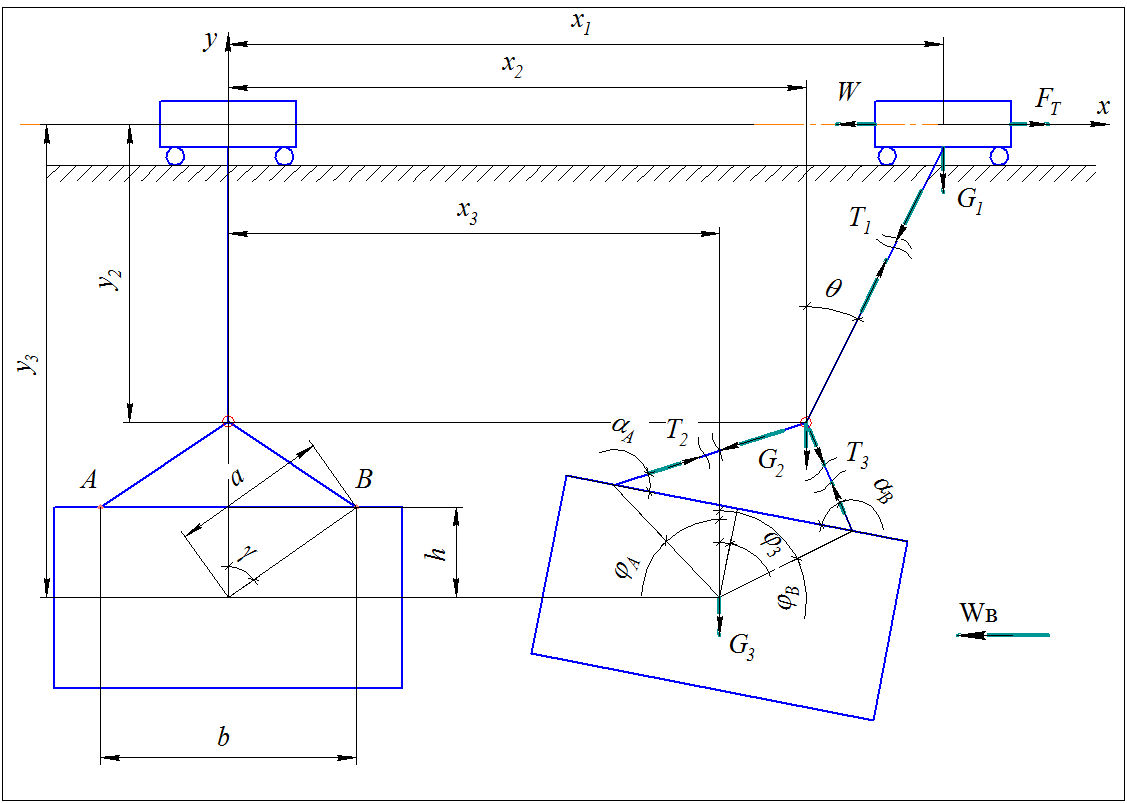
Рисунок 1 - Расчетная динамичная схема движения грузоподъемного механизма.
Для проведения оптимизации переходных режимов движения крановой тележки с грузом был использован закон управления механизмом перемещения тележки, в соответствии с которыми скорость движения тележки задается по формулам:
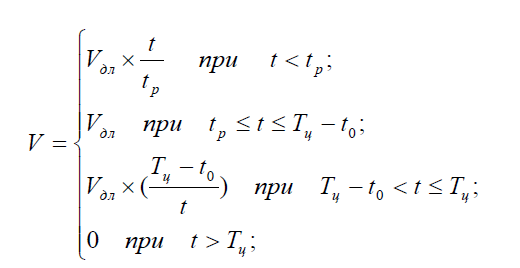
где V – скорость движения тележки, м/с
Vдл - длительная скорость, м/с
t – текущее время перемещения тележки, с
tр - время разгона, с
tо - время останова, с
Тц - время перемещения тележки, с.
В этом законе вся длина пути крановой тележки разбита на 3 участка: участок разгона tp, участок равномерного движения тележки Tц, участок торможения to (Рис. 2).
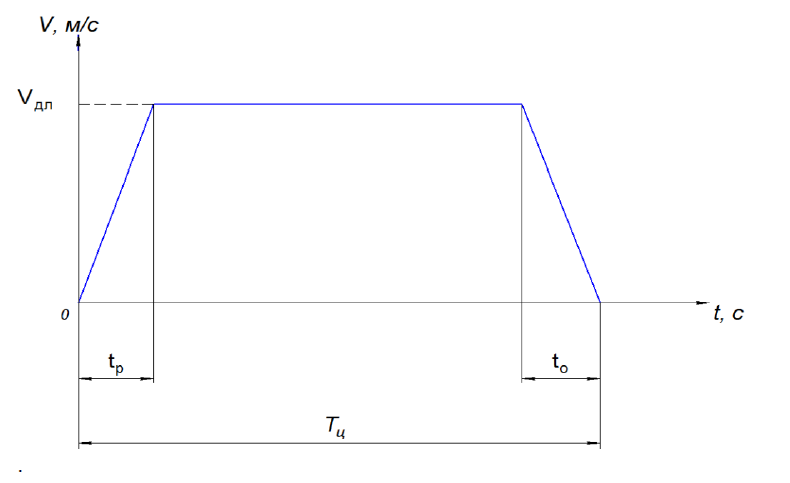
Рисунок 2 – Трапецеидальная тахограмма перемещения тележки.
Для трапецеидальной тахограммы движения тележки исследовано влияние длительности разгона и торможения на максимальное отклонение груза от вертикали при различных значениях длины отвеса и массы груза (рис. 3).
В ходе исследования установлено, что при изменение tр от 1 секунды до 5 секунд приводит к снижению отклонения от 0,4 – 1 м до 0,3 -0,6 м. При массах груза 2,5 – 10 т зависимости практически не изменяются (рис. 3 а, б). Для легких грузов (1 т) отклонения существенно больше до 0,25 - 1 м особенно при большом отвесе (рис. 3 в). Это требует учета массы груза при выборе алгоритма управления приводом передвижения тележки. В дальнейшем планируется исследовать колебания груза при более сложных тахограммах движения.
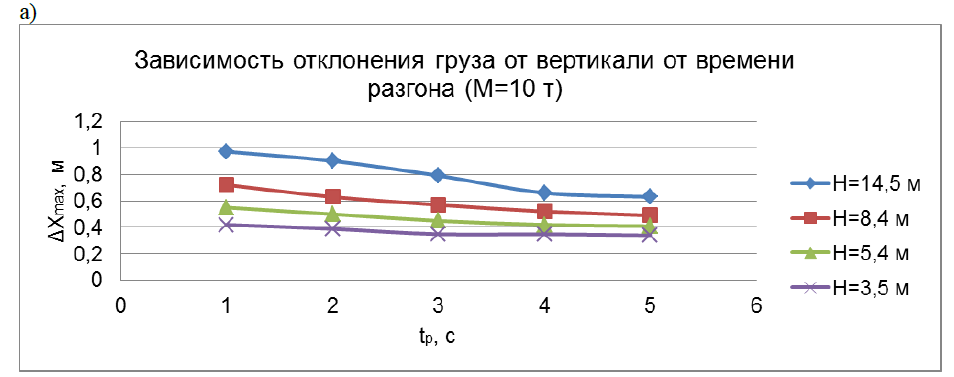
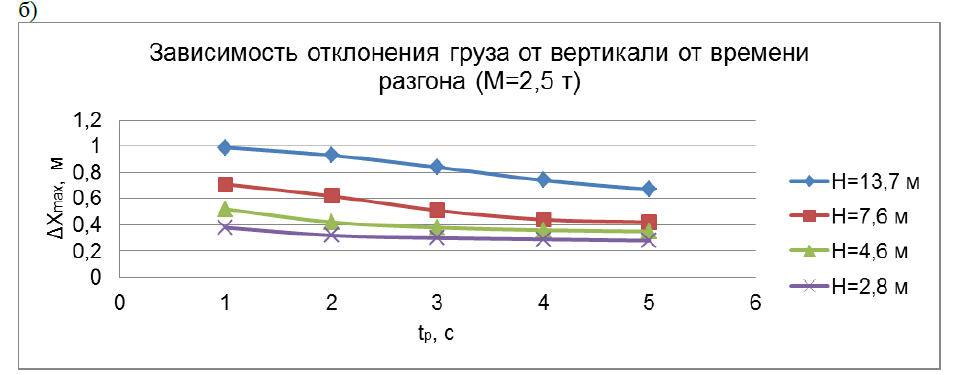
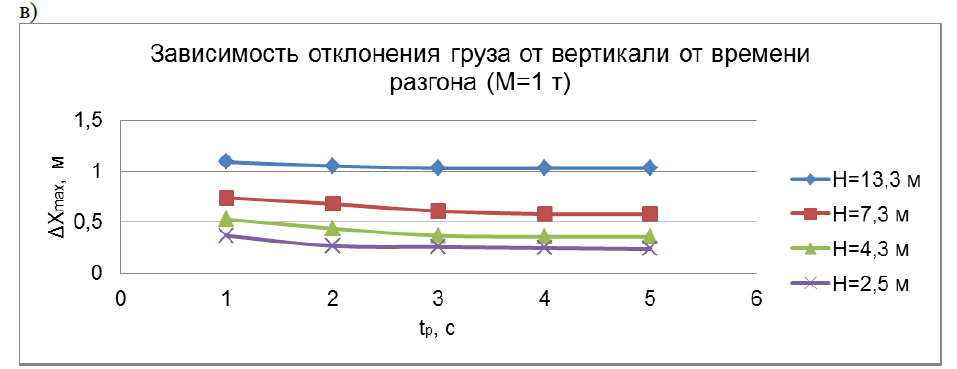
Рисунок 3 а, б, в - Зависимость отклонения груза от времени разгона.
Список использованной литературы
1. Ловейкин В. С. , Ярошенко В.Ф. Оптимизация переходных режимов движения механизма передвижения тележки грузоподъемных машин. Вестник Харьковского национального технического университета сельского хозяйства. -2007-№59, том 2. – С. 452-460.
2. Хиценко А. И. , Бежин С. Р. «Моделирование колебаний груза при перемещении тележки мостового крана» /Машинознавство/ матеріали 13 регіональної науково-методичної конференції. Донецьк, ДонНТУ. – С. 55-59.