Анализ методов оптимизациипереходных процессов в подъемных машинах
Автор: А.П. Нестеров, В.С. Ловейкин, А.А. Пилипенко
Источник: Восточно-Европейский журнал передовых технологий (выпуск 17). Харьков, 2005.
Аннотация
А.П. Нестеров, В.С. Ловейкин, А.А. Пилипенко. Анализ методов оптимизациипереходных процессов в подъемных машинах. Проведенный анализ методов оптимизации шахтных подъемных машин.
Подъемные машины (рис.1) работают в режиме повторно - кратковременного включения механизмов, который характеризуется частыми пусками и остановками. Переходные процессы оказывают существенное влияние на технико–эксплуатационные показатели работы подъемных машин. Оптимизация переходных процессов подъемных машин позволяет повысить их производительность и надежность, а также уменьшить утомляемость оператора и повысить безопасность эксплуатации.
повысить безопасность эксплуатации. В подъемных машинах рассматриваются силовые и режимные процессы. К силовым процессам относятся внешние возмущения, а также стационарные установившиеся и неустановившиеся (колебательные нагрузки, действующие в главной линии передач подъемной машины. Режимные процессы подъемных машин представляют собой характер изменения скорости, ускорения, рывка, скорости нарастания ускорения и т.д. подъемной кабины или других элементов машины, а также параметры, которые определяют режимный процесс: продолжительности цикла движения и переходных участков, максимальные значения скорости, ускорения, рывка и т.д.). На рис.1 показана схема измерений ряда параметров и подъемной машины.
Впервые задача оптимизации силовых и режимных параметров подъемных машин была поставлена М.М.Федоровым [1], а задача оптимизации силовых нестационарных процессов А.Н. Голубенцовым [2]. В работе [3] поставлена задача многокритериального оптимального проектирования подъемных установок в пространстве параметров, как оптимизация силовых процессов в главной линии передач, включающей в себя электродвигатель, редуктор, орган навивки, головные канаты, подъемные сосуды, хвостовые канаты и направляющие шкивы подъемной установки при ограничениях типа неравенства.
В работе [1], рассмотрена задача оптимизации постоянных, изменяющихся по ступенчатому закону внешних возмущений двигателя М (рис.2) для трехпериодной диаграммы скорости (рис.3) по критерию «минимум эффективной мощности привода» без ограничений на режимные параметры.
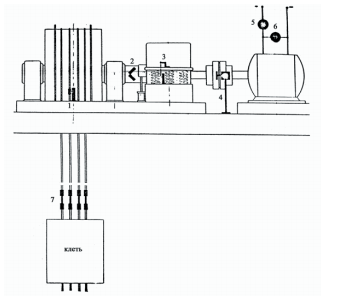
Рисунок 1 – Схема расположения измерительной аппаратуры при экспериментальном исследовании многоканатной установки: 1 – фотодиодный отметчик пути; 2 – тензодатчик для измерения упругого момента на выходном валу редуктора; 3 – реохорд для измерения перемещений корпуса редуктора; 4 – тахогенератор; 5 – амперметр; 6 – вольтметр; 7 – накладные динамометры для измерения усилий в канатах.
В дальнейшем аналогичную задачу в различных вариантах с ограничениями типа равенств и без ограничений рассмотрено другими авторами, в частности [4-8].

Рисунок 2 – Постоянные внешние возмущения М, приложенные на участках пуска (М1), установившегося движения (М2) и торможения (М3) продолжительностью соответственно t1,t2 и t3
Задачу оптимизации эффективной мощности по одно- му параметру при любом законе изменения внешних воз- мущений впервые рассмотрел Давыдов Б.Л. [6]. Он решил ее без ограничений и с ограничениями типа равенств на ускорение и замедление на отдельных участках диаграм- мы скорости (рис 3.) по перегрузке электродвигателя.
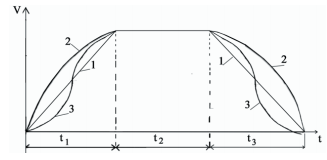
Рисунок 3 – Возможные диаграммы изменения скорости V(t) подъемной машины на участках переходных процессов: 1 – прямолинейная; 2 – параболическая; 3 – по кривой высших порядков
Федоров М.М. пришел к выводу, что минимальной эффективной мощности электродвигателя при постоянных внешних возмущениях соответствует равнобокая трапецеидальная диаграмма скорости, если не наложены ограничения на ускорение и замедление. В работе [9] показало, что при отсутствии ограничений на величину и закон изменения внешних возмущений, оптимальной диаграммой скорости будет параболическая трапеция. Аналогичный результат получен в работе [10] при минимизации интегрального функционала, который представляет собой динамическую составляющую эффективной мощности привода. М.М.Федоров рассмотрел задачу оптимизации силовых параметров барабанных подъемных установок с заданной производительностью и высотой подъема при ступенчатых внешних для трехпериодной диаграммы скорости и ограничениях на режимные параметры (ускорение и замедление) типа равенств [1]. Задача оптимизации силовых параметров подъемной установки в постановке М.М. Федорова решается существенными допущениями, поскольку записывая ограничения для ускорения и замедления в форме равенств, в действительности для любых установок эти параметры принимаются одинаковыми.
В работах [3,11] поставлена и решена задача оптимизации внешних возмущений для заданной подъемной установки в пространстве трех режимных параметров – скорости, ускорения и замедления по критериям «минимум удельных приведенных затрат» и «минимум времени цикла с учетом технических и экономических ограничений типа неравенств. Эта задача решалась поисковыми методами математического программирования.
Задача выбора оптимальной грузоподъемности клетки составляет основу оптимального проектирования подъемных установок. Эту задачу можно сформулировать следующим образом: из всего ряда стандартного оборудования подъемных машин выбрать для подъемной установки с заданной высотой подъема и производительностью такое оборудование, которое отвечает минимальным удельным приведенным затратам на тонну поднимаемого груза или минимальному времени цикла при технических и экономических ограничениях типа неравенств. Эти задачи решались многими авторами в упрощенной постановке, в частности [12,13]. Общее решение задачи оптимального проектирования из-за своей сложности и громоздкости может быть получено методами математического программирования с использованием численных методов и ЭВМ
В ряде случаев в подъемных машинах используются ступенчатые внешние возмущения, которые соответствуют их максимальному быстродействию [14]. В тоже время внешние силы такого типа вызывают значительные колебательные процессы в главной линии передач подъемных машин (Рис.4) [15,16]. Поэтому, возникает задача гашения динамических нагрузок в валопроводе и канатопроводе подъемной машины во время прохождения силовых нестационарных процессов.
Одним из путей решения этой задачи является подбор оптимальных, инерционных и диссипативных параметров линии передач.
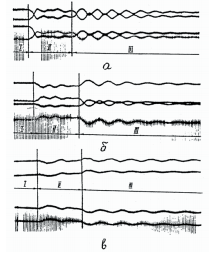
Рисунок 4 – Осциллограмма усилий в нижних сечениях четырех головных канатов одной ветви при аварийном торможении клети (?t = 0,1с): а – в верхней части ствола; б – в средине ствола; в – в нижней части ствола; I –период равномерного движения машины; II – период замедленного движения машины; III – период свободных колебаний канатов при застопоренном шкиве трения.
В качестве средств гашения колебаний используются различные муфты, упруго - демпфирующие вставки, дина- мические, гасители и поглотители энергии [17].
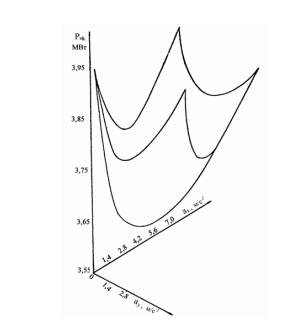
Рисунок 5 – Поверхность отклика функционала цели ”эффективная мощность” в пространстве режимных параметров ускорение и замедление.
Ряд исследователей, например [10,14,16] решают задачу уменьшения механических колебаний в линии передач подъемных машин за счет оптимального управления электроприводом путем использования различных «сглаженных» диаграмм скорости. Однако не всегда этот метод приводит к желательным результатам. Так, например, асинхронные двигатели, управляемые ступенчато, вызывают колебания в механической части линии передач вовремя пуска [18]. Поэтому необходимо выбирать такие средства управления электродвигателем, которые бы обеспечивали плавное управление изменения движу- щего момента при изменении частоты вращения. Наилучшие результаты такого управления достигаются при использовании тиристорной системы управления [19]. При использовании ступенчатого управления электродвигателем необходимо увеличить количество ступеней регулирования, чтобы максимально уменьшить скачок изменения движущего момента. Такая система управления электродвигателем не устраняет полностью колебаний в механической части линии передач во время пуска, однако существенно их уменьшает.
Экстренное торможение механическими тормозами также сопровождается интенсивными колебаниями как в валопроводе, так и в канатопроводе во всех типах подъемных машин [20]. Поэтому в любой подъемной машине всегда имеют место колебательные процессы в линии передач, от которых необходимо избавляться. Достичь желаемого результата в этом направлении можно путем выбора оптимальных режимов движения подъемных машин, которые реализуются плавным управлением изменения движущего и тормозного момента привода и введением в линию передач гасителей колебаний и упруго - демпфирующих звеньев.
Задачу минимизации динамических нагрузок в валопроводе подъемной машины во время прохождения переходных процессов за счет оптимизации жесткостных и инерционных параметров поставки А.Н. Голубенцев в следующем виде: «Выбрать параметры машины: жесткости соединительных элементов и моменты инерции маховых масс такими, чтобы при заданных внешних нагрузках величина дополнительного момента, вызванного упругими свойствами машины, была наименее возможной [2]. В этой работе диссипативные силы не учитывались. Здесь поставленная оптимизационная задача решена аналитически при использовании критерия качества переходного процесса коэффициента динамичности для простейших трехмассовых динамических моделей с двумя упругими звеньями [21]. Дальнейшее увеличение числа упругих звеньев и дискретных масс приводит к тому, что указанную задачу можно решать только численными методами с использованием ЭВМ.
В работе [21] разработан общий метод оптимизации силовых переходных процессов по быстроте затухания колебаний в линии передач шахтных подъемных машин как многомассовых механических систем с упругими звеньями. Для многомассовых механических систем шахтных подъемных машин в работах [3,17,22] и других рассматриваемая задача решалась в общей постановке численно методами математического программирования и находились необходимые и достаточные условия оптимальности переходных процессов по быстроте затухания колебаний в пространстве жесткостных, инерционных и диссипативных параметров.
Специфика работы и конструкций шахтных подъемных машин требует разработки специальных методов и средств исследования и оптимизации силовых переходных процессов и режимов движения приводных механизмов. Экспериментально установлено [23], что в шахтных подъемных машинах имеет место установившейся силовой процесс в период равномерно-ускоренного, равномерного и равномерно-замедленного движения, что обусловлено приложением к двигателю, органу навивки и к подъемным грузам постоянных внешних сил и моментов. В работах [2,11,15,21] показано, что силовой, стационарный поток в упругих звеньях линии передач различного типа машин при заданных постоянных внешних возмущениях зависит от масс и моментов инерции дискретных тел. Однако при переходе с одного установившегося силового процесса к другому установившемуся силовому процессу в элементах силовых передач возникают колебательные процессы [15,16], которые приводят к появлению переменных во времени дополнительных нагрузок. Эти нагрузки способствуют быстрому усталостному изнашиванию конструкций шахтных подъемных машин и, как следствие, преждевременному выходу их из эксплуатации.
В работе [11] впервые выдвинута идея, поставлена и решена задача оптимизации стационарного упругого состояния звеньев шахтной подъемной машины за счет изменения соотношения моментов инерции дискретных масс в линии передач, то есть оптимизации силового стационарного процесса в пространстве инерционных параметров
В работе [16] ставится и решается задача минимизации динамических нагрузок в линии передач при переходе от одного стационарного силового процесса к другому для различных подъемных машин с упругими звеньями. Минимизация силовых переходных и стационарных процессов позволяет создать динамически совершенную шахтную подъемную машину, способную интенсивно выполнять операции подъема груза при постоянных внешних возмущениях. В связи с этим возникает необходимость оптимизации силовых стационарных и переходных процессов каждой конкретной шахтной подъемной установки при заданной высоте подъема. Вся сложность задачи оптимального проектирования подъемной установки заключается в том, что необходимо определить ее оптимальные грузоподъемность, режимы движения и их параметры по заданной проектом высоте подъема и производительности подъемной установки. Одним из путей решения поставленной задачи является определение оптимальной производительности всего ряда типовых шахтных машин при различных высотах подъема с последующей математической обработкой полученных результатов. Целью такой обработки результатов является построение эмпирической зависимости оптимальной грузоподъемности установки как функции ее производительности и высоты подъема [3,11].
Как правило, оптимальная грузоподъемность шахтной подъемной установки, полученная по эмпирическим зависимостям, не совпадает с типовой грузоподъемностью подъемных сосудов. В связи с этим возникает следующая оптимизационная задача: определить типовую шахтную подъемную установку с грузовыми и режимными параметрами, отвечающую минимуму удельных приведенных затрат или минимуму времени цикла при ограничениях на затраты, а также минимуму эффективной мощности привода. Указанная экстремальная дискретно - континуальная задача решается методами математического программирования и реализуется в виде пакета прикладных программ для ЭВМ.
Проведенный анализ методов оптимизации в теории шахтного подъема показывает, что поиск наилучших решений при оптимизации грузовых, режимных и конструктивных динамических параметров подъемных машин проводится по одному критерию и с изменением одного параметра. Поэтому ставится задача совместного исследования и комплексной оптимизации силовых переходных процессов и внешних возмущений в шахтных подъемных машинах по нескольким критериям в пространстве параметров.
В процессе оптимизации переходных процессов шахтных подъемных машин центральное место занимает выбор критерия оценки силового или режимного переходного процесса
Для каждого переходного процесса могут быть выделены наиболее характерные критерии качества, которые в полной мере характеризуют тот или иной процесс. По этим критериям может проводится оптимальный синтез шахтных подъемных машин. Оптимальным силовым процессам ставятся в соответствие оптимальные режимы движения и конструктивные параметры подъемной машины. Под оптимальными силовыми процессами подъемных машин будем понимать такие процессы, которым соответствует экстремальное (минимальное или максимальное) значение некоторого критерия, представленного в виде функционала (функции, зависящей от функции).
Нестационарные силовые процессы в главной линии передач шахтной подъемной машины могут быть оценены несколькими показателями: темпом затухания колебаний - критерии «обобщенный декремент колебаний» и «быстрота затухания колебаний»; максимальной амплитудой колебаний – критерии «коэффициент динамичности» и « максимальное отклонение»; степенью приближения колебательного процесса к желаемому процессу – критерии «интегральное квадратичное отклонение» и «абсолютное максимальное отклонение»; длительностью затухания колебаний – критерий «время затуханий колебаний»; степенью влияния на работоспособность различных узлов - критерии «потеря усталостной прочности» и «снижение долговечности»; затратами механических средств – критерии в виде «действия» [8,24,25].
Анализ проведенных исследований с помощью приведенных критериев показывает, что последние достигают минимальных значений внутри или на границе области допустимых значений варьируемых параметров [8,11,17].
От закона изменения внешних воздействий, действующих на главную линию передач со стороны электродвигателя, зависит стоимость электро-оборудования и потребляемой электроэнергии, время цикла работы шахтной подъемной машины и др. и, в конечном итоге, производительность, надежность и экономичность подъемной установки
Внешние возмущения оцениваются несколькими показателями качествами: стоимостью одной тонны поднимаемого груза – критерий «удельные приведенные затраты»; продолжительностью работы подъемной установки – критерий «времени цикла»; величиной эффективной мощности привода – критерий «эффективная мощность»; темпом затухания колебаний – критерий «быстрота затуханий»; максимальной амплитудой колебаний – критерий «коэффициент динамичности»; затратами механических средств – критерии в виде «действия» и др.
При установлении закона изменения внешних воздействий априори принимается, что любой современный электропривод может реализовать такие управления шахтной подъемной машины, которые обеспечивают во времени t диаграмму скорости V(t) в виде криволинейной трапеции (см.рис.3). При этом боковые стороны этой трапеции могут быть представлены прямыми линиями -1, параболами-2 или кривыми более высоких порядков – 3. В свою очередь, одному из указанных законов изменения скорости в виде прямо-линейной трапеции соответствуют постоянные, приложенные ступенчато внешние возмущения (см.рис.2), удовлетворяющие при ограничениях на режимные параметры условию максимального быстродействия шахтной подъемной машины по управлению [14].
Реализуемость такого типа возмущений определяется, в первую очередь, возможностью уменьшения колебательности силового переходного процесса в звеньях линии передач за счет подбора оптимальных динамических параметров (жесткостных, инерционных и диссипативных), отвечающих минимуму коэффициенту динамичности и максимальной быстроте затухания колебаний.
Синтез оптимальных динамических, силовых и режимных параметров шахтных подъемных машин сводится к отысканию глобального экстремума соответствующего критерия качества (функционала цели) как функции одной, двух или нескольких переменных с учетом ограничений на функционалы и параметры в виде равенств или неравенств. В простейших случаях, когда удается получить аналитическое выражение функционала цели в виде функции нескольких переменных без ограничений, исследования его на экстремум возможно методами математического анализа. Этими методами миними-зируются функционалы цели для частных случаев: «удельные приведенные затраты», «эффективная мощность», ряд критериев типа «действия».
Шахтные подъемные машины представляют собой многомассовые механические системы, эквивалентные динамические модели которых могут состоять из 6-15 дискретных масс, соединенных между собой 5-14 упругими звеньями, обладающими упруго-вязкими свойствами.
Оптимизационный динамический синтез таких систем в пространстве жесткостных, инерционных и диссипативных параметров невозможен без применения численных методов и ЭВМ.
Задача оптимизации силовых переходных процессов шахтных подъемных машин в пространстве и параметров является многопараметри-ческой, нелинейной задачей математического программирования, так как функционалы цели и функции ограничений в общем случае являются нелинейными относительно варьируемых параметров. На функционалы и параметры наложены ограничения в виде неравенств.
В отличие от задач линейного программирования задачи нелинейного программирования не имеют общего метода решения, а существующие частные методы включают в себя элементы экспериментирования. Для решения таких оптимизационных задач шахтных подъемных машин могу быть эффективно использованы известные поисковые методы нелинейной оптимизации, основанные на вычислении и сравнении значений функций в ряде точек перед последующим шагом вычислений [26].
Для параметрической оптимизации могут быть использованы градиентные овражные методы с использованием идеи случайного поиска, так как поверхности отклика функционалов цели силовых переходных процессов шахтных подъемных машин в общем случае носят много- экстремальный характер
При помощи рассматриваемого метода произведена оптимизация режимных параметров: ускорения а1 и замедления а3 в процессах пуска и торможения по критерию «эффективная мощность Pэф = f (а1,а3). На рис.5 показана поверхность отклика функционала цели Pэф = f (а1,а3) для заданной подъемной установки при ограничениях на указанные параметры. Из этого рисунка видно, что поверхность отклика имеет вид чаши с глобальным минимумом, а на границе области допустимых параметров имеются и локальные экстремумы/
Для многоканатной подъемной установки со скипами полезной грузоподъемностью 25т., высотой подъема 95м и суточной производительностью 11000 т/сутки численными методами математического программирования найдены следующие оптимальные параметры: 1) с учетом ограничений: min Pэф=3750кВт; opt а1= opt а3 = =1,2 м/с2 ; 2) без учета ограничений: min Pэф=3643кВт; opt а1= opt а3 = =2,06 м/с2 ;
В практике проектирования возможны случаи, когда значения минимума min Pэф = f (а1,а3) лежат внутри области ограничений параметров а1,а3. Для этих случаев можно найти аналитическое выражение эффективной мощности как функции одной переменной - номинальной скорости подъема Vн.
Аналогичным образом проводится оптимизация режимных параметров и по другим критериям качества переходных процессов шахтных подъемных машин.
Выводы
Проведенный анализ методов оптимизации шахтных подъемных машин показывает, что на протяжении последних нескольких десятков лет проводятся исследования по совершенствования силовых переходных процессов, которые направлены на выбор конструктивных, динамических и режимных параметров, а в ряде случаев и режимов движения приводных механизмов. Использование этих методов оптимизации позволило значительно уменьшить динамические нагрузки колебательного характера в элементах валопроводов и канатопроводов и на их основе со- вершенствовать существующие и создавать новые высокоэффективные и надежные шахтные подъемные машины.
Список использованной литературы
1. Федоров М.М. Избранные труды в 2-х т.-к.: Издательство
АН УССР,1957.-Т.1.С.192-217.-1960.-Т.2.-с.167-17.
2. Голубенцев А.Н. Динамика переходных процессов в машинах
со многими массами.-М.:Мосгиз, 1996. -146с.
3. Научные основы рационального проектирования и
эксплуатации элементов подъемного оборудования (Под
ред.Нестерова П.П. -К.: Наукова думка,1997.-204с.
4. Севастеев В.Г. Теория, построения и расчет оптимальных
автоматических электроприводов рудничного подъема.-
Диссертация докторских технических наук.-М.,1966.-366с.
5. Чермалых В.М. Исследование оптимальных по динамичности
систем подъема глубоких шахт.- Диссертация докторских
технических наук.- Днепропетровск,1970.-420с.
6. Давыдов Б.Л. Вариационные методы теории рудничного
подъема. –В кн,: Рудничный подъем.-М.: Металлургиздат,
1953.-С.315-350.
7. Динкель А.Д. Метод расчета оптимальных параметров режима
работы рудничной скиповой подъемной установки / физико-
технические проблемы разработки полезных ископаемых:
Научно-техническая статья., 1972.- №3.-С.3-43.
8. Горский Б.Е., Ловейкин В.С. Применение коэффициентов
удельных действий при исследовании подъемных
механизмов // Горн., строит. и дор. маш.: Респ. Межвед.
научн.-техн.ст.-190. Вып.29.-С.67-73.
9. Левин Б.Я., Браиловский С.Б. к вопросу о наивыгоднейшим
динамическом режиме рудничного подъема. – В.кн.:
Рудничный подъем.- М.:Металлургиздат, 1953.-С.306-314.
10. Ловейкин В.С. Определение оптимальных режимов
движения механизмов в грузоподъемных машинах //
Подъемно транспортное оборудование:- Респ. Межвед.
Научн.-техн.сб.-1987. – Вып.18.- С.31-35.
11.Нестеров А.П. Принципы оптимального проектирования
шахтных подъемных установок// Респ. Межвед. Научн.-
техн.сб.-1982.-Вып.13. – С.40-42.
12. Нестеров А.П., Бредихин Ю.Р. О допустимых ускорениях
шахтных подъемных машинах.-В.кн.: Теория горных машин
и рабочих процессов.-К.: Наукова думка, 1977.-С.113-117.
13. Проектирование и эксплуатация подъемных комплексов
железнорудных шахт/ Ю.Г.Киричек, В.В.Ройзен,
Н.И.Илиенко и др.-М.: Недра, 1992.-232с.
14. Григоров О.В., Ловейкин В.С. Оптимальне керування рухом
механізмів вантажопідйомних машин.- К.: ІЗМН,1997.-264с
15. Кожевников С.Н. Динамика нестационарніх процессов в
машинах.-К.: Наукова думка, 196.-2с.
16. Ловейкін В.С. Мінімізація динамічних навантажень в
пружних елементах вантажопідйомних машин // Гірничі, 63
будівельні, дорожні та меліоративні машини: Респ. Міжвід.
Наук.- техн.зб.-1998.- Вип.52.-С.63-68.
17. Колосов А.В., НестеровА.П. Оптимизация параметров
нелинейных муфт шахтных подъемных машин //
Подъемн.-трансп.оборуд.:Респ.межвед. научн.-техн. сб.
– 1977. –Вып.8.-С.24-27.
18. Хализев Ю.В. Асинхронные электродвигатели.-М.:
Энергия,1975.-96с.
19. Динкель А.Д., Католиков В.Е., Петренко В.И., Коваль Л.М.,
Тиристорный электропривод рудничного подъема.- М.:
Недра, 1977.-312с.
20. Белобров В.И. Динамика, нагрев и износ тормозов шахтных
подъемных машин.-К.: Наукова думка, 1981.-199с.
21. Голубенцев А.Н. Интегральные методы в динамике. – К.:
Техніка, 1967.-350с.
22. Теория и практика подъема /Л.А.Алексеева, Ю.Р. Бридихин,
Л.А. Волобуев и др..- К.: Наукова думка,1975.-357с.
23. Найденко И.С., Белый В.Д. Шахтные многоканатные
подъемные установки.-М.: Недра, 1979.-390с.
24. Горский Б.Е. Динамическое совершенствование
механических систем.-К.: Техніка,1987.-200с.
25. Ловейкін В.С. Критерії оцінки нажимів руху механізмів і
машин// зб.наук. праць Національного аграрного універ-
ситету.-К.: НАУ.-Т.IV, 1998.-С.8-12.
26. Дегтярев Ю.И. Методы оптимизации. – М.: Советское
радио,1980.-272с.