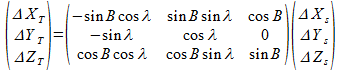
Название: Объединение наземных геодезических сетей и спутниковых построений
Авторы: И.А. Клыпин
Описание: Рассматривается задача объединения наземных и спутниковых геодезических сетей. Приводится вариант алгоритма объединения, основанный на формулах рекуррентного уравнивания.
Источник: Известия высших учебных заведений. Геодезия и аэрофотосъёмка, № 5, 2011 с. 30 – 31.
Объединение наземных геодезических сетей и спутниковых построений
Аннотация. Рассматривается задача объединения наземных и спутниковых геодезических сетей. Приводится вариант алгоритма объединения, основанный на формулах рекуррентного уравнивания.
Ключевые слова: геодезические сети, спутниковые построения, уравнительные вычисления
В настоящее время при строительстве, кадастровых работах, топографических съёмках или
при выполнении геодезических изысканий во многих случаях имеет место совместное использование наземных и спутниковых геодезических построений. Возникает задача объединения и совместного уравнивания этих сетей.
В большинстве предлагаемых алгоритмов уравнивание выполняется в пространственной
геоцентрической системе координат, в которой выполняются спутниковые определения и в которую редуцируются наземные измерения и координаты наземных опорных точек. Теоретически это бесспорно правильно, но на практике далеко не всегда осуществимо и целесообразно. Прежде всего, потому что в этом случае необходимо, чтобы исходные наземные пункты имели координаты, привязанные к некоторому референц-эллипсоиду, и должны быть точные параметры перехода к референц-эллипсоиду, относительно которого определены координаты спутниковых наблюдений. В условиях построения локальных сетей обеспечение этих требований трудно выполнимо: имеются некоторые ограничения в доступе к полным координатам, а используемые системы координат (СК-42, СК-63) не имеют точных параметров перехода в систему WGS-84 [1].
В таком случае весьма перспективным, на наш взгляд, использование при совместном уравнивании наземных и спутниковых построений метода, который успешно применяется при уравнивании сетей аналитической фототриангуляции [2]. Суть метода заключается в том, что проекции векторов спутниковых определений из геоцентрической системы координат перевычисляются в топоцентрическую по следующей формуле:
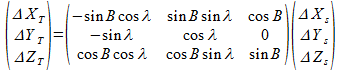
где B и λ – долгота и широта средней точки сети на эллипсоиде, в которой устанавливается топоцентрическая система координат. Далее, переходя от проекций к координатам, можно записать следующие уравнения связи для нашего случая (исходя из всем известных формул преобразования координат):
![]()
во многом аналогичные тем, что возникают при совместном уравнивании плановых построений [3], но с матрицей
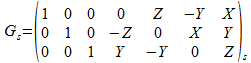
Для реализации способа условий с дополнительными неизвестными формируется матрица
перехода
![]()
после введения которой составляется матрица обратных весов
![]()
Затем согласно [4] получаем корреляционную матрицу

и далее, учитывая по рекуррентным формулам каждое из условных уравнений
![]()
отдельно для каждой из осей координат и выполняя контроль грубых ошибок, в результате
будем иметь уравненные векторы координат S,T и вектор параметров преобразования координат a .
Используя уравненные значения параметров преобразования, теперь нужно лишь перевести
вектор координат S в систему координат T. При этом их подвекторы, относящиеся к идентичным пунктам, в идеале должны совпасть, что будет являться контролем поставленной задачи.
Остаётся только, найдя матрицу обратных весов вектора уравненных величин и определив
квадратичную форму, произвести оценку точности полученных результатов согласно всем
известной формуле теории математической обработки геодезических измерений.
Ввиду определённой нелинейности задачи относительно вектора a и некоторой приближённости вектора координат пунктов, полученных из спутниковых наблюдений может возникнуть задача уточнения матрицы G. Как правило, данная проблема решается путём повторного уравнивания [5, 6]. Но и его можно исключить, если на этапе определения приближённых значений параметров преобразования определять также приближённые
координаты пунктов сетей по методу сопряжённых градиентов [7], применение которого значительно экономит процессорное время на выполнение операций по сравнению с повторным уравниванием, а также повышает устойчивость вычислительного процесса.
Экспериментально данный алгоритм был реализован в программной среде MathCAD. К его достоинствам можно отнести значительно меньшие по сравнению с аналогичными алгоритмами требования к оперативной памяти компьютера, особенно при работе с обширными сетями, а также возможность включения в обработку новых данных без переуравнивания всей сети. Кроме того, следует иметь в виду, что согласно описанному алгоритму производится строгое уравнивание геодезических построений.
ЛИТЕРАТУРА
1. Могильный С. Г. Совместная обработка наземных и спутниковых геодезических измерений в локальных сетях/ С.Г. Могильный, А.А. Шоломицкий / Сучасні досягнення геодезичної науки і виробництва. Зб. наук. праць. — Львів: Львівська політехніка. — 2009. — Вип. 1 (17) — С. 122–131.
2. Grenzdoerffer G. Konzeption, Entwicklung und Erprobung eines digitalen integrierten flugzeuggetragenen Fernerkundungssystems fuer Precision Forming (PFIFF). DGK, Muenchen, 2002. Reihe C, Heft Nr. 552. — 141 s.
3. Клыпин И. А. К вопросу об уравнивании геодезических сетей, построенных в разных системах координат. // Изв. вузов.≪Геодезия и аэрофотосъёмка≫. 2010. — №6. — С. 11–13.
4. Маркузе Ю. И. Основы метода наименьших квадратов и уравнительных вычислений: Учебное пособие. — М.:МИИГАиК, 2005. — 288 с.
5. Маркузе Ю. И., Вельш В. М. Два алгоритма объединения наземных и спутниковых сетей // Изв. вузов ≪Геодезия и аэрофотосъемка≫. — 1995. — №2. — С. 45–64.
6. Маркузе Ю. И., Антипов А. В. Возможности улучшения алгоритма объединения спутниковых и наземных сетей //Геодезия и картография. — 2004. — №4. —С. 16–21.
7. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. — М.: Наука. — 1963. — 656 c.