А.Н. Макарова, А.А. Лакиза Обоснование подхода к решинею задачи прогноза малоамплитудных нарушений

На сегодняшний день актуальным вопросом является проблема отработки запасов угля на шахтах Украины. Добыча угля осложняется такими факторами как большая глубина разработки, высокий уровень горного давления, слоистость массива, трещиноватость, водообильность, высокая газоносность пластов. Наиболее проблемным фактором при отработке пластов , является малоамплитудная нарушенность. Сложность в том, что до ведения очистных работ нарушения с маленькой амплитудой практически невозможно обнаружить [3] . Расстояния между разведочными скважинами достигает сотен метров следовательно уловить нарушение амплитудой 0,3-1,5 м практически невозможно. В связи с этим применяют ряд геофизических методов, которые производят непосредственную разведку малоамплитудных нарушений. Однако такие методы требуют значительных затрат для закупки специального оборудования. Трудоемкость обработки промежуточных данных при проведении работ значительна .кроме того восстановление параметров нарушений и их координат является задачей, которая не имеет однозначного решения. К тому же надежность результата доразведки как правило не более 80%.

В связи с этим целесообразным является разработка новых менее трудоемких и доступных методов решения данной проблемы. Эффективным является привлечение методов искусственного интеллекта, для расчета и прогнозирования малоамплитудной нарушенности в массиве [2] . Для их применения необходимо иметь достоверные данные об уже вскрытых нарушениях. На основании полученных данных мы имеем возможность создать эвристическую модель. Затем эту модель тренируют по вышеуказанным данным до тех пор пока она сможет обобщить скрытые закономерности распределения малоамплитудной нарушенности.

Например при панельном способе отработки и ярусной подготовке лав обратным ходом, обязательно проводятся два вентиляционных штрека, монтажная печь. По указанным выработкам мы получаем ряд необходимых данных, фиксируя все встреченные малоамплитудные нарушения. Показания используются для определения параметров нарушения внутри выемочного столба.

На рисунке 1 показан план горных выработок. На данном фрагменте наглядно видно, как часто могут встречаться в массиве малоамплитудные нарушения.

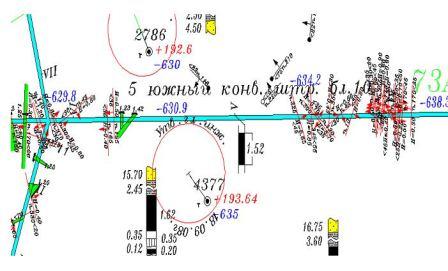
Рис. 1 Фрагмент плана горных выработок М 1:5000

Расстояния между нарушениями от 70 до 500 метров, амплитуда от 0,25 до 0,5 метров. угол падения изменяется в интервале от 35° до 50°. видно что нарушения распределены неравномерно, следовательно предсказать их местоположение и параметры очень сложно. Наблюдая за характером появления нарушений можно сделать предварительный вывод о том, что чередуемость параметров появления нарушений вдоль линии 5 южного конвейкрного штрека , может быть представлена простой информационной моделью. Чередуемость соседних малоамплитудных нарушений можно представить как , потоки событий которые не происходят в один промежуток времени [1]

В связи с этим будет проведена апробация нового подхода для расчета зон появления малоамплитудных нарушений. Авторами данной статьи сделано предположение о том что , предсказать характер нарушений можно используя марковские процессы[1]. Марковский процесс – это случайный процесс эволюция которого после любого заданного значения временно́го параметра t не зависит от эволюции, предшествовующего t, при условии, что значение процесса в этот момент фиксировано .

Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений, достаточную популярность марковские процессы получили у специалистов занимающихся исследованием операций и теорией принятия оптимальных решений.

Рассмотрим модель , которую в любой момент времени можно описать одним из N состояний, где для простоты N = 5.

Через определенный промежуток времени модель может изменить свое состояние или остаться в прежнем состоянии согласно вероятностям, указанным для данных состояний. Моменты времени, когда мы регистрируем состояние модели, обозначим как t = 1,2 , а состояние в момент времени t обозначим qt. Полное описание модели должно содержать текущее состояние (в момент времени t) и последовательность всех предыдущих состояний, через которые прошла система. В отдельных случаях описание модели сводится к указанию текущего и предыдущего состояния, то есть

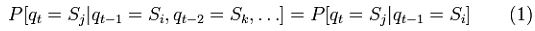
Кроме того, мы также полагаем что процессы, протекающие в системе, не зависят от времени, о чем нам говорит правая часть формулы (1). Таким образом, систему можно описать множеством вероятностей aij в виде

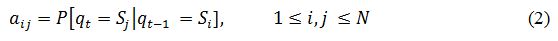
где aij — это вероятность перехода из состояния Si в состояние Sj в данный момент времени. Поскольку эти вероятности характеризуют случайный процесс, они имеют обычные свойства, то есть

Описанный случайный процесс можно назвать открытой марковской моделью, поскольку выходной сигнал модели — это последовательность состояний, регистрируемых во времени. Каждое состояние соответствует определённому (наблюдаемому) событию. В нашем случае роль времени выполняет координата вдоль линии вдоль которой регистрируют нарушения. А в качестве событий выступает факт реализации конкретного расстояния между соседними малоамплитудными нарушениями.

Дальнейшими исследованиями является предварительное обоснование и проработка методики анализа вскрытых параметров фактически установленных малоамплитудных нарушений.

Литература

Тихонов В.И., Миронов М.А. «Марковские процессы» , - М,1977
Назимко В.В., Мерзликин А.В. Опыт применения нейронных сетей и генетического алгоритма для прогноза малоамплитудных нарушений Научные труды Донецкого Государственного Технического Университета. Серия: горно-геологическая. – 2002. – №54. –С. 177 – 183.
Назимко В.В., Захаров В.С. , Мерзликин А.В. Прогноз мелкоамплитудных разрывных нарушений угольных пластов с помощью нейронных сетей и генетических алгоритмов Геотехнологии на рубеже 21 в.,т.2. – Донецк.: ДонНТУ, 2001. - С. 30-32