Особенности распределения стохастических отклонений оседаний земной поверхности при её подработке одиночной лавой
Авторы:Бугаёва Н.А., Назимко В.В.
(ДонНТУ, г.Донецк, Украина)
Авторы:Бугаёва Н.А., Назимко В.В.
(ДонНТУ, г.Донецк, Украина)
Угольная промышленность является энергетической основой Украины, что обусловливает необходимость ее развития. Повышение интенсивности добычи угля и производительности очистных работ является главным требованием, которое предъявляет рыночная экономика к угольной промышленности нашей страны. Именно поэтому объемы добычи угля ежегодно возрастают и в ближайшей перспективе должны достичь 100 млн. тонн в год.
Подземная разработка месторождений полезных ископаемых сопровождается сдвижением массива горных пород и земной поверхности. Это вызвано опусканием толщи пород под силами тяжести в пустоты выработанного пространства. В итоге оседания толщи достигают земной поверхности, которые негативно влияют на сохранность искусственных и природных объектов, существовавших на земной поверхности до ведения очистных работ, либо возведенных после подработки поверхности
Процесс сдвижения в осадочных толщах происходит, как правило, за пределом упругости. При этом влияние выемки угля на состояние земной поверхности отмечается даже при глубине разработки 1000 м и более. В процессе предсказания и оценки нарушенности земной поверхности присутствует некая неопределенность. В связи с этим возникают существенные погрешности при расчете параметров мульды сдвижений. Поэтому прогноз ожидаемых показателей сдвижений продолжает оставаться весьма актуальной задачей в связи с рядом нерешенных проблем.
Одна из таких проблем связана с тем, что фактические распределения показателей сдвижений земной поверхности при ее подработке существенно отличаются от расчетных, которые определяются по стандартным методикам. К сожалению, большинство существующих методик рассматривают процесс сдвижения как детерминированный.
Так основные нормативные документы, применяемые в настоящее время в отечественной и зарубежной практике [1-4] для расчета ожидаемых оседаний и деформаций земной поверхности при ее подработке длинными очистными забоями определяют однозначное положение мульды и детерминированное значение параметров деформации в пространстве и не дают возможности установить диапазоны вероятного их разброса. Вместе с тем анализ известных на сегодня публикаций в отечественной и зарубежной литературе свидетельствует о существенных отклонениях фактически измеренных оседаний от расчетных. При этом отклонения носят случайных характер и не связаны с повреждениями наблюдательных станций или систематическими погрешностями. Несовпадение расчетных и измеренных показателей деформации земной поверхности носит не только количественный но и качественный характер. Так на участках, где согласно теории прогнозируется горизонтальное сжатие, наблюдаются растяжения, а вогнутость меняется на выпуклость земной поверхности, затронутой очистными работами. На рис. 1 показаны оседания земной поверхности по одной из угольных шахт Чехии. Данные результаты взяты из сборника научных работ [2]. Рассматривается подрабатываемая площадь размерами 300*1000 м. Авторы публикации [2] описывают результаты инструментальных измерений и расчетов мульды оседаний сформированной на земной поверхности при отработке угольного пласта №40 Prokop двумя лавами 40501 и 40502, одна из которых отрабатывалась прямым ходом, а вторая обратным. Управление кровлей осуществлялась путем полной закладки выработанного пространства золоуносом электростанции. Месторождение отрабатывалось в густо населенном промышленном районе. Отсюда возникает актуальная задача предохранения зданий и сооружений от опасных деформаций и недопустимых оседаний.
Длина лав составляет около 300 м. Глубина разработки составляла около 500 м. Средний угол падения пласта составляет 15°. Мощность пласта 3,5 м, однако так как применяется полная закладка выработанного пространства, оседания имеют меньшую амплитуду. Полная закладка выработанного пространства снижает оседания в 2 и более раз.
Рис. 1 отображает измеренные и расчитанные различными методами оседания земной поверхности вдоль профильной линии. Методы 2, 3, 4 предложены авторами статьи [2] и являются экспериментальными. Первый метод является нормативным, поэтому измеренная линия оседаний сравнивается с линией полученной с помощью этого метода. Анализируя график, можно сделать вывод о том, что оседание над лавой в пределах проекции выработанного пространства изменяется в диапазоне 1,5-2,7 м, в то время как оседания расчитанные по нормативному методу составляют 1,5-1,9 м. Видно, что расчитанная мульда оседаний имеет плавные формы и практически симметрична относительно центра сплошного выработанного пространства. В противоположность измеренная в натурных условиях мульда имеет резкие изменения значений оседаний и явно несимметрична. Так на реперах №12, 16, 18, 20, 22 наблюдается перепад в виде уступа, хотя вероятность регистрации такого вида деформаций при отработке месторождения пологого залегания весьма мала, поскольку в пределах влияния подработки нарушения отсутствовали. Видно, что измеренная мульда оседаний несимметрична относительно центра лавы. Вдоль профильной линии до репера №22 оседания происходят умеренно, а от данного репера наблюдается резкое изменение значения оседания земной поверхности. Максимальное оседание, полученное с помощью нормативного метода составляет 1,9 м, а максимальное измеренное оседание равно 2,7 м. Разница между максимальными оседаниями имеет значение 0,8 м. Максимальная разница наблюдается в зонах точки №7 и №22 составляет 1,0 м, что по отношению к расчетному максимальному оседанию составляет 53%. На рис. 2а приведено отклонение оседаний земной поверхности между измеренными и рассчитанными данными. Определенной закономерности отклонений оседаний не наблюдается. На краевых частях отклонения выходят на отметку 0 м. Максимальные отклонения оседаний наблюдаются над центром лавы и за её пределами в диапазоне 100-200 м по профильной линии, и составляют около 0,9 м. Абсолютный разброс отклонений оседаний составляет 180 мм. На рис. 2б приведено статистическое распределение отклонений измеренных оседаний от расчетных. Величина разброса при моде 0 мм в большую сторону составляет 100 мм и в меньшую сторону -100 мм. Для установления закона распределения данных недостаточно (таблица 1), однако симметричность гистограммы и её вид позволяют сделать предположение о том, что такое распределение может согласоваться с нормальным законом.
На рис. 3 приведены наклоны земной поверхности, образованные после обработки рис. 1. Как видно из графиков, наклоны, полученные с помощью нормативного метода (расчетные) имеют значения в переделах 10*10-3 в обе стороны относительно оси, а измеренные наклоны достигают 25*10-3. Разница между максимальными наклонами имеет значение 15*10-3. Максимальная разница между значениями наклонов наблюдается на 550 м по профильной линии и составляет 21*10-3, что в процентном отношении составляет 210% по отношению к максимальному расчетному
В целом судя по виду экспериментальное распределение наклонов отражает основные закономерности, которые прогнозирует теоретическое распределение. В левой полумульде преобладают положительные наклоны, в правой отрицательные.
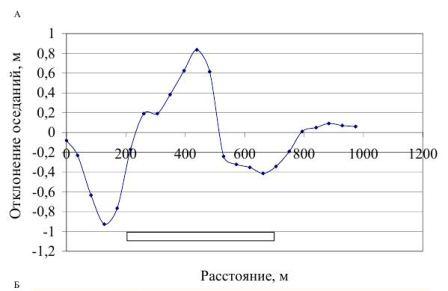
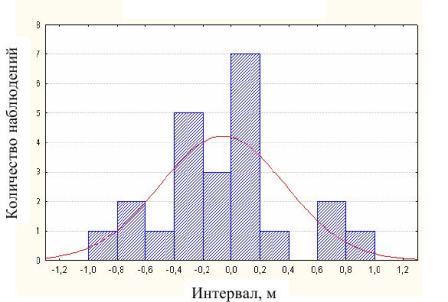
Рис. 2 – Распределение отклонений оседаний земной поверхности в главном вертикальном сечении мульды сдвижений между измеренными и рассчитанными данными
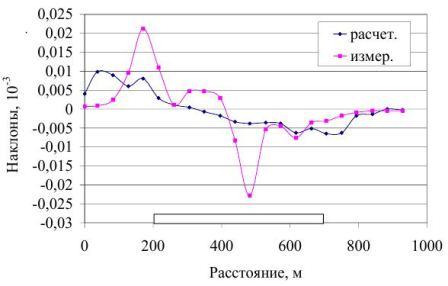
Рис. 3 – Сопоставление измеренных и рассчитанных наклонов, полученных по данным рис. 1
На рис. 4 представлены распределения отклонений наклонов земной поверхности между измеренными и рассчитанными данными. Распределение отклонений наклонов показанное на рис. 4а неравномерное. На краевых частях отклонения наклонов близки нулевому значению. Максимальные отклонения наклонов наблюдаются над центром лавы (20*10-3) и в пределе зоны 100 м по профильной линии (14*10-3). Абсолютные отклонения наклонов составляют 34*10-3. На рис. 4б приведено статистическое распределение отклонений между измеренными и расчетными наклонами. Для наклонов величина разброса при моде 0*10-3, в большую сторону составляет 20*10-3, а в меньшую сторону -15*10- 3 . Математическое ожидание равно нулю, разброс отклонений наклонов в обе стороны от матемачиского ожидания практически одинаков (таблица 2). Таким образом, гистограмма имеет симметричный вид. Статистическая проверка по критерию Колмогорова-Смирнова показала, что гистограмма согласуется с нормальным распределением.
Массив горных пород является неоднородным твердым телом с плохо предсказуемыми механическими свойствами. Продемонстрируем это утверждение гистограммами.
В работе [3] приведены результаты измерений модуля упругости одной и той же литологической разности осадочной породы. Гистограмма результатов испытаний приведена на рис. 6. Всего было испытано 19 образцов породы. Судя по экспериментальным данным, гистограмма имеет несимметричный вид. Величина разброса в большую сторону составляет 500 МПа, что в 2,85 раза больше моды равной 175 МПа. Эта разница достигает 285%, что является весьма существенным отклонением. Величина разброса в меньшую сторону составляет 50 МПа, что в 3,5 раза меньше моды, тогда разница составляет 350%.
Авторы данной статьи впервые обращают внимание на то, что распределение модуля упругости является несимметричным. В работах НГУ (Днепропетровск) показано, что логнормальное распределение хорошо описывает разброс предела прочности горной породы на одноосное сжатие [5]. В дальнейшем эту закономерность планируется проверить и для модуля упругости осадочной породы.
Причинами разброса деформационных и прочностных свойств является следующее: 1) погрешность испытаний на прессе в лабораторных условиях, которая возникает из-за непараллельности граней, непостоянства Рис. 6 – Статистическое распределение значений модуля деформации для скального массива [3] условия контакта, скорости нагружения образцов и т.д. В настоящее время существуют стандарты, которые позволяют снизить этот разброс менее чем на ±30%. 2) неопределенность термодинамического состояния образца при его извлечении из массива горных пород и транспортировки в лабораторию, а также условия хранения образца до момента испытания. Главными термодинамическими и физическими параметрами, которые вносят существенную погрешность в разброс физико-механических свойств являются температура, давление, влажность и др. Даже при больших затратах труда и средств исследователи не могут обеспечить температуру и влажность образца идентичные тем, которые были в массиве. 3) при переходе от образца к массиву необходимо свойства образца корректировать с учетом масштабного эффекта, величина которого может изменяться в несколько раз в зависимости от параметров трещиноватости массива. Так согласно В. Виттке среднее значение величины модуля деформации в массиве ниже значения, полученного для образцов в лаборатории в 3,3 раза.
Такое различие в значениях модулей деформации отчетливо демонстрирует влияние поверхностей раздела на деформируемость массива [3]. Другими словами трещиноватость массива вносит значительный вклад в разброс модуля деформации
Важно подчеркнуть, что масштабный эффект оказывает фундаментальное влияние на величину неопределенности прочностных и деформационных свойств массива горных пород. Так от первых двух факторов (погрешности испытаний в лаборатории и изменение термодинамических условий испытаний) можно избавиться путем проведения испытаний в натурных условиях. Для этого применяются специальные методики прямых испытаний в скважинах, специально оборудованных камерах, или используют методы косвенной оценки механических характеристик массива горных пород, например геофизическими методами. Однако естественная вариация параметров трещиноватости неизбежно вносит свой вклад в неопределенность результатов испытаний, величина которой остается весьма высокой.
На рис. 7 показано распределение фактора устойчивости массива горных пород. Определение фактора устойчивости массива вокруг горных выработок является одной из важнейших задач геомеханики [4]. Как видно устойчивые состояния имеют значения большие, чем критическая величина, а неустойчивые состояния, наоборот принимают меньшие значения по сравнению с критическим. На рис. 8 изображено совместно гистограммы устойчивых и неустойчивых состояний пород, на котором видна зона их наложения. Величина фактора устойчивости при этом определялась по классификации ARMPS [6].
Эта классификация основана на учете прочности пород в образце, густоты неоднородностей, количества систем трещин. Типичными параметрами трещиноватости является шероховатости краев, вид заполнителя, обводненность трещин и т.д. Чем выше плотность трещин, тем меньше устойчивость массива в целом. Все эти показатели имеют стохастическую природу. Важно, что параметры крепления охраны и поддержания горной выработки выбираются проектировщиками так, чтобы обеспечить фактическую величину критерия устойчивости не более чем 0,6-0,8 критической величины.
Для построения данных гистограмм значения каждой конкретной точки нормировалось относительно значения критической величины, и по полученным результатам строились гистограммы.
На рис. 9 изображено отношение между пределом прочности на одноосное сжатие и контактной прочностью, которое является исходными данными для построения гистограммы, приведенной на рис. 10. Анализируя гистограмму, можно сказать, что величина разброса контактной прочности при моде 4000 фут/дюйм2 составляет 550% в большую сторону и 200% в меньшую сторону. Гистограмма фактических данных не противоречит логнормальному закону, а разброс фактических и теоретических показателей прочности горной породы объясняется стохастической природой прочности твердого тела.

Рис. 9 - Связь между пределом прочности на одноосное сжатие и контактной прочностью для сланца [4]
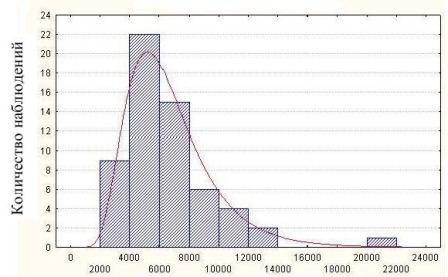
Рис. 10 - Распределение величин предела прочности в пределах интервала контактной прочности 200-300
сдвижения подрабатываемой толщи, имеют весьма большой разброс, распределения которого не симметричны и в большинстве случаев не противоречат логнормальному закону. Амплитуды разброса в таких случаях составляют от 285 до 550% в большую сторону и от 200 до 350% в меньшую сторону по отношению к моде этого показателя. В сумме разброс изменяется от 485 до 900%. Надо полагать, что такой разброс показателей должен существенно отразиться на разбросе оседаний и деформаций земной поверхности относительно от расчетного детерминированного уровня.
Для того чтобы исследовать, как разброс показателей влияет на процесс сдвижения необходимо выбрать подходящую геомеханическую модель. Для решения подобных задач чаще всего, используют метод конечных элементов, метод конечных разностей, метод граничных элементов, метод дискретных элементов. На сегодняшний день в подавляющем большинстве случаев исследователи использовали данные методы только для получения детерминированных оценок величин оседаний и деформаций земной поверхности [7-13]. Во всех случаях достоверность результатов прогноза проверяется путем сравнения расчетных показателей сдвижений с измеренными фактическими в натурных условиях. При этом авторы как правило не указывают какими причинами обусловлены эти отклонения. Хотя подразумевается, что эти причины имеют случайную природу. Новизной в данной работе является то, что метод конечных элементов (МКЭ) впервые применяется для исследования влияния стохастических факторов на случайный разброс параметров сдвижений.
Параметры деформационных и прочностных свойств реального массива горных пород определить точно невозможно. Основными причинами естественного случайного разброса величин модуля упругости, коэффициента Пуассона, сцепления и угла внутреннего трения массива горных пород является следующее:
1) погрешность испытаний;
2) неопределенность термодинамического состояния образца при его извлечении из массива горных пород и транспортировки в лабораторию, а также условия хранения образца до момента испытания;
3) масштабный фактор, который вносит максимальную неопределенность в прочностные и деформационные показатели массива горных пород.
С помощью стохастического численного моделирования на базовой модели метода конечных элементов установлены закономерности случайного разброса возможных величин оседаний земной поверхности над одиночным выработанным пространством. При этом показано, что несмотря на то, что средние оседания на границе мульды сдвижений равны нулю, величина разброса этих оседаний остается на уровне 25% от максимальных оседаний в центре мульды сдвижений.
Доказано, что прочностные показатели массива горных пород вносят основной вклад в разброс величин оседаний. При этом амплитуда разброса возможных оседаний в центре мульды всегда больше чем размах отклонений возможных оседаний на границе мульды. При вариации деформационных свойств массива горных пород амплитуда разброса возможных оседаний в центре мульды больше размаха возможных отклонений на границе мульды только в 2-3 раза, тогда как при вариации прочностных показателей массива горных пород указанные амплитуды разнятся на порядок.
Установлено, что разброс возможных величин оседаний ΔS согласуется с нормальным законом распределения случайной величины, а границы доверительного интервала разброса имеют S- образную форму вдоль мульды сдвижений и с надежностью 99% описываются экспоненциальной эмпирической зависимостью ΔS = ±0,51exp(-x2/0,22)+0,25, где х означает расстояние от центра мульды в метрах.
На основании установленной зависимости амплитуды разброса возможных величин оседаний вдоль мульды сдвижений предложена усовершенствованная методика определения расчетных оседаний путем введения поправки в ожидаемые величины сдвижений в виде двустороннего разброса вместо использования одностороннего коэффициента перегрузки. Такой подход повышает надежность определения величин оседаний и деформаций земной поверхности при ее подработке длинными очистными забоями.